- Угловая скорость 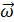 и угловое ускорение
и угловое ускорение 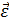 , их связь с линейными характеристиками.
, их связь с линейными характеристиками.
При вращательном движении вокруг неподвижной оси угловая скорость и угловое ускорение определяются формулами

где Т – период вращения, п – линейная частота вращения, т. е. число оборотов в единицу времени.
Модуль угловой скорости ω связан с модулем V линейной скорости точки соотношением
V = ωR
где R – расстояние от точки до оси вращения.
Тангенциальное и нормальное ускорения могут быть выражены в виде

- Момент силы и момент импульса. Момент инерции тела относительно закрепленной оси вращения.
Момент силы относительно оси вращения определяется как
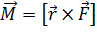
или модуль момента силы
M = rFsinα,
где α – угол между радиус-вектором, проведенным от оси вращения к точке приложения силы, и вектором силы.
Момент импульса относительно оси вращения для материальной точки определяется как 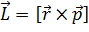 , а для абсолютно твердого тела –
, а для абсолютно твердого тела – 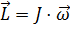
Момент инерции материальной точки определяется следующим образом:
J = mr2,
где m – масса движущейся точки, r – кратчайшее расстояние от точки до оси вращения.
Моменты инерции некоторых тел массой m относительно оси, проходящей через центр масс:
а) тонкого стержня длиной l относительно оси, перпендикулярной стержню и проходящей через его середину, –
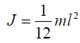
б) обруча (тонкостенного цилиндра) радиуса R относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра), –
J = mr2
в) диска радиуса R относительно оси, перпендикулярной плоскости диска и проходящей через его центр, –
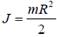
г) шара радиуса R относительно оси, проходящей через центр шара, –
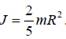
Теорема Штейнера
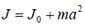
где J 0 – момент инерции тела относительно оси, проходящей через центр тяжести тела; а – величина параллельного смещения оси вращения.
Основной закон динамики вращательного движения:
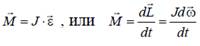
 2020-06-30
2020-06-30 102
102








