Как читаются формулы сокращенного умножения?

Г.

 

Раздел 13. Итоговое повторение курса математики

 

Тема 13.2. Решение примеров на применение тождеств сокращенного умножения

Тождество — это равенство верное при любых допустимых значениях входящих в его состав переменных. Всякую замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения.

Формулы сокращенного умножения:

1)   - Разность квадратов.

2) 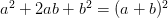  - Квадрат суммы.

3) 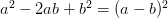  - Квадрат разности.

4) 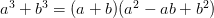  - Сумма кубов.

5)   - Разность кубов.

6)  - Куб суммы.

7)  - Куб разности.

8)  - Квадрат суммы трех чисел.

Перед вами базовый школьный комплект формул, изучаемый в 7 классе по всем программам. Наибольшая доля задач в учебниках приходится на применение первых трех формул.

Трехчлены: 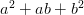и  называются неполными квадратами суммы и разности соответственно

Примите к сведению, что названия всех формул даются по самой короткой их части. Например, в формуле разность квадратов это левая часть, а в формуле квадрат суммы — правая. В начале названия формулы указывается последнее действие в этой короткой части. Например, в формуле разность квадратов – это разность, а в формуле квадрат суммы — это квадрат.

Если в последней формуле поставить знак минус, например перед b или c (или сразу оба знака), то в правой части знак минус появится перед тем удвоенным произведением, которое эту букву содержит (или два минуса дадут снова плюс).

Другие полезные алгебраические тождества:

 - выражение суммы квадратов двух чисел через их сумму.

 - выражение суммы квадратов двух чисел через их разность.

Как читаются формулы сокращенного умножения?

Чтобы рассказать решение примера, в котором были использованы формулы сокращенного умножения, нужно знать, как эти формулы читаются. Дадим соответствующие формулировки.

Сначала разберемся с принципом чтения формул сокращенного умножения. Это удобнее всего сделать, рассмотрев любую и них, например, первую формулу квадрата суммы вида: (a+b)²=a²+2·a·b+b².

В левой ее части находится выражение: (a+b)², которое представляет собой квадрат суммы двух выражений a и b, оно так и читается (отсюда понятно и название формулы). Дальше стоит знак равно, он и произносится как равно. В правой части формулы расположена сумма трех слагаемых: a², 2·a·b и b². a² и b² – это квадраты первого и второго выражений соответственно, а 2·a·b читается как удвоенное произведение выражений a и b, слово «удвоенное» отвечает числовому коэффициенту 2. Осталось соединить все эти рассуждения в одно предложение, которое будет ответом на вопрос, как читается формула квадрата суммы.

Итак, квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения первого и второго выражений и квадрата второго выражения.

Аналогично читаются и остальные фсу.

Так квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения. Эта формулировка второй фсу вида: (a−b)²=a²−2·a·b+b².

Дальше читаем формулу (a+b)³=a³+3·a²·b+3·a·b²+b³. Куб суммы двух выражений a и b равен сумме куба первого выражения, утроенного произведения квадрата первого выражения на второе, утроенного произведения первого выражения на квадрат второго и куба второго выражения.

Аналогично читается и формула куба разности: (a−b)³=a³−3·a²·b+3·a·b²−b³. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого на квадрат второго выражения минус куб второго выражения.

Переходим к чтению пятой по списку формулы сокращенного выражения: (a−b)·(a+b)=a²−b². Произведение разности двух выражений и их суммы равно разности квадратов первого и второго выражений.

А для удобства чтения шестой и, последней, седьмой ФСУ используют термины «неполный квадрат суммы» и «неполный квадрат разности» выражений a и b, которыми называют выражения: a²+a·b+b² и a²−a·b+b² соответственно. (В свою очередь выражения: a²+2·a·b+b² и a²−2·a·b+b² называют полным квадратом суммы и разности соответственно.)

Итак, произведение суммы двух выражений на их неполный квадрат разности равно сумме кубов этих выражений. Так читается формула: (a+b)·(a²−a·b+b²)=a³+b³. И произведение разности двух выражений на неполный квадрат их суммы равен разности кубов этих выражений, этому утверждению отвечает формула сокращенного умножения вида (a−b)·(a²+a·b+b²)=a³−b³.

Задача 1. Упростите выражение: 9· y −(1+3· y)².

Решение: В данном выражении возведение в квадрат можно выполнить сокращенно, имеем: 9· y −(1+3· y)²=9· y −(12+2·1·3· y +(3· y)²). Остается лишь раскрыть скобки и привести подобные члены: 9· y −(12+2·1·3·y+(3· y)²)=9· y −1−6· y −9· y ²=3· y −1−9· y ².

Ответ: 9· y −(1+3· y)²=3· y −1−9· y ².

Тождества сокращенного умножения с переставленными частями позволяют представлять выражения в виде степеней или произведений, в частности, выполнять разложение многочленов на множители. Это очень полезно, к примеру, при сокращении алгебраических дробей.

Задача 2. Сократите дробь:

.

Решение: В числителе выражение представляет собой разность кубов двух выражений: 2· x и z ², а в знаменателе – разность квадратов этих выражений. После применения соответствующих формул исходная дробь примет вид.

.

Теперь можно сократить одинаковые множители в числителе и знаменателе: .

Оформим все решение кратко:

Ответ: .

Формулы сокращенного умножения иногда позволяют рационально вычислять значения выражений. В качестве примера покажем, как можно возвести число 79 в квадрат с помощью формулы квадрата разности: 792=(80−1)2=802−2·80·1+12=6 400−160+1=6 241. Такой подход позволяет выполнять подобные вычисления даже устно.

В заключение скажем еще про одно важное преобразование – выделение квадрата двучлена, в основе которого лежит формула сокращенного умножения квадрат суммы. Например, выражение 4·x2+4·x−3 может быть преобразовано к виду (2·x)2+2·2·x·1+12−4, и первые три слагаемых заменяются с использованием формулы квадратом суммы. Так что выражение принимает вид (2·x+1)2−4. Подобные преобразования широко используются, например, при интегрировании.

Задача 3. Упростите выражение: (2 x ³ – 5 z)(2 x ³ + 5 z).

Решение: Воспользуемся формулой разности квадратов, получим: (2 x ³ – 5 z) (2 x ³ + 5 z) = (2 x ³)² – (5 z)² = 4 x ⁶ – 25 z ².

Ответ: 4 x ⁶ – 25 z ².

Задача 4. Упростите выражение:

а)(х – 5)² + 2 х (х – 3) = х ² – 10 х +25+         б) (2а – 5)² – (5а – 2)² = ((2а -5) + (5а – 2))·                                                   

+ 2 х ²-6 х = 3 х ² – 16 х +25.                                       ·((2а -5) – (5а – 2)) = (2а -5+5а -2)(2а-5-

                                                                  5а+2)=(7а-7)(-3а-3)=- 21а²-21а+21а+21

                =21-21а².                                                                     

Задача 5. Решите уравнение:

а) (х – 7)² + 3 =(х – 2)(х + 2).                               б) (2 х – 3)² – (7 – 2 х)² =2.

Ответ: х = 4.                                                         Ответ: х = 2 .

Задача 6. Преобразуй дробь 2 x +2 таким образом, чтобы в знаменателе было 3 x ²−12.

Решение:

1. Чтобы понять, как расширить дробь 2 x +2, выражение 3 x ²−12 раскладываем на множители:

3 x ²−12=3(x ²−4)=3(x −2)(x +2).

2. Сравниваем полученное выражение со знаменателем дроби x +2 и делаем вывод, что дополнительным множителем этой дроби является 3(x −2).

.

Задача 7. Упрости выражение 2 x ³+166 x ²−12 x +24.

Решение:

1. В числителе за скобки выносим общий множитель 2, а в знаменателе – общий множитель 6: 2 x ³+166 x ²−12 x +24=2(x ³+8)6(x ²−2 x +4).

2. Выражение x ³+8 раскладываем на множители, используя формулу суммы кубов, затем дробь сокращаем.

.