Федеральное государственное образовательное бюджетное учреждение
Высшего образования
«ФИНАН
«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ»
Департамент анализа данных, принятия решений и финансовых технологий
С.А.Зададаев
Задачи линейной оптимизации (RStudio)
Учебно-методические рекомендации для проведения
семинара №35 по компьютерному практикуму
Для бакалавров направления 38.03.01 «Экономика»
Москва 2018
Задачи линейной оптимизации (RStudio)
Последний раздел нашего практикума по R посвящен решению задач линейной оптимизации.
В идеале было бы хорошо заранее разобраться и прорешать несколько типов таких задач чисто аналитически. Это помогло бы не только понять основную идею решения таких задач, но и ощутить всю вычислительную мощь с одновременной простотой используемых команд в R.
Внимательно изучите каждый комментарий к строчкам приводимого кода. Для желающих основательно разобраться в линейном программировании и понять детали его экономического и физического смысла в конце раздела приведены ссылки на соответствующую литературу [1], [2].
Задание 1. Решить стандартную задачу линейного программирования


P.S. Задача заимствована из пособия [1] (пример 1.1 задача о костюмах, стр. 12)
Решение. Разобьем решение задачи линейного программирования на несколько этапов.
Задание задачи линейного программирования. Загружаем пакет lpSolveAPI из репозитория CRAN и отрабатываем следующий ниже код R.
При написании кода на R здесь и далее мы будем иногда выделять литеру "l" курсивом: " l ", чтобы не перепутать ее с единицей. При копировании такого текста в RStudio форматирование курсивом пропадет.
library(l pSolveAPI) # Активируем библиотеку линейного программирования
M <- make. l p(ncol = 2) # Объявляем количество неотрицательных переменных в M
name. l p(M, "Example") # Объявляем название "Example" для задачи (модели) М
colnames(M) <- c("X1", "X2") # Объявляем названия переменных в модели М
l p.control(M, sense = "max")$sense # Объявляем задачу на максимум модели М
set.objfn(M, c(10, 20)) # Задаем целевую функцию: f = 10*X1 + 20*X2 для модели М
add.constraint(M, c(1, 3.5), "<=", 350) # Задаем ограничение: 1*X1+3.5*X2 <= 350 для М
add.constraint(M, c(2, 0.5), "<=", 240) # Аналогично
add.constraint(M, c(1, 1), "<=", 150) # Аналогично
add.constraint(M, c(0, 1), ">=", 60) # Аналогично
rownames(M) <- c("A", "B", "C", "D") # Называем ограничения в модели М
M # Смотрим какая модель M в итоге получилась / можно print(M)
Запускаем введенный код на компиляцию с результатом:
> M # Смотрим какая модель M в итоге получилась / можно print(M)
Model name: Example
X1 X2
Maximize 10 20
A 1 3.5 <= 350
B 2 0.5 <= 240
C 1 1 <= 150
D 0 1 >= 60
Kind Std Std # тип – стандартнаяType Real Real # переменные – вещественнозначные, double
Upper Inf Inf # верхние границы изменения переменных
Lower 0 0 # нижние границы изменения переменных
Решение задачи линейного программирования. Далее решаем составленную задачу линейного программирования M:
solve. l pExtPtr(M) # Если 0, то ошибок нет – достигнуто оптимальное решение
get.variables(M) # Оптимальный план
get.objective(M) # Достигнутый max
> solve.lpExtPtr(M) # Если 0, то ошибок нет – достигнуто оптимальное решение[1] 0> get.variables(M)[1] 70 80 # Оптимальные значения переменных X1 и X2 в модели М> get.objective(M)[1] 2300 # Значение максимума целевой функции f в модели МРазумеется, можно сохранить полученное решение задачи M в соответствующие переменные:
X1.opt <- get.variables(M)[1]; X1.opt # Оптимальное значение для X1
X2.opt <- get.variab l es(M)[2]; X2.opt # Оптимальное значение для X2
f.max <- get.objective(M); f.max # Значение целевой функции на оптимальном решении
Здесь также могут быть полезны следующие дополнительные возможности по анализу характера полученного оптимального решения.
Оценка дефицита ресурсов:
# Значения правых частей неравенств системы:
b <- get.constr.value(M); b # Изначально заданные в системе неравенства
b.opt <- get.constraints(M); b.opt # Достигнутые значения на оптимальном решении
round(abs(b - b.opt), 10) # Строка дефицита (исчерпанность) ресурсов
> b <- get.constr.value(M); b # Изначально заданные в системе неравенств[1] 350 240 150 60> b.opt <- get.constraints(M); b.opt # Достигнутые на оптимальном решении[1] 350 180 150 80> round(abs(b - b.opt), 10) # Строка дефицита ресурсов[1] 0 60 0 20
Оценка устойчивости коэффициентов целевой функции:
# Минимальные и максимальные коэфф. в целевой функции, сохраняющие оптимальность:
min <- get.sensitivity.obj(M)$objfrom; min
max <- get.sensitivity.obj(M)$objtill; max
# Диапазоны коэффициентов целевой функции, сохраняющие оптимальность:
cbind(min, max) # i -ая строка – это диапазон устойчивости для i -ого коэффициента
> min <- get.sensitivity.obj(M)$objfrom; min[1] 5.714286 10.000000> max <- get.sensitivity.obj(M)$objtill; max[1] 20 35> cbind(min, max) # i-ая строка – диапазон устойчивости для i-ого коэффициента min max[1,] 5.714286 20 # диапазон устойчивости оптимальности для 1-ого коэфф.[2,] 10.000000 35 # диапазон устойчивости оптимальности для 2-ого коэфф.Решение двойственной к M задачи:
get.sensitivity.rhs(M)$duals # Оптимальный план двойственной задачи
# Минимальные и максимальные коэфф. в целевой функции, сохраняющие оптимальность:
min.dual <- get.sensitivity.rhs(M)$dua l sfrom; min.dual
max.dual <- get.sensitivity.rhs(M)$dua l still; max.dual
# Диапазоны коэффициентов целевой функции, сохраняющие оптимальность:
cbind(min.dual, max.dual) # i -ая строка – это диапазон устойчивости для i -ого коэффициента
> get.sensitivity.rhs(M)$duals # Оптимальный план двойственной задачи (Y1, Y2, Y3 и Y4)
[1] 4 0 6 0 0 0
> min.dual <- get.sensitivity.rhs(M)$dualsfrom; min.dual
[1] 3e+02 -1e+30 1e+02 -1e+30 -1e+30 -1e+30
> max.dual <- get.sensitivity.rhs(M)$dualstill; max.dual
[1] 5.250000e+02 1.000000e+30 1.730769e+02 1.000000e+30 1.000000e+30 1.000000e+30
> cbind(min.dual, max.dual) # i-ая строка – это диапазон устойчивости для i-ого коэффициента
min.dual max.dual
[1,] 3e+02 5.250000e+02
[2,] -1e+30 1.000000e+30
[3,] 1e+02 1.730769e+02
[4,] -1e+30 1.000000e+30
[5,] -1e+30 1.000000e+30
[6,] -1e+30 1.000000e+30
Справка по возможным ошибкам:
?solve. l pExtPtr(M) # Вызов справки по ошибкам при решении задачи ЛП
0: "optimal solution found" – найдено оптимальное решение
1: "the model is sub-optimal" – модель не имеет оптимального решения
2: "the model is infeasible" – max/min не достижим (возможно область пуста, возможно область не является ограниченной)
3: "the model is unbounded" – max/min не достижим, т.к. область неограниченна
4: "the model is degenerate" – модель вырождена
5: "numerical failure encountered" – ошибка вычислений, обычно связана с противоречивыми добавками в модель на стадии ее повторной прогонки
6: "process aborted" – процесс прерван (возможно пользователем)
7: "timeout" – истекло время, отводимое на необходимые вычисления, вероятно произошло зацикливание между двумя опорными решениями
9: "the model was solved by presolve" – модель была решена на стадии выбора опорного решения (вероятно имеется в виду)
10: "the branch and bound routine failed" – разветвления границы области слишком нетипичны, возможно их очень много
11: "the branch and bound was stopped because of a break-at-first or break-at-value" – нахождение угловых точек было прервано из-за изменения модели между сеансами обращения к ее решению (вероятно имеется в виду)
12: "a feasible branch and bound solution was found" – найдено одно из возможных решений (вероятно имеется в виду)
13: "no feasible branch and bound solution was found" – не найдено ни одного опорного решения (вероятно имеется в виду).
Задание 2. Решить задачу линейного целочисленного программирования


Решение. Составим следующий ниже код на R.
Задание задачи линейного программирования (внимательно изучите комментарии к каждой строке):
M.Int <- make. l p(ncol = 4) # Объявляем количество неотрицательных переменных в M.Int
name. l p(M.Int, "Examp l e Int") # Объявляем название задачи для M.Int
colnames(M.Int) <- c("X1","X2","X3","X4") # Объявляем названия переменных в M.Int
l p.control(M.Int, sense = "min")$sense # Объявляем задачу на максимум модели M.Int
set.objfn(M.Int, c(4, 3, 5, 6)) # Задаем целевую функцию: f = 4*X1 + 2*X2 + 3*X3 + X4
# Задаем первое ограничение: 1*X1+1*X2+2*X3+3*X4 >= 100 для модели M.Int:
add.constraint(M.Int, c(1, 1, 2, 3), "=", 123)
add.constraint(M.Int, c(2, 1, 1, 0), "=", 471) # Аналогично
rownames(M.Int) <- c("A", "B") # Называем ограничения в модели M.Int
set.type(M.Int, c(1,2,3,4), "integer") # Указываем номера целых переменных
# Указываем диапазоны изменения всех четырех переменных, при этом
# l ower – вектор нижних границ переменных, upper – правых. Inf – символ бесконечности:
set.bounds(M.Int, l ower = с(-Inf, -Inf, -Inf, -Inf), upper = c(Inf, Inf, 300, 400))
M.Int # Смотрим какая модель M.Int в итоге получилась
Запускаем код на компиляцию с результатом:
> M.IntModel name: Example Int X1 X2 X3 X4 Minimize 4 3 5 6 A 1 1 2 3 = 123B 2 1 1 0 = 471Kind Std Std Std Std Type Int Int Int Int Upper Inf Inf 300 400 Lower -Inf -Inf -Inf -InfРешение задачи линейного программирования. Далее решим составленную задачу линейного программирования M.Int:
solve. l pExtPtr(M.Int) # Если 0, то ошибок нет – достигнуто оптимальное решение
get.variables(M.Int) # Оптимальный целочисленный план
get.objective(M.Int) # Достигнутый минимум
> solve.lpExtPtr(M.Int) [1] 0> get.variables(M.Int)[1] 84 3 300 -188> get.objective(M.Int)[1] 717Попробуйте прогнать тот же код, но без указания целочисленности решения, т.е. предварительно «заремируйте» строку символом хэша #:
# set.type(M.Int, c(1,2,3,4), "integer") # Указываем номера целых переменных
и сравните ответ
> solve.lpExtPtr(M.Int) [1] 0> get.variables(M.Int)[1] 85.5 0.0 300.0 -187.5> get.objective(M.Int)[1] 717с полученным ранее целочисленным вариантом.
Вопрос для отличников: Если сравнивать ответы для этих двух задач, то можно заметить что, хотя оптимальные планы задач и получились разными, значение целевой функции на оптимальных решениях одинаково 717. О чем это говорит?
Задание 3. Решить транспортную задачу закрытого типа
| Склады | Тарифы в магазин | Запасы складов | ||||
|
|
|
|
|
| ||
|
| 1 | 2 | 3 | 4 | 5 | 160 |
|
| 4 | 3 | 2 | 7 | 3 | 150 |
|
| 5 | 5 | 4 | 2 | 8 | 220 |
| Потребности магазинов | 140 | 90 | 100 | 50 | 150 |
|
Решение. Кратко напомним, что искомым оптимальным планом в транспортной задаче является матрица  , состоящая из чисел
, состоящая из чисел  – количества перевезенной продукции со склада
– количества перевезенной продукции со склада  в магазин
в магазин 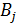 , а целевой функцией
, а целевой функцией  служит общая стоимость такой перевозки:
служит общая стоимость такой перевозки:
 .
.
Данная задача является задачей закрытого типа, т.к. сумма всех потребностей магазинов равна сумме всех запасов складов  . Поэтому, системы линейных ограничений по складам и по магазинам здесь выглядят в виде уравнений (точных равенств):
. Поэтому, системы линейных ограничений по складам и по магазинам здесь выглядят в виде уравнений (точных равенств):

Задание задачи линейного программирования. Можно было бы поступить аналогично предыдущим задачам линейного программирования, но мы воспользуемся другим специальным ресурсом – еще одной полезной библиотекой lpSolve.
library(l pSolve) # Активируем библиотеку линейного программирования
# В excel вводим матрицу тарифов и бросаем в буфер обмена.
# Читаем из буфера обмена данные в Data:
Data <- read.table("clipboard",h=FALSE,dec=",",sep = "\t") # Чтение из буфера обмена excel-формата
P <- as.matrix(Data); P # Объявляем таблицу Data матрицей P в R
См. рисунок 1.
Рис. 1

Далее вводим ограничения по запасам и потребностям, знаки ограничений (везде двойное равно ==) и объявляем транспортную задачу в терминах R:
SignA <- c("==", "==", "==") # Знаки в ограничниях складов Ai / а еще лучше: rep("==", 3)
SignB <- c("==", "==", "==", "==", "==") # Знаки в ограничниях магазинов Bj / rep("==", 5)
SumA <- c(160, 150, 220) # Запасы по складам Ai
SumB <- c(140, 90, 100, 50, 150) # Потребности магазинов Bj
# Записываем составленную транспортную задачу в переменную M.Tr:
M.Tr <- l p.transport(cost.mat = P, direction = "min",
row.signs = SignA, row.rhs = SumA,
col.signs = SignB, col.rhs = SumB)
Не забудьте набранный код отправить на компиляцию (Ctrl+Enter).
Решение транспортной задачи. Далее решаем составленную транспортную задачу M.Tr:
M.Tr$status # Eсли 0 - решение найдено
M.Tr$solution # Оптимальный план перевозок (матрица X)
M.Tr$objval # Минимальные суммарные транспортные расходы на перевозку
с результатом в консоли
> M.Tr$status # Eсли 0 - решение найдено[1] 0> M.Tr$solution # Оптимальный план перевозок (матрица X) [,1] [,2] [,3] [,4] [,5][1,] 140 20 0 0 0[2,] 0 0 0 0 150[3,] 0 70 100 50 0> M.Tr$objval # Минимальные суммарные транспортные расходы на перевозку[1] 1480Полный перечень произведенных вычислений по транспортной задаче M.Tr можно получить командой:
Str(M.Tr)
> str(M.Tr)List of 20 $ direction: int 0 $ rcount : int 3 $ ccount : int 5 $ costs : num [1:16] 0 1 4 5 2 3 5 3 2 4... $ rsigns : int [1:3] 3 3 3 $ rrhs : num [1:3] 160 150 220 $ csigns : int [1:5] 3 3 3 3 3 $ crhs : num [1:5] 140 90 100 50 150 $ objval : num 1480 $ int.count: int 15 $ integers: int [1:15] 1 2 3 4 5 6 7 8 9 10... $ solution: num [1:3, 1:5] 140 0 0 20 0 70 0 0 100 0... $ presolve: int 0 $ compute.sens: int 0 $ sens.coef.from: num [1:3, 1:5] 0 0 0 0 0 0 0 0 0 0... $ sens.coef.to: num [1:3, 1:5] 0 0 0 0 0 0 0 0 0 0... $ duals : num [1:3, 1:5] 0 0 0 0 0 0 0 0 0 0... $ duals.from: num [1:3, 1:5] 0 0 0 0 0 0 0 0 0 0... $ duals.to: num [1:3, 1:5] 0 0 0 0 0 0 0 0 0 0... $ status : int 0 - attr(*, "class")= chr "lp"часть из которых мы рассмотрели выше.
Замечание. Транспортная задача открытого типа будет отличаться от этой вместо равенств (==) нестрогими неравенствами (<=) в определении ограничений по суммарным запасам или потребностям, смотря каких больше. Подробнее см. [1].
 2020-07-01
2020-07-01 799
799
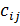 на перевозку со склада
на перевозку со склада