Основные определения теории графов

    При решении многих задач, встречающихся в компьютерных науках, математике, техниче­ских дисциплинах, часто возникает необходимость наглядного представления отно­шений между какими-либо объектами. Гра­фы — естественная модель для таких отношений. Они широко применяются для алгоритмического исследования структур дискретных систем. Рассмотрим основные определения.

    Граф – совокупность множества V вершин и множества Е связей между ними, которая обозначается G=(V,Е).

    Связь, имеющая направление, называется дугой, в противном случае – ребром.

    Граф с дугами называется ориентированным (или орграфом). На рис. 1,а показан ориентированный граф с множеством вершин V={1,2,3,4,5,6} и множеством ребер

E={(1,2),(2,4),(2,5),(4,1),(4,5),(5,4),(6,3),(6,6)}.

    Дуга, оба конца которой связаны с одной и той же вершиной, называется петлей (вершина 6).

    Граф, у которого все связи – ребра, называется неориентированным (или неорграфом). На рис. 1,б изображен неорграф с множеством вершин V={1,2,3,4,5,6} и множеством ребер E={(1,2),(1,5),(2,5),(3,6)}. Вершина называется изолированной, если она не связана с другими вершинами (не имеет смежных вершин) (вершина 4).

    Если граф имеет кратные ребра, т.е. несколько ребер, соединяющих одну и ту же пару вершин, то такие графы называются мультиграфами. На рис. 2 показаны мультиграфы: а – ориентированный мультиграф, б – неориентированный мультиграф. Граф есть псевдограф, если множество Е включает в себя ребра, дуги и петли, причем все они могут быть кратными. Псевдограф изображен на рис. 3.

       

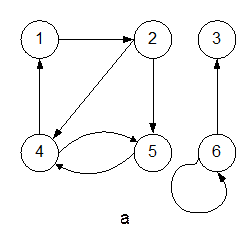
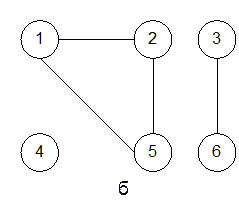
Рис. 1

                        

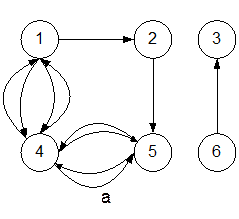
Рис. 2

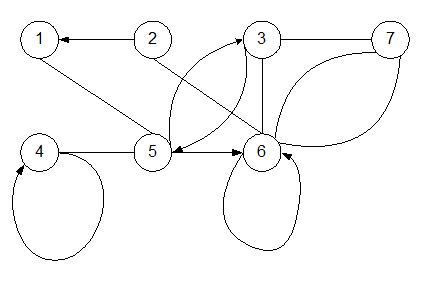
Рис. 3

    Про дугу (v,w) орграфаговорят также, что она выходит из вершины v и входит в вершину w. Например, на рис. 1,а имеется два ребра, выходящих из вершины 2 (ребра (2,4) и (2,5)), и одно, в нее входящее (ребро (1,2)). Про ребро (v,w) неорграфа говорят, что оно инцидентно вершинам v и w. Например, на рис. 1,б имеется два ребра, инцидентные вершине 2 (ребра (1,2) и (2,5))

    Если в графе G есть дуга (ребро) (V,Е), считают, что вершина V смежнаяс вершиной Е. Для неорграфов отношение смежности является симметричным, а для орграфов это необязательно. На рис. 1,а,б вершина 1 является смежной с вершиной 2, но только на рис. 1,б вершина 2 смежная с вершиной 1 (дуга (2,1) отсутствует в орграфе). Две вершины графа смежные, если они соединены ребром (дугой) (например, смежными являются вершины 2 и 5 на рис. 1,а и 1 и 5 рис. 1,б.

    Две различные дуги (ребра) смежные, если они имеют общую вершину. Например, смежными дугами на рис. 1,а являются дуги (1,2) и (2,5); cмежными ребрами, например, на рис. 1,б – ребра (1,2) и (1,5).

    Вершина v_i инцидентна дуге (ребру) E_ij, если она является началом или концом дуги (ребра). Например, вершина 2 рис. 1,а инцидентна трем дугам: (1,2), (2,4) и (2,5). А вершина 5 на рис. 1,б инцидентна ребрам (1,5) и (2,5).

    Дуга (ребро) E_ij инцидентна вершине v_i, если выходит из этой вершины. Например, дуга (1,2) на рис. 1,а инцидентна вершине 1. Ребро (2,5) на рис. 1,б инцидентно вершинам 2 и 5.

    Степенью вершины называется число инцидентных ей дуг (ребер). Для неорграфа сумма степеней вершины равна удвоенному числу его ребер. Например, для неорграфа на рис. 1,б степень вершины 2 равна 4. Для орграфа вводится понятие полустепени исхода (или исходящая степень) и полустепени захода (или входящая степень) вершины, что соответствует числу входящих и выходящих дуг. Сумма полустепеней называется степенью. Например, вершина 2 на рис. 1,а имеет полустепень исхода 2, полустепень захода 1 и степень 3.

    Путь длины k из вершины u в вершину v определяется как последовательность вершин (v₀,v₁,v₂,…,v_k), в которой v₀=u, v_k=v и
  (v_i-1,v_i) є Е для всех i=1,2,…,k. Таким образом, путь длины k состоит из k рёбер. Этот путь содержит вершины v₀,v₁,v₂,…,v_k и рёбра (v₀,v₁),(v₁,v₂),…, (v_k-1,v_k). Вершину v₀ называют началом пути, вершину vk — его кон­цом; говорят, что путь ведёт из v₀ в v_k. Если для данных вершин u и u' существует путь р из u в u ', то говорят, что вершина u' достижима из u по пути р.

    Путь называется простым, если все вершины в нём различны. Например, на рис. 1,а есть простой путь (1,2,5,4) длины 3, а также путь (2,5,4,5) той же длины, не являющийся простым.

    Определим путь между вершинами графа. Если v_i-1 ¹ v_j, то d(v_i) есть число ребер (дуг), содержащихся в кратчайшем по количеству ребер (дуг) маршруте, соединяющем указанные вершины. Тогда d(v_i,v_i)=0 для всех v_i. Для фиксированной вершины v_i целое число

R(v_j)=max{d(v_j,v_i)}, где v_i,v_j є Е соответствует расстоянию от v_i до вершины (или вершин), наиболее удаленной от v_i.

Например, для графа на рис. 4 подсчитаем величины d(v_i,v_j):

 

d(1,1)=0	d(2,1)=3	d(3,1)=3	d(4,1)=1	d(5,1)=1	d(6,1)=2
d(1,2)=3	d(2,2)=0	d(3,2)=1	d(4,2)=2	d(5,2)=3	d(6,2)=1
d(1,3)=3	d(2,3)=1	d(3,3)=0	d(4,3)=2	d(5,3)=3	d(6,3)=1
d(1,4)=1	d(2,4)=2	d(3,4)=2	d(4,4)=0	d(5,4)=1	d(6,4)=1
d(1,5)=1	d(2,5)=3	d(3,5)=3	d(4,5)=1	d(5,5)=0	d(6,5)=2
d(1,6)=2	d(2,6)=1	d(3,6)=1	d(4,6)=1	d(5,6)=2	d(6,6)=0

 

Теперь в каждом столбце определим наибольшее значение и получим значение R(v_i):

 

R(1)=3

R(2)=3

R(3)=3

R(4)=2

R(5)=3

R(6)=2

 

    Таким образом, наиболее удалены от 1-й вершины: 2–я и 3–я, от 2-й вершины: 1–я и 5–я, от 3-й вершины: 1–я и 5–я, от 4-й вершины: 2–я и 3–я, от 5-й вершины: 2–я и 3–я, от 4-й вершины: 1–я и 5–я.

    Величину R=min{R(v_i)}, где v_i є Е, называют радиусом связного графа, и считают вершину v_i центром графа, если R(v_i)=R. Граф может иметь несколько центров. Для графа на рис. 4 радиус равен двум, а центр графа – вершины 4 и 6.

    Диаметром D связного графа является величина

D=max{d(v_j,v_i)}, где v_j,v_i є Е.

Для графа на рис. 4 диаметр равен трем.

    Под средним диаметром графа понимают величину
Dcp=C/(N*(N-1)), где С – сумма кратчайших расстояний между всеми парами вершин графа, N – число вершин графа. Для графа на рис. 4 С=54, N=6, D=54/(6*5)=1.8.

    Подпуть пути р = (v₀,v₁,v₂,…,v_k) получится, если мы возьмём не­которое количество идущих подряд вершин этого пути, т.е. последовательность (v_i,v_i+1,…,v_j) при некоторых i, j, для которых
0 £ i £ j £ k.

    Циклом в орграфе называется путь, в котором на­чальная вершина совпадает с конечной и который содержит хотя бы одно ребро. Цикл (v₀,v₁,v₂,…,v_k) называется простым, если в нём нет одинаковых вершин (кроме первой и последней), т.е. если все вершины v₀,v₁,v₂,…,v_k различны. Ребро-цикл является циклом длины 1. Причем, считают тождественными циклы, отличающиеся сдвигом вдоль цикла: один и тот же цикл длины k может быть представлен k различными путями (в качестве начала и конца можно взять любую из k вершин). Например, на рис. 1,а пути (1,2,4,1), (2,4,1,2) и (4,1,2,4) пред­ставляют собой один и тот же цикл. Этот цикл является простым, в то время как цикл (1,2,4,5,4,1) таковым не является. На том же рисунке есть цикл (6,6), образованный единственным ребром-циклом (6,6). Орграф, не содержащий рёбер-циклов, называется простым.

    В неорграфе путь (v₀,v₁,v₂,…,v_k) называется (простым) цик­лом (контуром), если k ³ 3, (v₀ = v_k) и все вершины v₁,v₂,…,v_k различны. Например, на рис. 1,б имеется простой цикл (1,2,5,1).

    Обхват графа – длина кратчайшего цикла (контура). Например, для графа рис. 4 обхват равен 3.

Эйлеров цикл (контур) – это цикл (контур), проходящий через все ребра (дуги) по одному разу. Если каждая вершина графа имеет четную степень (полустепень исхода и захода), то граф имеет эйлеров цикл (контур). Граф на рис. 5 имеет эйлеров цикл: {1,2,3,6,4,5,1} длиной6.

    Граф, в котором нет циклов, называется ациклическим.

    Неорграф называется связным, если для любой пары вершин существует путь из одной в другую. Например, граф на рис. 4 – связный. Для неорграфа отношение «быть достижимым из» является отношением эквивалентности на множестве вершин. Классы эквивалентности называются связными компо­нентами графа. Например, на рис. 1,б имеются три связные компоненты: {1,2,5}, {3,6} и {4}. Неориентированный граф связный тогда и только тогда, когда он состоит из единственной связной компоненты. Несвязный граф состоит, по крайней мере, из двух компонент связности. Если после удаления вершины увеличивается число компонент связности, то это точка сочленения, ребро с таким же свойством – мост. Например, для графа на рис. 4 вершина 6 – точка сочленения, так как после ее удаления число компонент связности будет равно двум: {1,4,5} и {2,3}, а ребро {4,6} – мост.

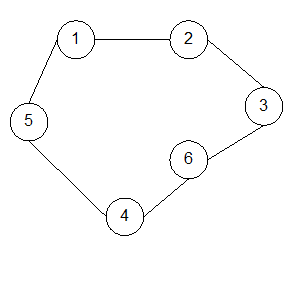
Рис. 4                                                   Рис. 5

 

    Вершинная связность графа – это наименьшее число вершин, удаление которых приводит к несвязному или тривиальному графу, т.е. графу из одних вершин. Реберная (дуговая) связность определяется как наименьшее количество ребер (дуг), удаление которых приводит к несвязному или тривиальному графу.

    Орграф называется сильно связным, ес­ли из любой его вершины достижима (по ориентированным путям) любая другая вершина. Любой орграф можно разбить на сильно связные компоненты, которые определяются как классы эквивалент­ности отношения «u достижимо из v и v достижимо из u». Орграф сильно связан тогда и только тогда, когда состоит из единственной сильно связной компоненты. Граф на рис. 1,а имеет три таких компоненты: {1,2,4,5}, {3} и {6}. Заметим, что вершины {3,6} не входят в одну сильно связную ком­поненту, так как 3 достижима из 6, но не наоборот.

    Два графа G = (V, Е) и G' = (V', Е') называются изоморфными, если существует взаимно однозначное соответствие
f: V ® V' между мно­жествами их вершин, при котором рёбрам одного графа соответствуют рёбра другого: (u,v) є E  тогда и только тогда, когда (f(u),f(v)) є Е'. Можно сказать, что изоморфные графы — это один и тот же граф, в котором вершины названы по-разному. На рис. 6 приведен пример двух изоморфных графов G и G' с множествами вершин V = {1, 2, 3, 4, 5, 6} и V = {и, v, w, х, у, z}. Функция f: V ® V', для которой f(1)=u, f(2)=v, f(3)=w, f(4)=x, f(5)=y, f(6)=z, явля­ется изоморфизмом. Напротив, графы на рис. 7 не изоморфны, хотя оба име­ют по 5 вершин и по 7 рёбер. Чтобы убедиться, что они не изоморфны, доста­точно отметить, что в графе G есть вершина степени 4 (это вершина 1), а в графе G' — еёнет.

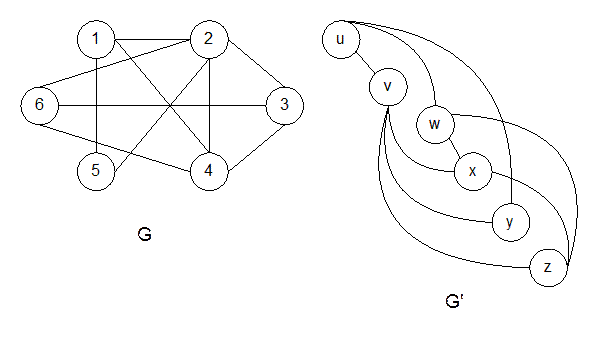
Рис. 6

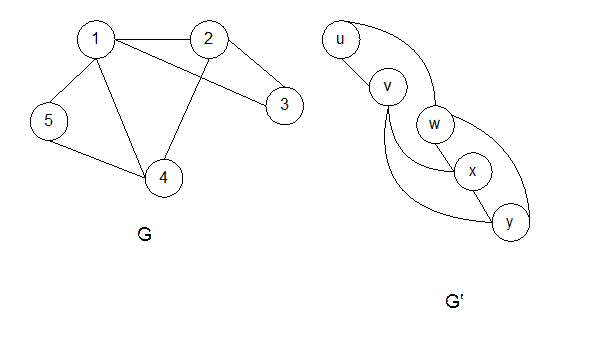
Рис. 7

    Граф G' = (V',E') называют подграфом графа G — (V,E), если Е' Í Е и V' Í V (в графе опущены некоторые вершины и инцидентные им ребра (дуги).

    Если в графе G = (V, Е) выбрать произвольное множество вершин V', то можно рассмотреть его подграф, состоящий из этих вершин и всех соединяющих их рёбер, т.е. граф G' = (V',E'), для которого

Е'= {(u,v) є E: u,v єV'}.

Этот подграф можно назвать ограничением графа G на множество вершин V'. Ограничение графа рис. 1,а на множество вершин {1,2,3,6} показано на рис. 8,а и имеет три ребра (1,2), (6,3), (6,6).

    Если в графе опущены некоторые ребра (дуги), а число вершин осталось прежним, то полученный граф — частичный. На рис. 8,б изображен частичный граф для графа рис. 1,б.

    Для любого неорграфа G можно рассмотреть его ориенти­рованный вариант, заменив каждое неориентированное ребро (u,v) на пару ориентированных дуг (u,v) на (v,u), идущих в противоположных направлениях. С другой стороны, для каждого орграфа можно рассмотреть его неориентированный вариант, забыв про ориентацию дуг, удалив ребра-циклы и соединив дуги (u,v) и (v,u) в одно неориентированное ребро (v,u). В орграфе соседом вершины u называют любую вершину, соединенную с ней дугой (в любую сторону); таким образом, v является соседом u тогда и только тогда, когда v смежно u или u смежно v. Для неорграфа выражения «v – сосед u» и «v – смежна с u» являются синонимами.

     

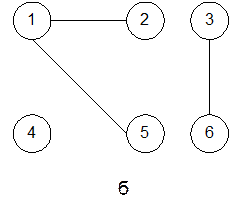
Рис. 8

 

    Цикломатическим числом графа без петель, состоящего из р компонентов связности, называется число V(G)=q-N*p, где q – число ребер графа. Оно определяет наименьшее число ребер, которое необходимо удалить из данного графа, чтобы получить граф без циклов. Цикломатическое число мультиграфа равно максимальному числу независимых циклов, в каждом из них содержится, по крайней мере, одно ребро, не входящее в другие циклы графа. Например, граф G на рис. 7 имеет N=5 (количество вершин графа), q=7 (число ребер графа), p=1 (число компонент связности, граф G – сильно связный), тогда V(G)=7-5*1=2.

    Некоторые виды графов имеют специальные названия. Полным графом называют неорграф, содержащий все возможные ребра для данного множества вершин (любая вершина смежна с любой другой). На рис. 9 граф G₁, является полным. Дерево – это связный граф без циклов. Очевидно, что для дерева справедливо N=q+1, каждое ребро (дуга) дерева – мост. На рис. 9 граф G₂ является деревом.

Рис. 9

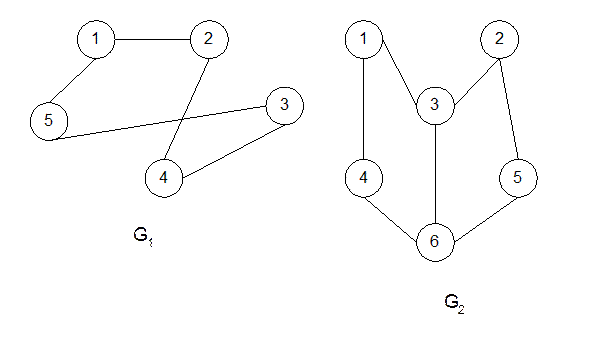
Рис. 10

 

    Если граф имеет вершины одинаковой степени (полустепени исхода и захода), то он регулярный. В нем каждая пара смежных вершин имеет одинаковое число соседей. Граф G₁ на рис. 10 является регулярным.

    Двудольный (бихроматический) граф – это граф, не содержащий циклов (контуров) нечетной длины. У такого графа множество вершин V можно разбить на две части V₁ и V₂ таким образом, что концы любого ребра оказываются в разных частях. Граф G₂ на рис. 10 является двудольным.

    Операция гомеоморфного сжатия заключается в замене двух ребер (дуг) одним, удалением вершины второй степени (полустепени исхода и захода, равной единице). На рис. 11,а показан граф после гомеоморфного сжатия графа G  рис. 6 (ребра (1,2) и (2,3) заменены ребром (1,3), а ребра (1,4) и (4,6) на ребро (1,6)). После повторного применения этой же операции получен граф, изображенный  на рис. 11,б. При этом ребра (1,3) и (3,4) заменены ребром (1,4).

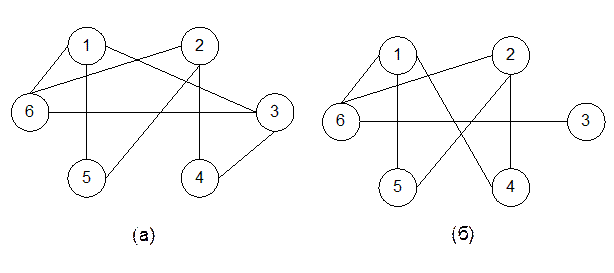
Рис. 11

 

Графом окрестности подмножества 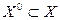  называют подграф, образованный вершинами 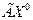, т.е. смежными с . Графом замкнутой окрестности подмножества 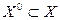 называют подграф, образованный вершинами .

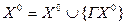    Иногда с ребрами (дугами) и (или) вершинами графа сопоставляются числа – вес ребра (дуги) и вес вершины. Такой граф является графом со взвешенными ребрами (дугами) и (или) вершинами.