Сложение гармонических колебаний
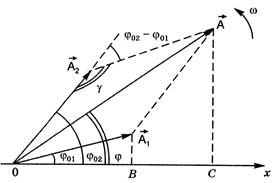 Пусть тело одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении, причем амплитуды и начальные фазы колебаний различны (А 1 ≠ А 2, φ01 ≠ φ02):
Пусть тело одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении, причем амплитуды и начальные фазы колебаний различны (А 1 ≠ А 2, φ01 ≠ φ02):
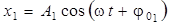 ,
, 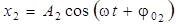 .
.
Результирующее движение, равное сумме колебаний х 1 и х 2, будет гармоническим колебанием той же циклической частоты ω:
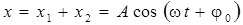 .
.

Биения – это колебания, которые возникают в результате сложения двух гармонических колебаний х1 и х2одного направления с близкими частотами (ω2, ω1 >> ∆ω = ω2 – ω1):
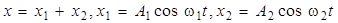 .
.
На рис. 11.4 приведены графики изменения амплитуды биения АБ и смещения х м. т. от времени. Метод биений применяют, например, для настройки музыкальных инструментов.
Билет 19
Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю:
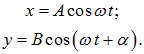
| (1.55) |
где 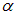 — разность фаз обоих колебаний. Найдем уравнение траектории колеблющейся материальной точки, то есть функцию
— разность фаз обоих колебаний. Найдем уравнение траектории колеблющейся материальной точки, то есть функцию 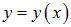 .
.
Рассмотрим сначала частные случаи. Пусть разность фаз равна нулю: 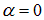 . Тогда
. Тогда
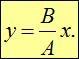
| (1.56) |
то есть траектория точки представляет собой прямую. Аналогичная траектория получится при колебаниях с разностью фаз 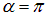
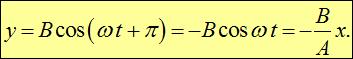
| (1.57) |
При разности фаз 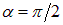 находим:
находим:
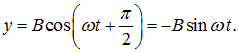
| (1.58) |
Из (1.58) и (1.55) следует уравнение эллипса:
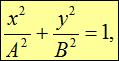
| (1.59) |
причем точка движется по часовой стрелке (для стандартного направления осей: ось ОХ — направо, ось ОУ — вверх). При разности фаз 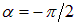 находим:
находим:
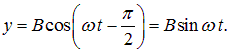
| (1.60) |
Это приводит к той же эллиптической траектории (1.59), только вращение в этом случае происходит против часовой стрелки.
Если амплитуды колебаний по осям х и у одинаковы (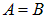 ), то из (1.59) получается круговая траектория.
), то из (1.59) получается круговая траектория.
В общем случае произвольной разности фаз 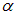 траектория также будет представлять собой эллипс, но с повернутыми осями (рис. 1.18).
траектория также будет представлять собой эллипс, но с повернутыми осями (рис. 1.18).
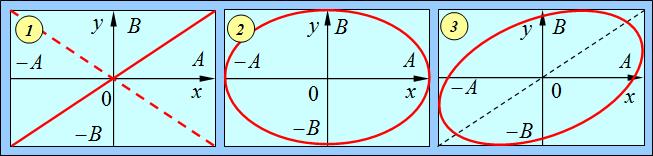
Рис. 1.18. Траектории материальной точки, колеблющейся с одинаковыми частотами
в перпендикулярных направлениях, при различных разностях фаз:
1 — 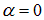 или
или 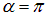 (штриховая линия); 3 —
(штриховая линия); 3 —  ; 2 —
; 2 — 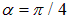
 2020-07-12
2020-07-12 233
233








