Алгоритмы к решению задач по теме: «Применение производной»

1. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 7; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [− 5; 2].

1.

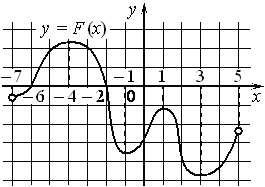
1.

1. На рисунке изображён график некоторой функции y=f(x) (два луча с общей начальной точкой).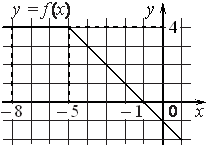

2. Пользуясь рисунком, вычислите F(− 1)−F(− 8), где F(x) — одна из первообразных функции f(x).

1.

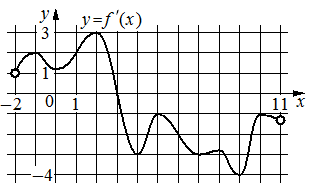
1. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 2 ; 11). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс
или совпадает с ней.

2.

1. С помощью производной мы находим мгновенную скорость и ускорение точки; строим касательную к графику функции; находим критические точки; промежутки возрастания, убывания и постоянства функции; точки экстремума; экстремумы функции; используем производную для исследования функции и построения ее графика; для решения «экстремальных задач»; для нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке. Почти все типы задач решаются с помощью алгоритмов.

• Алгоритм нахождения критических точек функции.

1. Найти область определения функции.

2. Найти производную функции.

3. Решить уравнение f '(х) = 0.

4. Выяснить, являются ли корни уравнения f '(х) = 0 внутренними точками определения функции.

5. Сделать вывод.

1. Пример 14. Найти критические точки функций.

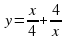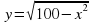2. а) б) в) .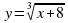

• Алгоритм нахождения промежутков возрастания и убывания функции.

1. Найти область определения функции и интервалы, на которых функция непрерывна.

2. Найти производную функции.

3. Найти критические точки: f '(х) = 0.

4. Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов. (Если на рассматриваемом интервале
f '(х) 0, то функция возрастает, а если f '(х)

1. Пример 15. Найти промежутки возрастания и убывания функции

2.

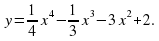
• Необходимое условие экстремума

1. В точках экстремума, производная функции равна нулю или не существует. Но не в каждой точке х₀, где f '(х₀) =0 или f '(х₀) не существует, будет экстремум.

• Достаточное условие экстремума

1. Если функция f (х) непрерывна в точке х₀ и производная f '(х) меняет знак в точке х_0, то х₀ – точка экстремума функции f (х).

2. Если в точке х₀ знак f '(х) меняется с «+» на «-», то х₀ – точка максимума.

3. Если в точке х₀ знак f '(х) меняется с «-» на «+», то х₀ – точка минимума.

4. Точки максимума и минимума называются точками экстремума. А значения функции в точках экстремума называются экстремумами функции.

• Алгоритм нахождения точек экстремума и экстремумов функций

1. Найти область определения.

2. Найти производную функции

3. Найти критические точки

4. Отметим критические точки на области определения и определим знак производной на каждом из полученных интервалов.

5. Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума.

.

Ответы отправить на почту mathetuka@yandex.ru