2020-08-05
59
Дисциплина: Математика
Семестр:2 Курс: 1
Направления: ИВТ, АТТПП,С, Э, ЭТТМИК
Преподаватель: Назаров С.А.
Вариант № 10
1. Вычислить неопределенный интеграл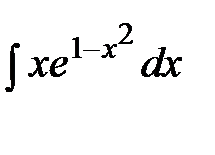 
2. Вычислить определенный интеграл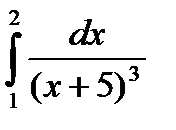 
3. Изменить порядок интегрирования: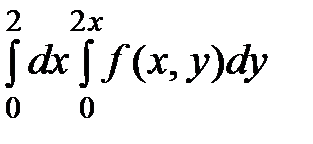 
.
4. Вычислить площадь плоской фигуры, ограниченной линиями:
у = х 2, у = 4х – 3;
5. Решить дифференциальное уравнение 1-го порядка
6. Решить дифференциальное уравнение 2-го порядка и задачу Коши
 ,
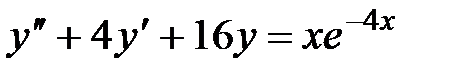| у(0) = 0, у¢(0) = 0 |
7. Проверить условия Коши-Римана
w = z2 + 2z -1. (z=x+iy)
8. Исследовать сходимость ряда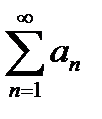 
, 
= 
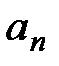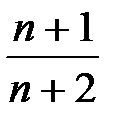
9. Найти область сходимости ряда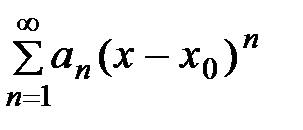 
, 
, х0 = 1.
10. Разложить функцию f (x) = cos(x2) в ряд Тейлора по степеням x
. Экзаменационная работа.
Дисциплина: Математика
Семестр:2 Курс: 1
Направления: ИВТ, АТТПП,С, Э, ЭТТМИК
Преподаватель: Назаров С.А.
Вариант № 11
1. Вычислить неопределенный интеграл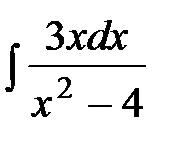 
2. Вычислить определенный интеграл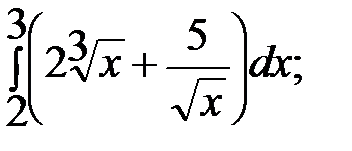 
3. Изменить порядок интегрирования: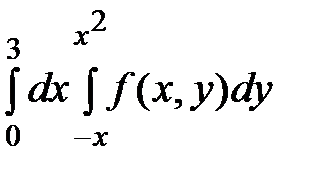 
.
4. Вычислить площадь плоской фигуры, ограниченной линиями:
|
|
|
4y = x2, x2 +2y = 0
5. Решить дифференциальное уравнение 1-го порядка
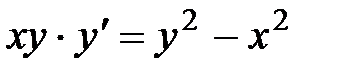
6. Решить дифференциальное уравнение 2-го порядка и задачу Коши
 ,
| у(0) = 0, у¢(0) = 1 |
7. Проверить условия Коши-Римана
w = z2 +2 z -1. (z=x+iy)
8. Исследовать сходимость ряда =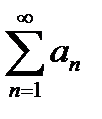 
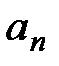9. Найти область сходимости ряда ,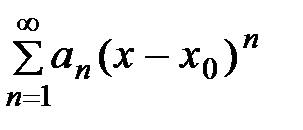 
, х0 = -2.
10. Разложить функцию f (x) = cos(x+1) в ряд Тейлора
. Экзаменационная работа.
Дисциплина: Математика
Семестр:2 Курс: 1
Направления: ИВТ, АТТПП,С, Э, ЭТТМИК
Преподаватель: Назаров С.А.
Вариант № 12
1. Вычислить неопределенный интеграл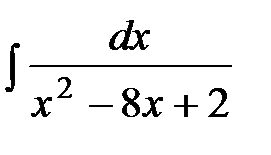 
2. Вычислить определенный интеграл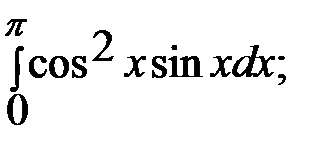 
3. Изменить порядок интегрирования: 
.
4. Вычислить площадь плоской фигуры, ограниченной линиями:
y = sinx, y = cosx и осью Oy;
5. Решить дифференциальное уравнение 1-го порядка
6. Решить дифференциальное уравнение 2-го порядка и задачу Коши
 ,
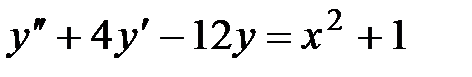| у(0) = 0, у¢(0) = 1 |
7. Записать комплексное число в алгебраической и тригонометрической форме
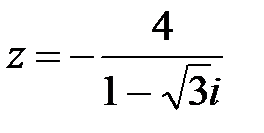
8. Исследовать сходимость ряда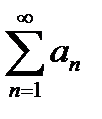 
9. Найти область сходимости ряда ,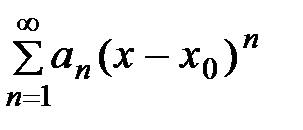 
, х0 = - 1
10. Разложить функцию f (x) = cos(4x) в ряд Тейлора
. Экзаменационная работа.
Дисциплина: Математика
Семестр:2 Курс: 1
Направления: ИВТ, АТТПП,С, Э, ЭТТМИК
Преподаватель: Назаров С.А.
Вариант № 13
1. Вычислить неопределенный интеграл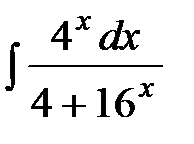 
2. Вычислить определенный интеграл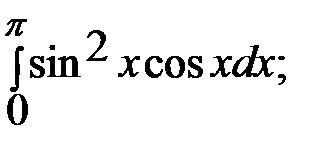 
3. Изменить порядок интегрирования: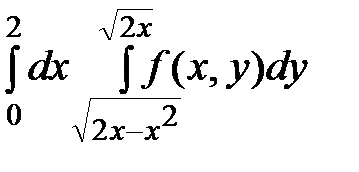 
.
4. Вычислить площадь плоской фигуры, ограниченной линиями:
| x2–9y = 0, x–3y+6 = 0 |
5. Решить дифференциальное уравнение 1-го порядка
6. Решить дифференциальное уравнение 2-го порядка и задачу Коши
 ,
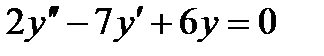| у(0) = 0, у¢(0) = -1 |
7. Записать комплексное число в алгебраической и тригонометрической форме
|
|
|
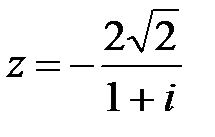
8. Исследовать сходимость ряда =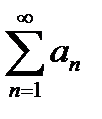 
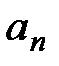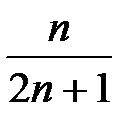
9. Найти область сходимости ряда , =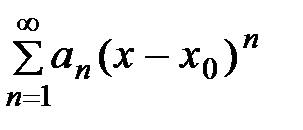 
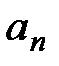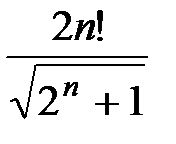, х0 = 0
10. Разложить функцию f (x) = sin(4x) в ряд Тейлора
. Экзаменационная работа.
Дисциплина: Математика
Семестр:2 Курс: 1
Направления: ИВТ, АТТПП,С, Э, ЭТТМИК
Преподаватель: Назаров С.А.
Вариант № 14
1. Вычислить неопределенный интеграл 
2. Вычислить определенный интеграл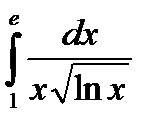 
3. Изменить порядок интегрирования: 
.
4. Вычислить площадь плоской фигуры, ограниченной линиями:
| y = 4x–x2, y = 0 |
5. Решить дифференциальное уравнение 1-го порядка
6. Решить дифференциальное уравнение 2-го порядка и задачу Коши
 ,
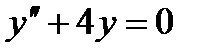| у(0) =  , у¢(0) =
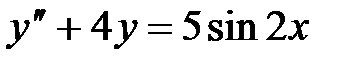| №20.  ,
| у(0) = , у¢(0) =
|
7. Записать комплексное число в алгебраической и тригонометрической форме
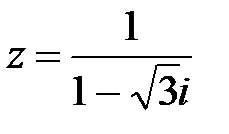
8. Исследовать сходимость ряда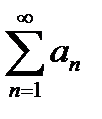
9. Найти область сходимости ряда 
, х0 = 0.
10. Разложить функцию f (x) = e2x в ряд Тейлора
. Экзаменационная работа:
Дисциплина: Математика
Семестр:2 Курс: 1
Направления: ИВТ, АТТПП,С, Э, ЭТТМИК
Преподаватель: Назаров С.А.
Вариант № 15
1. Вычислить неопределенный интеграл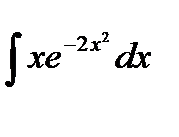 
2. Вычислить определенный интеграл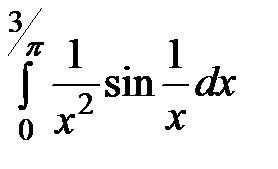 
3. Изменить порядок интегрирования: 
.
4. Вычислить площадь плоской фигуры, ограниченной линиями:
| ) y = lnx, y = 0, x =e |
5. Решить дифференциальное уравнение 1-го порядка
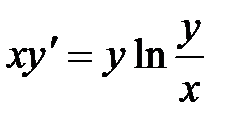
6. Решить дифференциальное уравнение 2-го порядка и задачу Коши
 ,
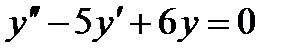| у(0) = 0, у¢(0) = 0 | №2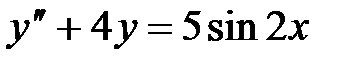0. ,
| у(0) = , у¢(0) =
|
7. Проверить условия Коши -Римана
w = 2z3 - zi. (z=x+iy)
8. Исследовать сходимость ряда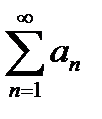 
= 
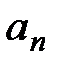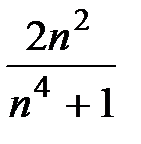
9. Найти область сходимости ряда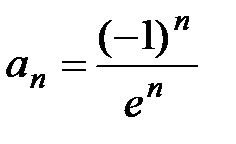 
, х0 = 0.
10. Разложить функцию f (x) = e-x в ряд Тейлора
