| Импульс. Закон сохранения импульса. | |
| При решении динамических задач необходимо знать какие силы действуют на тело, закон, позволяющий рассчитать конкретную силу. Цель: получить решение задачи механики исходя из начальных условий, не зная конкретного вида взаимодействия. | |
| Законы Ньютона в полученной ранее форме не позволяют решать задачи на движение тела с переменной массой и при скоростях, сравнимых со скоростью света. Цель: получить записи законов Ньютона в форме, справедливой для этих условий. | |
Импульс силы Векторная физическая величина, являющаяся мерой действия силы за некоторый промежуток времени. 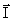 - импульс силы - импульс силы  за малый промежуток времени t. Вектор импульса силы сонаправлен с вектором силы. за малый промежуток времени t. Вектор импульса силы сонаправлен с вектором силы.
| 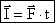 [ I ]= Н.с
[ I ]= Н.с
|
| Импульс тела. (Количество движения) Векторная физическая величина, являющаяся мерой механического движения и равная произведению массы тела на его скорость. Вектор импульса тела сонаправлен с вектором скорости тела. | 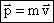 [ p ]= кг м/с
[ p ]= кг м/с
|
| Основное уравнение динамики | |
Из второго закона Ньютона: 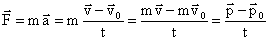
| |
Тогда получим: 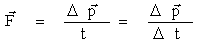 - второй закон Ньютона в импульсной форме - второй закон Ньютона в импульсной форме
| 
|
| (Dt = t - t0 = t при t0 = 0). | |
| Импульс силы равен изменению импульса тела. Вектора импульса силы и изменения импульса тела сонаправлены. | 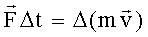
|
Неупругий удар (шарик "прилипает" к стенке):

| 
|
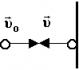
Абсолютно упругий удар (шарик отскакивает с прежней по величине скоростью):
| 
|
| Закон сохранения импульса. | |
До взаимодействия
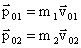
| 
|
После взаимодействия

| 
|

| |
Согласно 3 з-ну Ньютона: 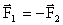 , следовательно: , следовательно: 
| 
|
| Геометрическая (векторная) сумма импульсов взаимодействующих тел, составляющих замкнутую систему, остается неизменной. | |
| Замкнутой называется система тел, взаимодействующих только друг с другом и не взаимодействующих с другими телами. Можно пользоваться и для незамкнутых систем, если сумма внешних сил, действующих на тела системы, равна нулю, или процесс происходит очень быстро, когда внешними воздействиями можно пренебречь (взрыв, атомные процессы). | |
В общем виде: т.к. система замкнутая, то 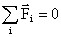 , следовательно , следовательно 
| 
|
Примеры применения закона сохранения импульса:
| |
Реактивное движение.
| Реактивное движение. | |
| Под реактивным понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела. При этом возникает т.н. реактивная сила, сообщающая телу ускорение. | |
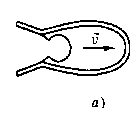
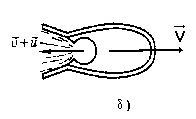
Уравнение Циолковского: Пусть в некоторый момент времени скорость ракеты относительно инерциальной системы, связанной со звездами, равна  (рис. а), а масса ракеты равна М. Скорость истечения газов относительно выбранной инерциальной системы отсчета равна (рис. а), а масса ракеты равна М. Скорость истечения газов относительно выбранной инерциальной системы отсчета равна  , т.к. до начала сгорания топливо имело ту же скорость, что и ракета, а масса топлива m.
Через малый интервал времени D t масса ракеты станет равной , т.к. до начала сгорания топливо имело ту же скорость, что и ракета, а масса топлива m.
Через малый интервал времени D t масса ракеты станет равной  , где m - расход топлива (Расходом топлива называется отношение массы сгоревшего топлива ко времени его сгорания). За этот же промежуток времени скорость ракеты изменится на , где m - расход топлива (Расходом топлива называется отношение массы сгоревшего топлива ко времени его сгорания). За этот же промежуток времени скорость ракеты изменится на 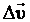 и станет равной и станет равной  . Тогда получим: . Тогда получим:  Раскрыв скобки:
Раскрыв скобки: 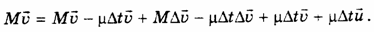 Слагаемым
Слагаемым 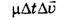 можно пренебречь по сравнению с остальными. После приведения подобных членов будем иметь: можно пренебречь по сравнению с остальными. После приведения подобных членов будем иметь: 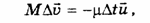 или или 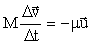 - уравнение Мещерского для движения тела переменной массы (1897 г.). Обозначим - уравнение Мещерского для движения тела переменной массы (1897 г.). Обозначим  . Если учесть действие не только реактивной, но и внешней силы, то закон движения для реактивного движения будет выглядеть следующим образом: . Если учесть действие не только реактивной, но и внешней силы, то закон движения для реактивного движения будет выглядеть следующим образом: 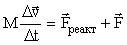 .
Если представить, что все топливо вытекает одновременно, то согласно закону сохранения импульса: Mv- mu = 0 или .
Если представить, что все топливо вытекает одновременно, то согласно закону сохранения импульса: Mv- mu = 0 или 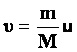 .
Здесь m - масса топлива.
Следовательно, скорость движения ракеты тем больше, чем больше скорость истечения топлива и чем большую часть составляет масса топлива от массы ракеты. Поскольку .
Здесь m - масса топлива.
Следовательно, скорость движения ракеты тем больше, чем больше скорость истечения топлива и чем большую часть составляет масса топлива от массы ракеты. Поскольку 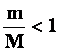 , то v < u. , то v < u.
| 
|
 2020-08-05
2020-08-05 110
110








