Криптография с открытым ключом

В основе теоретико-сложностный подход.

Односторонние функции F:X→Y

а) существует полиномиальный алгоритм вычисления

y=F(x);

б) не существует полиномиального алгоритма инвертирования функции F, т.е. решения уравнения

F(x)=y относительно x.

Более сильное требование, чем принадлежность к NP-полным проблемам, т.к. требуется отсутствие полиномиального алгоритма почти всюду.

Функция с секретом f_K: X→ Y

а) при любом к существует полиномиальный алгоритм вычисления f_K;

б) при неизвестном к не существует полиномиального алгоритма инвертирования данной функции;

в) при известном к существует полиномиальный алгоритм ее инвертирования.

Дифи У., Хеллман М. Защищенность и имитостойкость. Введение в криптографию // ТИИЭР т.67, №3, 1979

RSA

Алгоритм шифрования, в основе сложная задача факторизации больших чисел

1. Абонент выбирает пару простых чисел: p и q вычисляет и публикует n=pq

2.Функция Эйлера: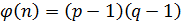

3. Случайное e

4. Вычисляем d: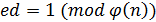

5. Открытый ключ; (n,e)

6. Секретный ключ: ()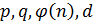

Шифрование: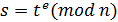

Расшифрование: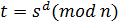

 

Задача. Зашифровать аббревиатуру RSA при p=17, q=31.

Решение

1) Вычисляем модуль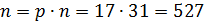

2) Функция Эйлера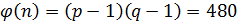

3) Случайное е, т.ч. 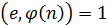, например е = 7.

4) Вычисляем d, т.ч. e d=1(mod 480), d=343, т.к.

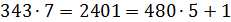
5) Переведем слово «RSA» в числовой вид:

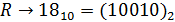
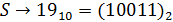
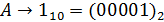
Общая последовательность (с учетом диапазона [0,526]):

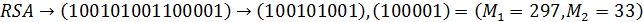
6) Шифруем последовательно M₁ и M₂

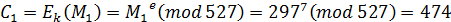
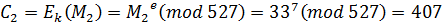
Получаем шифрограмму: С= (474,407)

7) Расшифрование

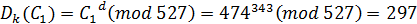
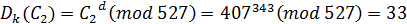
Для упрощения вычислений можно использовать соотношение:

343=256+64+16+4+2+1

Домашнее задание: написать программу на языке, реализующую RSA, проверить Пример для теста - зашифровать и расшифровать последовательность, включающую свои имя и фамилию (без пробела) + 3 собственных примера.