Использование Z – преобразования

 

Для последовательностей f(u) может быть введено понятие дискретного преобразования Лапласа, определяемое формулой

                                                                                          (*)

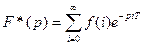Для смещенных последовательностей может быть записано аналогичное выражение:

.                                                                             (**)

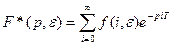Эти формулы можно представить в символической записи:

.

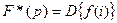
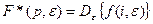В приведенных формулах, как и в случае непрерывного преобразования Лапласа, комплексная величина p = α + iω, где α – абсцисса абсолютной сходимости.

Как следует из (*) и (**), изображение является функцией величины e^pT.

Для исследования импульсных систем большое распространение получило так называемое z-преобразование, которое связано с дискретным преобразованием Лапласа и вытекает из него. Применительно к z-преобразованию ниже будут рассмотрены основные свойства и теоремы дискретного преобразования Лапласа.

Под z-преобразованием понимается изображение несмещенной или смещенной последовательностей, определяемое формулами

,         ,                                     (***)

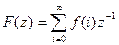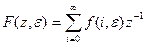В этих формулах введено новое обозначение z = e^pT. Из них следует, что z-преобразование практически совпадает с дискретным преобразованием Лапласа и отличается только аргументом изображения.

Формулы преобразования (***) могут быть записаны в символической форме:

F(z) = Z{f(i)}, F(z,ε) = Z_ε{f(i,ε)}.

Формулы преобразования могут быть записаны и для непрерывной производящей функции в виде:

F(z) = Z{f(t)},     t = iT,

F(z, ε) = Z _ε{f(t)}, t = (i + ε)T,

где i = 0,1,2,...

Рассмотрим кратко основные правила и теоремы применительно к z-преобразованию. Эти же правила и теоремы будут справедливыми и для дискретного преобразования Лапласа. Эти теоремы приведены для несмещенных последовательностей, но полученные результаты можно распространить и на случай смещенных последовательностей, кроме случаев, оговоренных особо.

1. Свойство линейности.

Это свойство заключается в том, что изображение линейной комбинации последовательностей равно той же линейной комбинации их изображений. Пусть

.

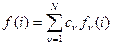Тогда можно записать

.

 

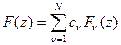2. Теорема запаздывания и упреждения.

Рассмотрим последовательность f(i – m), сдвинутую вправо (запаздывающую) на целое число тактов m. Тогда из формулы (***) следует, если обозначить i – m = r,

.

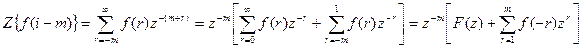Здесь F(z) – изображение f(i). Если исходная последовательность f(i) равна нулю при отрицательных значениях аргумента, то формула упрощается:

Z{f(i – m)} = z^-mF(z).

Если сдвиг происходит влево (упреждение) и рассматривается последовательность     f(i + m), где m – целое положительное число, то аналогично случаю запаздывания можно показать, что

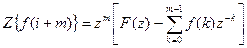
Второе слагаемое в правой части этого уравнения обращается в нуль, если f(i) = 0при i = 0,1,.....,m-1.

При запаздывании на не целое число периодов m + ξ приходится вводить смещенную последовательность f(i + ε – m – ξ), где m – целая, а ξ – дробная часть запаздывания. Если смещение ε удовлетворяет условию 0≤ ε < ξ и f(i + ε –m –ξ) тождественно равно 0 при i + ε < m – ξ, то можно показать, что

Z _ε{f(i + ε – m – ξ)} = z^-(1+m)F(z,1 + ε – ξ).

Если ξ≤ ε <1, то

Z _ε{f(i + ε – m – ξ)} = z^-mF(z,ε – ξ).

При использовании таблицы для нахождения изображений следует вместо ε подставить 1 + ε – ξ или ε – ξ в соответствии последними формулами.

3. Сумма ординат последовательности.

Если абсцисса абсолютной сходимости отрицательна α<0, то подставив (***) р = 0, имеем:

.

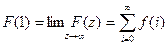4. Конечное значение последовательности

Составим первую прямую разность последовательности f(i) и на основании свойства линейности найдем ее изображение

Z{∆f(i)} = (z-1)F(z) – zf(0).

Далее на основании свойства (3) найдем сумму ординат ∆f(i):

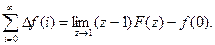
Кроме того, можно записать

.

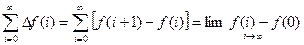Из двух последних выражений следует:

.

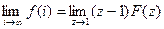5. Формулы разложения.

Если изображение представляет собой простейшую табличную форму, то переход к оригиналу не представляет трудностей. Сложная дробно-рациональная форма может быть представлена в виде суммы дробей первой степени.

6. Разложение в ряд Лорана.

Из основного выражения z-преобразования (***) следует:

.

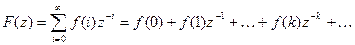Разложим любым способом изображение F(z) в ряд Лорана (ряд по убывающим степеням z):

F(z) = c₀ + c₁z^-1 +... + c_kz^-k +...,

и сравнивая два ряда между собой, можно установить, что с₀ = f(0), c₁ = f(1), c₂ = f(2),..., c_k = f(k) и т.д.

Разложение в ряд можно делать любым способом, т.к. такое разложение единственно. Наиболее удобным приемом для дробно-рациональных функций является деление числителя на знаменатель.

применяя разложение в ряд Лорана, можно вычислить значения оригинала f(i) или f(i, ε) в дискретных точках без нахождения полюсов изображений F(z).

7. Решение разностных уравнений.

Пусть имеется разностное уравнение в форме

,

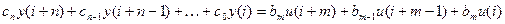с начальными условиями y(ν) = y_ν(ν = 0,1,...,n-1). Найдем z-преобразование для его левой и правой частей. В соответствии с формулой теоремы запаздывания и упреждения для случая упреждения на n тактов:

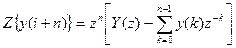
 Аналогичные зависимости могут быть записаны для упреждения на (n-1), (n-2),...,1 тактов.

Для входной последовательности начальные условия не задаются. Поэтому

Z{u(i+m)} = z^mU(z).

В результате при переходе в рассматриваемом разностном уравнении к изображениям получим:

C(z)Y(z) – Y₀(z) = B(z)U(z),

где C(z) = c₀zⁿ + c₁z^n-1 +... + c_n, B(z) = b₀z^m + b₁z^m-1 +...+ b_m, аY₀(z) – сумма членов, определяемых начальными условиями.

Из последнего выражения можно найти изображение искомой выходной последовательности

.                                                                (+)

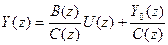Далее можно использовать изложенные выше приемы перехода к искомому оригиналу y(i).

Для решения рассматриваемого разностного уравнения необходимо, как следует из изложенного, знать начальные условия y(ν) = y_ν(ν = 0,1,...,m-1). Последние же зависят от вида действующей в правой части разностного уравнения входной последовательности.

Более удобны для решения разностные уравнения вида

, (**)

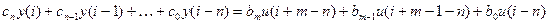с начальными условиями  y(ν) = y_ν(ν = 0,1,...,n-1).

Изображение последовательности y(i-n), запаздывающей на n тактов, в соответствии со 2-м свойством будет:

.

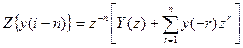Подобные зависимости могут быть записаны для запаздывания на (n-1), (n-2),..., 1 тактов.

y(ν) = y_ν(ν = 0,1,...,n-1).

Особый интерес представляет случай, когда до момента времени t = 0 искомая последовательность тождественно равна 0. Это эквивалентно случаю нулевых начальных условий слева (при t = -0) при решении дифференциальных уравнений для непрерывных функций. Тогда в выражении (+) для изображения пропадает член в правой части, определяемый начальными условиями, и оно приобретает вид

                                                                              (++)

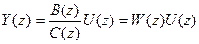Здесь введена дискретная передаточная функция W(z), которая, как и в случае непрерывных функций, есть отношение двух изображений (выходной и входной величин) при нулевых начальных условиях. Дискретная передаточная функция играет такую же роль в импульсных и цифровых системах, как и обычная передаточная функция в непрерывных системах.