Разностные уравнения

ОБЩИЕ ВОПРОСЫ ЦИФРОВОГО УПРАВЛЕНИЯ.

 

        Сигналы, действующие в системах автоматического управления, бывают непрерывными и дискретными. Соответственно этому САУ делятся на системы непрерывного и дискретного действия.
          В свою очередь дискретные САУ делятся на релейные, импульсные и цифровые. Релейные САУ - это системы с квантованием по уровню, импульсные - с квантованием по времени, а цифровые - с применением обоих видов квантования.

 

Импульсные системы.

 

Линейной импульсной системой называется такая система автоматического управления, которая кроме звеньев, описываемых линейными дифференциальными уравнениями, содержит импульсный элемент, преобразующий непрерывное входное воздействие в последовательность импульсов (рис. 5.1).

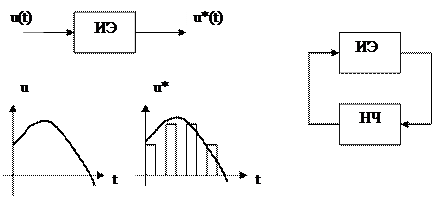
а)                                                                   б)  

Рис. 5.1. Структурная схема импульсного элемента (а) и импульсной системы (б).

 

В общем случае можно изобразить обобщенную структурную схему импульсной системы так, как показано на рис. 5.1 б, где все непрерывные звенья сведены в один блок – непрерывную часть системы НЧ. Последняя может иметь какую угодно структуру (любой сложности, с обратными связями и т.п.).

Импульсный элемент может представлять собой самостоятельное функциональное устройство или являться составной частью цифро-аналоговых преобразователей, входящих в систему управления с цифровыми управляющими машинами (ЦВМ).

В процессе преобразования непрерывного сигнала в дискретный импульсный элемент выполняет две операции: квантование по времени и импульсную модуляцию. Первая из них состоит в том, что сигнал u*(t) появляется в дискретные моменты времени t = t_i(i = 0,1,2,...). Чаще всего эти моменты времени равноотстоящие, т.е. t_i = iT, где Т – период дискретности. В результате импульсной модуляции изменяется какой-либо параметр импульса (амплитуда, ширина). Форма импульсов может быть любой (прямоугольной, трапецеидальной и т.д.), но обычно используются импульсы прямоугольной формы.

Наиболее распространенными в настоящее время видами импульсной модуляции являются амплитудно-импульсная (АИМ) и широтно-импульсная (ШИМ).

При амплитудно-импульсной модуляции модулируемым параметром служит амплитуда (высота) импульсов. Обычно она пропорциональна значениям непрерывного сигнала u(t) в дискретные моменты времени t = iT(i = 0,1,2,...), т.е. значениям

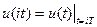
Сигнал u*(t) на выходе импульсного элемента (рис. 5.2) формируется в виде

,

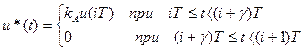где k_А – коэффициент пропорциональности, γ – скважность импульсов (0<γ<1), которая остается постоянной.

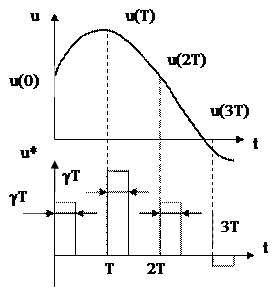
Рис. 5.2 Амплитудно-импульсная модуляция.

 

При широтно-импульсной модуляции модулируемым параметром является ширина или длительность импульсов τ_i = γ_iT, где γ_i = γ(iT) – скважность i-го импульса. Амплитуда импульсов при этом остается постоянной. Сигнал на выходе импульсного элемента (широтно-импульсного модулятора) формируется в виде

,

 

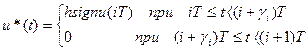где h – амплитуда импульсов, а sign u(iT) означает знак величины u(iT).

В зависимости от способа определения текущего значения скважности γ_i различают широтно-импульсную модуляцию 1-го рода (ШИМ-1) и 2-го рода (ШИМ-2).

При ШИМ-1 (Рис. 5.3.а) скважность i-го импульса

,

 

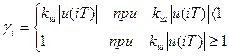где k_ш – коэффициент пропорциональности (крутизна характеристики широтно-импульсного модулятора).

Так как длительность импульса τ_i = γ_iT не может быть больше периода дискретности Т, то при │u(iT)│≥k_ш^-1 скважность γ_i = 1, т.е. происходит насыщение модулятора.

При ШИМ-2 (рис. 5.3. б) длительность импульсов определяется в результате сравнения непрерывного входного сигнала u(t) с некоторым периодическим опорным сигналом u_оп(t), в качестве которого обычно используется пилообразный сигнал, формируемый специальным генератором. Импульсы запускаются в моменты времени t = iT и существуют до момента совпадения сигналов u(t) и u_оп(t). Как правило, ШИМ-2 используется в системах, в которых сигнал u(t) не меняет свой знак. Примером может служить система стабилизации напряжения.

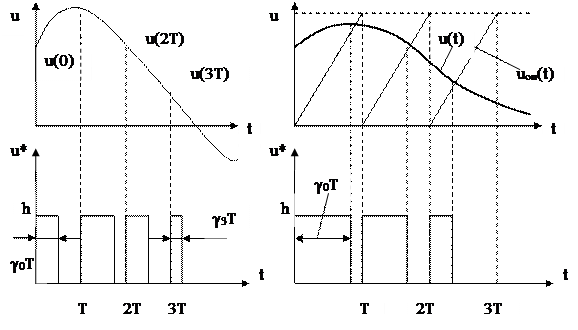
а)                                                                  б)

Рис. 5.3. Широтно-импульсная модуляция.

 

Разностные уравнения.

 

В импульсной системе на вход непрерывной части поступает последовательность импульсов u*(t), модулированных по амплитуде. Несмотря на то, что непрерывная часть описывается линейным дифференциальным уравнением и сам импульсный элемент является линейным, получить дифференциальное уравнение системы, как это делалось ранее, не представляется возможным из-за разрывного характера сигнала u*(t). Поэтому для исследования импульсных систем вместо дифференциальных уравнений используют так называемые разностные уравнения.

 

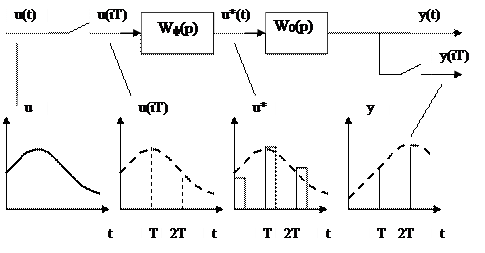
Рис. 5.4. Пример разомкнутой импульсной системы.

 

Рассмотрим разомкнутую систему, состоящую из импульсного элемента и непрерывной части. Ее схему представим, как показано на рис. 5.4., где W₀(p) – передаточная функция непрерывной части, а импульсный элемент условно заменен последовательным соединением ключа и некоторого формирующего устройства с передаточной функцией W_ф(p). Ключ периодически с периодом Т замыкается на очень короткий промежуток времени и выделяет из непрерывного сигнала u(t) его мгновенные значения u(iT). Формирующее устройство образует из этих значений импульсы прямоугольной формы так, как показано на рис. 5.4. В этой схеме W0(p) – передаточная функция непрерывной части, а импульсный элемент условно заменен последовательным соединением ключа и некоторого формирующего устройства с передаточной функцией Wф(p).

Ключ периодически с периодом Т замыкается на очень короткий промежуток времени и выделяет из непрерывного сигнала u(t) его мгновенные значения u(iT). Формирующее устройство образует из этих значений импульсы прямоугольной формы так, как показано на рис. 5.2.

Будем полагать, что входным сигналом системы является не u(t), а u(iT), или в сокращенной записи u(i). Несмотря на то, что сигнал y(t) в общем случае непрерывен, в качестве выходного сигнала системы будем рассматривать y(iT), или в сокращенной записи y(i). Условно это отображено на рис. 5.4 наличием ключа на выходе непрерывной части.

Последовательности типа u(i) и y(i) иногда называют решетчатыми функциями, хотя в строгом понимании они функциями не являются.

Аналогом первой производной непрерывной функции для любой последовательности f(i) служит конечная разность 1 – го порядка или первая разность

∆f(i) = f(i+1) – f(i).

Она определяется в момент времени t = iT как разность между будущим значением последовательности при t = (i+1)T и текущим значением при t = iT.

Аналогом второй производной непрерывной функции для последовательности является конечная разность 2 – го порядка или вторая разность

∆²f(i) = ∆[∆f(i)] = ∆f(i+1) - ∆f(i) = f(i+2) – 2f(i+1) + f(i).

В общем случае для k – ой разности можно записать

,

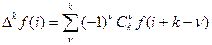где

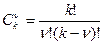
- биноминальные коэффициенты.

В качестве аналога дифференциального уравнения можно рассматривать уравнение в конечных разностях. Применительно к системе, изображенной на рис. 11.4. оно имеет вид

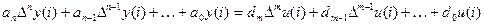
где m ≤ n.

Однако при исследовании дискретных систем удобнее пользоваться уравнением

, (*)

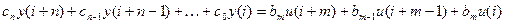которое получается из предыдущего. Оно и называется разностным уравнением.

Это уравнение можно представить и в ином виде:

, (**)

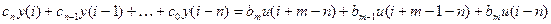Разностные уравнения по существу являются рекуррентными соотношениями, позволяющими при i = 0,1,2,... последовательно шаг за шагом (т.е. рекуррентно) вычислять значения выходной величины y(i) при заданных ее начальных значениях и любых заданных аналитически, графически или таблично значениях входной величины u(i). Например, из уравнения (**), задав начальные значения y(-n), y(-n+1),...,y(-1) и значения u(i) можно последовательно найти y(0), y(1), y(2),...,y(n).  Такие вычисления легко машинизируются, а также не представляют никаких принципиальных трудностей и при ручном счете (кроме, конечно, затрат времени) даже в случае, когда коэффициенты разностного уравнения с течением времени изменяются. Это отличает разностные уравнения от их непрерывных аналогов – дифференциальных уравнений.

Общее решение неоднородного разностного уравнения, как и решение неоднородного дифференциального уравнения, представляется в виде суммы переходной и вынужденной составляющих. Переходная составляющая, т.е. общее решение однородного уравнения, определяется следующим образом:

y(i) = C₁z₁ⁱ + C₂z₂ⁱ +... + C_nz_nⁱ,                                                    (***)

где z_ν(ν = 1,2,...,n) – некратные корни характеристического уравнения

c₀zⁿ + c₁z^n-1 +... c_n = 0,

которое легко получается из (*), а С_ν – произвольные постоянные.

Из (***), в частности, вытекает условие затухания свободного движения системы, описываемой разностным уравнением (*), т.е. условие устойчивости:

│z_ν│< 1                       (ν = 1,2,...,n).

Решение разностного уравнения y(i) дает значения выходной величины лишь в дискретные моменты времени t = iT. Во многих случаях этого вполне достаточно для суждения о поведении системы. Если же возникает необходимость в получении информации об изменении выходной величины в любой момент времени, то используется смещенная последовательность (рис. 5.5):

y(iT + εT) = y(t)│_t=iT+εT,

или в сокращенной записи y(i,ε), где ε – параметр, которому можно придавать любые значения в пределах 0≤ε≤1. Если ε изменять непрерывно в указанных пределах, то    y(i, ε) совпадет с y(t).

 

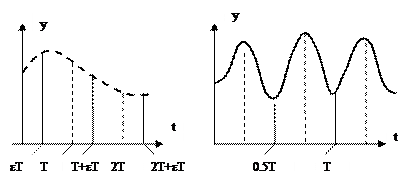
Рис. 5.4 Пример смещенной последовательности.

 

Смещенная последовательность y(i,ε) представляет собой решение разностного уравнения со смещенным аргументом

c₀y(i+n, ε) + c₁y(i+n-1, ε)+...+c_ny(i+ε) = b₀(ε)u(i+m) + b₁(ε)u(i+m-1)+...+b_mu(i),

которое при ε = 0 превращается в уравнение (*).

Значения выходной величины y(i, ε) можно вычислить последовательно шаг за шагом при заданных начальных значениях и значениях входной величины u(i).

Переходная составляющая, т.е. общее решение однородного уравнения, определяется в этом случае следующим образом:

y(i, ε) = C₁z₁^i+ε + C₂z₂^i+ε +...+ C_nz_n^i+ε,

где z_ν (ν = 1,2,...,n) – некратные корни характеристического уравнения.

В качестве примера исследуем процессы в системе, разностное уравнение со смещенным аргументом которой имеет вид

y(i+2, ε) - 0.27y(i+1, ε) + 0.135y(i, ε) = (1-e^-2εcos4πε)u(i+2) – (0.135-e^-2εcos4πε)u(i+1) (*)

при начальных значениях y(-1, ε) = y(-2, ε) = 0 и единичной входной последовательности u(0) = u(1) =... = 1.

положив ε = 0, получим обыкновенное разностное уравнение:

y(i+2) – 0.27y(i+1) = 0.135y(i) = 0.865u(i+1).                                                        (**)

Корни характеристического уравнения

z² – 0.27z + 0.135 = 0;

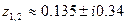
удовлетворяют условию устойчивости.

Из уравнения (**) при y(-1) = y(-2) = 0 последовательно шаг за шагом находим значения выходной величины в моменты времени t = iT:

y(0) = 0.27y(-1) – 0.135y(-2) + 0.865u(-1) = 0

y(1) = 0.27y(0) – 0.135y(-1) + 0.865u(0) = 0.8654;

y(2) = 0.27y(1) – 0.135y(0) + 0.865u(1) = 1.098;

y(3) = 0.27y(2) – 0.135y(1) + 0.865u(2) = 1.045;

Продолжая вычисления, убеждаемся, что в дискретные моменты времени t = iT процесс монотонный, а выходная величина стремится к установившемуся значению y_уст = 1.

Аналогично решая уравнение (*) получим:

y(0,ε) = 1-e^{-2 ε}cos4π ε;

y(1,ε) = 1.135 – 0.27e^{-2 ε}cos4π ε;

y(2,ε) = 1.036 + 0.062e^{-2 ε}cos4π ε;

Кривая y(t) изображена на рис. 5.4. б, где отмечены ее значения при ε = 0; 0.25; 0.5; 0.75.