Устойчивость импульсных систем

Ранее было показано, что непрерывная система устойчива, если все корни ее характеристического уравнения лежат в левой полуплоскости. При исследовании импульсных систем вместо р используется новая переменная z = e^pT. В теории функций комплексного переменного преобразования, в процессе которого одна переменная заменяется некоторой функцией от новой переменной, а одна область комплексной плоскости отображается в другую, называется конформным преобразованием. конформное преобразование z = e^pT отображает левую полуплоскость плоскости р в область, ограниченную окружностью единичного радиуса на плоскости z (рис. 5.6). При этом мнимая ось плоскости р отображается в саму окружность.

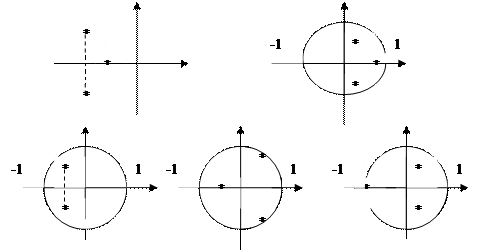
Рис. 5.6. Иллюстрации к вопросу устойчивости импульсных систем.

Действительно, пусть 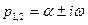. Тогда

При этом 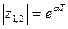. Для значений α ‹ 0 (что соответствует корням р_1,2 в левой полуплоскости) 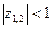, что соответствует корням, лежащим внутри круга единичного радиуса плоскости z. Если α = 0, т.е. если корни р_1,2 располагаются на мнимой оси плоскости р, то корни z_1,2 попадают на окружность единичного радиуса плоскости z.

Таким образом, импульсная система устойчива, если все корни ее характеристического уравнения лежат внутри круга единичного радиуса, т.е. если 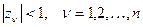. Если хотя бы один корень лежит вне круга единичного радиуса, то система неустойчива.

Окружность единичного радиуса представляет собой границу устойчивости для импульсной системы.

Система находится на апериодической границе устойчивости, если в ее характеристическом уравнении

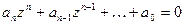
имеется корень z_ν = 1. а остальные корни располагаются внутри единичного круга. В этом случае переходная составляющая решения разностного уравнения с течением времени стремится к значению .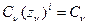

Если в характеристическом уравнении имеется пара комплексно сопряженных корней, расположенных на окружности единичного радиуса, то имеет место колебательная граница устойчивости. В этом случае с течением времени в системе устанавливаются незатухающие периодические колебания.

Типичной для импульсных систем является так называемая граница устойчивости третьего типа, которой соответствует наличие в характеристическом уравнении корня z_ν = -1. В этом случае в системе с течением времени устанавливаются незатухающие периодические колебания с периодом, равным 2Т.

Обычно для оценки устойчивости и качества импульсных систем используется передаточная функция разомкнутой системы W(z) и передаточная функция замкнутой системы Ф(z). Тогда характеристическое уравнение замкнутой системы может быть получено следующим образом:

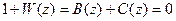где B(z), C(z) – полиномы числителя и знаменателя передаточной функции W(z).

Исследование устойчивости импульсных систем представляет собой более сложную задачу, чем исследование устойчивости непрерывных систем. Это связано с тем, что рассмотренные ранее критерии устойчивости, такие как критерий Гурвица, устанавливают принадлежность корней характеристического уравнения в левой полуплоскости, тогда как для устойчивости импульсной системы корни характеристического уравнения должны находиться внутри круга единичного радиуса на плоскости z. По той же причине неприменимым оказывается и необходимое условие устойчивости, требующее положительности коэффициентов характеристического уравнения. Например, в уравнении z – 0.5 = 0 один коэффициент отрицательный, однако корень z₁ = 0.5 находится внутри круга единичного радиуса.

Принадлежность корней кругу единичного радиуса может быть установлена при помощи критерия Шур-Кона. До некоторой степени он аналогичен критерию Гурвица, однако при его использовании необходимо составлять и анализировать определители вплоть до определителя порядка 2n*2n, где n – порядок характеристического уравнения. Поэтому на практике этот критерий применяется редко.

Для того, чтобы получить возможность использования для исследования устойчивости импульсных систем всех критериев устойчивости непрерывных систем, необходимо отобразить круг единичного радиуса с плоскости z на левую полуплоскость некоторой новой переменной. В теории функций комплексного переменного существует преобразование

, (*)

которое называется билинейным, или ω-преобразованием. Оно также отображает круг единичного радиуса на левую полуплоскость, но уже не плоскости р, а плоскости переменной ω.

Рассмотрим, например характеристическое уравнение 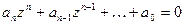при n = 1. После подстановки (*) получим:

Для уравнений первого и второго порядка, необходимое и достаточное условие устойчивости сводится к требованию положительности коэффициентов. Таким образом, условия устойчивости импульсной системы при n = 1 имеют вид

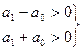
При n = 2 характеристическое уравнение и условия устойчивости следующие:

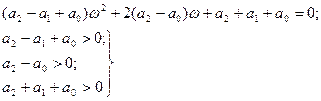
При n = 3 кроме положительности коэффициентов должно дополнительно выполняться условие критерия Гурвица. Поэтому для исследования устойчивости требуется проверить выполнение пяти неравенств:

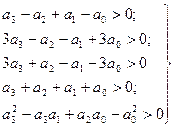
В качестве примера исследуем устойчивость замкнутой системы, передаточная функция непрерывной части которой

При помощи таблицы z-преобразования находим передаточную функцию разомкнутой системы:

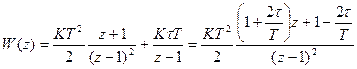Характеристическое уравнение замкнутой системы имеет вид:

Здесь n = 2, поэтому условия устойчивости замкнутой системы:

Для исследования устойчивости замкнутых систем удобно использовать критерий Найквиста. Чтобы построить амплитудно-фазовую характеристику разомкнутой системы можно использовать преобразование z = e^pT. Заменив p = iω, получим:

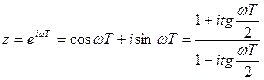подставив эту формулу в выражение для передаточной функции разомкнутой системы W(z), найдем частотную передаточную функцию разомкнутой системы W(e^iωT). Определив модуль и фазу или вещественную и мнимую части этой функции, можно построить АФХ разомкнутой системы.

Следует учитывать, что эта функция периодическая. Поэтому при построении АФХ достаточно ограничиться диапазоном частот от 0 до π/Т.

В качестве примера рассмотрим систему, передаточная функция непрерывной части которой

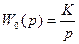Передаточная функция разомкнутой системы:

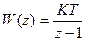В результате замены получим:

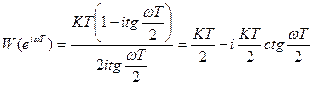АФХ разомкнутой системы изображена на рис. 5.7. Т.к. при ω = 0 она имеет разрыв, обусловленный наличием р в знаменателе W₀(p), дополняем ее четвертью окружности бесконечно большого радиуса.

Для исследования устойчивости замкнутой системы можно использовать любую из приведенных формулировок критерия Найквиста. В знаменателе передаточной функции W₀(p) нет корней с положительной вещественной частью, т.е. l = 0. поэтому АФХ разомкнутой системы не должна охватывать точку (-1, i0).