Передаточные функции

 

В предыдущем параграфе было показано, что передаточная функция W(z) системы, схема которой представлена на рис. 5.4, легко определяется если известно разностное уравнение. В соответсвии с (++) она имеет вид

,                                                                                       (*)

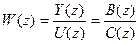где B(z) и C(z) – полиномы, входящие в уравнение.

Однако на самом деле заданным является не разностное, а дифференциальное уравнение непрерывной части системы. Поэтому, наоборот, один из способов получения разностного уравнения основан на использовании уже известной передаточной функции W(z).

Действительно, если известна передаточная функция (*), то сразу определяется уравнение для изображений (+). Из него получаются разностные уравнения.

С учетом отмеченного передаточную функцию W(z) будем определять непосредственно по структурной схеме системы (рис. 5.4).

В качестве входной величины системы целесообразно рассматривать последовательность u(i), изображение которой U(z), а в качестве выходной – последовательность y(i), изображение которой Y(z). Тогда, как видно из рис. 5.4,

Y(z) = Z{W_ф(p)W₀(p)}U(z)

и передаточная функция (*) может быть определена следующим образом:

W(z) = Z{W_ф(p)W₀(p)}.                                                             (**)

Последовательное соединение формирующего устройства с передаточной функцией W_ф(p) и непрерывной части с передаточной функцией W₀(p) иногда называют приведенной непрерывной частью системы. Передаточная функция W(z) должна определяться по ее результирующей передаточной функции W_ф(p)W₀(p). Это связано с тем, что z-преобразования от произведения передаточных функций непрерывных звеньев, не разделенных импульсным элементом (ключом), не равна произведению z-преобразований:

Z{W_ф(p)W₀(p)}≠Z{W_ф(p)}Z{W₀(p)}.

Поэтому иногда для последовательного соединения двух звеньев, передаточная функция записывается в виде W(z) = W_фW₀(z), причем W_фW₀(z)≠W_ф(z)W₀(z).

Передаточная функция W₀(p) полагается заданной. Для нахождения передаточной функции формирующего устройства W_ф(p) положим, что оно генерирует прямоугольные импульсы длительностью γТ. Коэффициент пропорциональности k_А можно отнести к непрерывной части системы. Тогда амплитуда (высота) импульсов будет равна u(i).

Передаточная функция W_ф(p) может быть определена как отношение изображений по Лапласу выходной величины формирующего устройства U*(p) и его входной величины. Однако входная величина представляет собой последовательность u(i), для которой преобразование Лапласа не существует. Чтобы устранить эту неопределенность положим, что идеальный импульсный элемент (ключ) генерирует не импульсы конечной высоты u(i), а бесконечно короткие импульсы типа дельта-функций, площади которых пропорциональны значениям u(i).

На самом деле никакой импульсный элемент не может генерировать бесконечные по высоте импульсы. Вместе с тем возможность использования указанного формального представления при теоретических исследованиях является обоснованной.

При поступлении на вход формирующего устройства единственной дискреты u(i) высотой, равной единице, на его выходе образуется прямоугольный импульс с такой же высотой и длительностью γТ. Его изображение:

.                                                           (***)

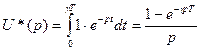Но так как указанная дискрета формально заменяется единичной дельта-функцией, выражение которой по Лапласу равно единице, то изображение (***) представляет собой передаточную функцию формирующего устройства:

.

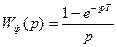В этом случае передаточная функция (**)

.

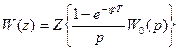Последнее выражение неудобно для практического применения. Поэтому воспользуемся теоремой смещения z-преобразования в вещественной области, согласно которой ,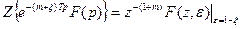

где m =0, 1, 2,…; 0 ≤ ξ ≤ 1. Положив m = 0, ξ = γ, получим:

.                                  (+)

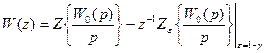Пусть, например, непрерывная часть системы имеет передаточную функцию

.

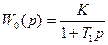Тогда в соответствии с (+) и таблицей z-преобразования получим

,

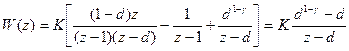где .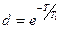

В системах автоматического управления преимущественно используются формирующие устройства, удерживающие на выходе величину, равную u(i), в течение всего периода дискретности Т. В этом случае γ = 1, а само формирующее устройство называется экстраполятором нулевого порядка. Передаточные функции при γ = 1 принимают вид

.

.                                                                (++)

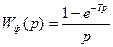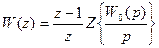Определим, например, передаточную функцию для случая, кгода непрерывная часть имеет вид:

.

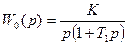Чтобы можно было использовать данные таблицы z-преобразования, разложим правую часть на простые дроби:

.

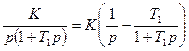Тогда получим:

 

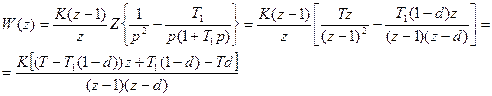
В непрерывную часть системы может входить звено с чистым временным запаздыванием τ, что соответствует наличию в передаточной функции W_o(p) сомножителя 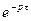. Если величина τ находится в пределах от 0 до Т, то передаточную функцию с учетом m = 0 и ξ = τ, можно записать следующим образом:

.

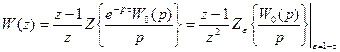В ряде случаев для получения более полной информации об изменении выходной величины системы применяется так называемая модифицированная передаточная функция

,

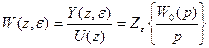где .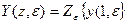

Однако большинство задач по исследованию дискретных систем решается при использовании передаточной функции W(z).

Рассмотрим теперь замкнутую импульсную систему.

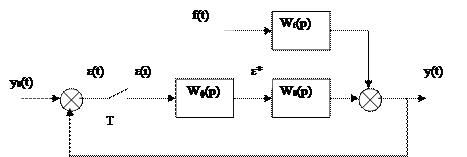
Рис. 5.5. Замкнутая импульсная система.

 

Ее структурная схема может быть представлена так, как показано на рис. 5.5., где W_f(p) – передаточная функция разомкнутой системы по возмущению. Основу этой системы составляет схема, изображенная на рис 5.4, при x(i) = u(i). Тогда изображение управляемой величины y(t) при f(t) = 0

,                                                                         (*)

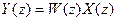где W(z) – передаточная функция разомкнутой системы, которая при использовании экстраполятора нулевого порядка имеет вид (++).

Так как приведенная непрерывная часть системы реагирует на значения ошибки системы ε(t) только в дискретные моменты времени t = iT, то ε(i) = y₀(i) – y(i), а ε(z) = y₀(z) – y(z), и из (*) получим:

,

,

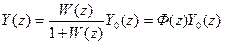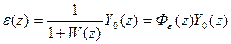где Ф(z) – передаточная функция замкнутой системы, а Ф_ε(z) – передаточная функция замкнутой системы по ошибке (по своей структуре эти передаточные функции аналогичны передаточным функциям замкнутой непрерывной системы).

Передаточная функция импульсной системы (рис. 5.5) по возмущению Ф_f(z) не существует. Это связано с тем, что если F(p) представляет собой изображение по Лапласу функции f(t), то

.

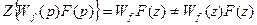При наличии возмущения для разомкнутой системы получим:

.

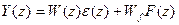Отсюда с учетом выражения ε(z) = y₀(z) – y(z) для замкнутой системы имеем:

.

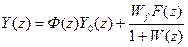Изображение W_fF(z) можно определить только для конкретных заданных воздействий f(t). Однако, это не является препятствием для оценки качества импульсных систем при детерминированных воздействиях.