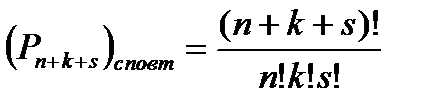Тема занятия: Элементы комбинаторики. Комбинаторные задачи

Дисциплина: ОДП.02 Математика

Группа: ТПОП -19

Дата: 10.06. 2020

Преподаватель: Кулага Т.Ф.

Задание: Ф ото выполненной работы прислать по адресу: kitdistergo@mail.ua kitdisttpop@mail.ua. или https://vk.com/id596417775 личным сообщением

(Название файла с ответами: № занятия, дисциплина, группа, Фамилия, имя, студента).

Например: Иванов И.И., ТПОП -19, Математика

 Сроки выполнения: 11.06.2020

Задания для дистанционного обучения будут выдаваться в день проведения занятия, согласно расписанию и подмен по адресу: https://s3320.nubex.ru/5989/ или VK https://vk.com/ ТПОП-19, https://vk.com/ ТПОП-19

Мотивация  

 «Хотя, как гласит теория вероятности, в принципе может произойти все что угодно, кроме того, что не может произойти никогда.»

Гнеденко Б.В.

Тема занятия: Перестановки. Размещения. Сочетания. Правило суммы и произведения.

Цели:

Цель: ознакомить с понятиями комбинаторики, комбинаций без повторений, комбинаторных принципов сложения и произведения, комбинаций с повторениями: определения, формулы.

Посмотреть и прослушать видеоурок на сайтах Школа InternetUrok.ru, на Youtube по ссылке:

1. https://www.youtube.com/watch?v=Ch7lse6Wf8U

2. https://www.youtube.com/watch?v=Ne6K5wblOvw

Прочитать этот же материал по учебнику А. Алимов и др «Алгебра и начала математического анализа» 10-11 класс, 2016 г гл 11 §62- 64

https://vpr-klass.com/uchebniki/matematika/10-11_klass_alimov/10-11_klass_alimov_uchebnik_chitat'_onlajn.html

Тема занятия: Элементы комбинаторики. Комбинаторные задачи

План: 1. Правило суммы. 2. Правило произведения. 3. Перестановки без повторений. 4. Перестановки c повторениями. 5. Размещения без повторений 6. Сочетания без повторений 7. Треугольник Паскаля. Бином Ньютона 8. Решение задач Элементы комбинаторики Комбинаторика(комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них. Способы решения комбинаторных задач: ü правило суммы; ü правило произведения; ü формулы подсчета количества перестановок, размещений, сочетаний 1. Правило суммы Правило комбинаторной суммы:если элемент a можно выбрать n способами, а элемент b – m способами, причем ни один из способов выбора элемента а не совпадает со способом b, то выбор либо а, либо b можно осуществить n+m способами.  Задача 1. Из города М в город Р ведут две дороги, а в город С – три дороги. Сколькими способами можно проехать из города М либо в город Р, либо в С? Решение: Так как выбор дороги из М в Р можно осуществить двумя способами, а выбор дороги из М в С тремя способами, то согласно правилу суммы количество возможных вариантов 2 + 3=5, т.е. проехать из М в Р или в С можно пятью способами. 2. Правило произведения Правило комбинаторного произведения: пусть имеется n элементов и требуется выбрать один за другим некоторые k элементов. Если первый элемент можно выбрать n1 способами, второй элемент n2 способами, …, и т.д., то число способов, которым могут быть выбраны все k элементов, равно произведению n1∙ n2 ∙…∙ n k. Задача 2. Сколько трехзначных четных шифров можно составить для кодового замка из цифр 0, 1, 2, 3, 4, 5, 6, если цифры в записи шифра могут повторяться? Решение: n1=6 (т.к. в качестве цифры сотен можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве цифры десятков можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве цифры единиц можно взять любую цифру из 0, 2, 4, 6). Итак, N=n1*n2*n3=6*7*4=168. 3 Перестановки без повторений  Комбинации из n элементов, отличающиеся друг от друга только порядком расположения в них элементов, называются перестановками из n элементов.  Число всевозможных перестановок из n элементов обозначают Рn (Р- первая буква французского слова permutation – перестановка). Читается: «Число перестановок из эн элементов». Рn= n!, где 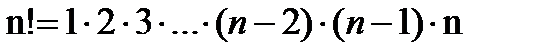. (факториал)   Задача 5. Сколькими способами можно расставить на полке 8 книг, если среди них 2 книги одного автора, которые при любых перестановках должны стоять рядом? Решение: 2 книги одного автора заменим одной книгой, тогда число перестановок из 7 элементов Pn= 7!=5040, но в каждой этой перестановке книги одного автора будут меняться местами то 5040*2=10080 способов. 4. Перестановки c повторениями Пусть имеется n + k + s предметов. Сколькими способами можно разделить эти предметы на три группы так, чтобы в одной группе было n предметов, в другой k предметов, в третьей s предметов? Это задача на перестановки с повторениями. Число перестановок с повторениями находится по формуле:      Задача 3. Сколько анаграмм можно составить из букв слова ИНИЦИАТИВА? И — 4; н — 1; ц — 1; а — 2; т — 1; ь - 1 P10(4,1,1,2,1,1)=___ 10! __= 75600                        4!·2!