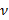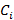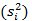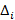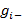2.1.1 Сравнение двух дисперсий. Цель сравнения дисперсий двух выборок  и
и 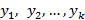 – ответ на вопрос, является ли различие выборочных дисперсий
– ответ на вопрос, является ли различие выборочных дисперсий 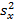 и
и 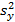 случайным, в то время как истинные дисперсии (т.е. дисперсии генеральных совокупностей) совпадают:
случайным, в то время как истинные дисперсии (т.е. дисперсии генеральных совокупностей) совпадают:  , или действительно
, или действительно 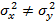 . Формально проверяется гипотеза о равенстве истинных дисперсий:
. Формально проверяется гипотеза о равенстве истинных дисперсий:  . Если генеральные совокупности распределены нормально, критерием является отношение:
. Если генеральные совокупности распределены нормально, критерием является отношение:

Отношение 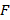 (
(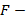 критерий) – случайная переменная, подчиняющаяся распределению Фишера, представленного на рисунке 7, с
критерий) – случайная переменная, подчиняющаяся распределению Фишера, представленного на рисунке 7, с 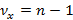 степенями свободы дисперсии в числителе и
степенями свободы дисперсии в числителе и 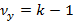 степенями свободы в знаменателе. Область значений
степенями свободы в знаменателе. Область значений 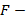 критерия
критерия 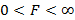 . Так как по смыслу задачи обе равноправны, то альтернативной проверяемой гипотезе является гипотеза
. Так как по смыслу задачи обе равноправны, то альтернативной проверяемой гипотезе является гипотеза 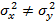 .
. 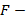 критерий может принимать любые значения из интервала
критерий может принимать любые значения из интервала 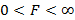 и является двусторонним – имеет две критические области. Но, всегда помещая в числитель отношения большую из двух дисперсий (т.е. считая
и является двусторонним – имеет две критические области. Но, всегда помещая в числитель отношения большую из двух дисперсий (т.е. считая  ), мы ограничиваем практическое применение критерия интервалом
), мы ограничиваем практическое применение критерия интервалом 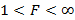 с единственной (правой) критической областью:
с единственной (правой) критической областью:

где  – уровень значимости
– уровень значимости 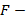 критерия.
критерия.
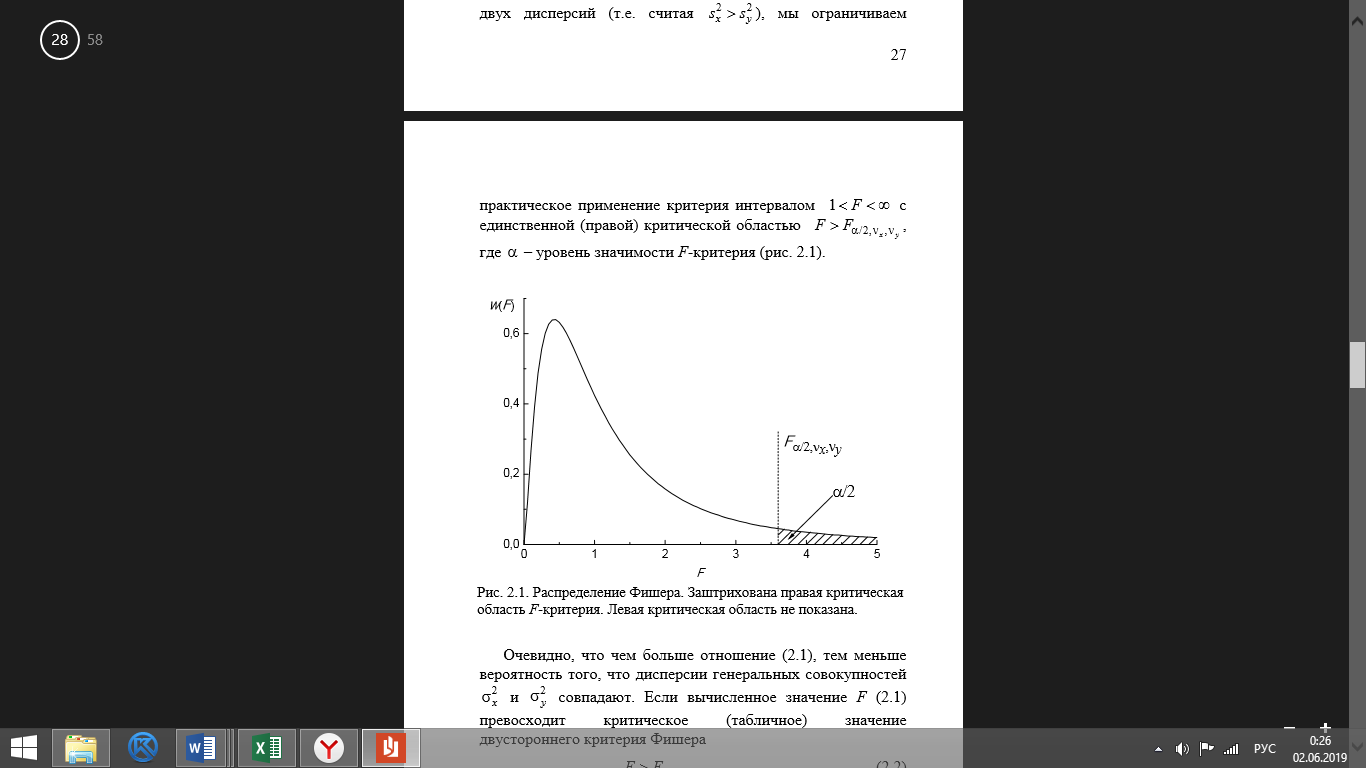
Рисунок 7 – Распределение Фишера (заштрихована правая критическая область F - критерия, левая критическая не показана)
Очевидно, что чем больше отношение, тем меньше вероятность того, что дисперсии генеральных совокупностей 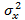 и
и  совпадают. Если вычисленное значение
совпадают. Если вычисленное значение 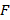 превосходит критическое (табличное) значение двустороннего критерия Фишера
превосходит критическое (табличное) значение двустороннего критерия Фишера  , то с риском ошибки не большим, чем
, то с риском ошибки не большим, чем  утверждается, что дисперсии генеральных совокупностей
утверждается, что дисперсии генеральных совокупностей 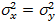 различны.
различны.
Иначе это формулируется: дисперсии 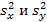 различаются значимо. Если знак неравенства противоположный, говорят, что дисперсии
различаются значимо. Если знак неравенства противоположный, говорят, что дисперсии 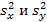 различаются незначимо.
различаются незначимо.
2.1.2 Сравнение двух средних. Сравнение средних  и
и 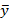 двух выборок
двух выборок  и
и 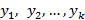 , как и сравнение дисперсий, отвечает на вопрос, различаются ли средние
, как и сравнение дисперсий, отвечает на вопрос, различаются ли средние  и
и 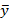 статистически значимо и тогда математические ожидания генеральных совокупностей различны:
статистически значимо и тогда математические ожидания генеральных совокупностей различны: 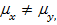 или различие выборочных средних случайно и
или различие выборочных средних случайно и 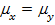 . Таким образом, проверяется гипотеза о равенстве математических ожиданий
. Таким образом, проверяется гипотеза о равенстве математических ожиданий  против альтернативной гипотезы об их неравенстве. При условии, что дисперсии
против альтернативной гипотезы об их неравенстве. При условии, что дисперсии 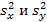 различаются незначимо (т.е. гипотеза
различаются незначимо (т.е. гипотеза 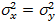 не противоречит наблюдениям) критерием здесь является функция:
не противоречит наблюдениям) критерием здесь является функция:

где свободная дисперсия
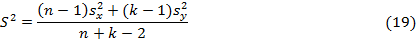
Критерий имеет t – распределение Стьюдента с  степенями свободы. Критерий двусторонний с двумя критическими областями
степенями свободы. Критерий двусторонний с двумя критическими областями 
 (рисунок 4). Но, поскольку
(рисунок 4). Но, поскольку 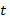 - распределение симметрично относительно нуля, на практике после замены
- распределение симметрично относительно нуля, на практике после замены 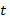 на
на 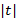 можно использовать только правую половину t – распределения, для которой и составляются таблицы. Если вычисленное значение t – критерия превосходит критическое (табличное) с уровнем значимости a и числом степеней свободы n
можно использовать только правую половину t – распределения, для которой и составляются таблицы. Если вычисленное значение t – критерия превосходит критическое (табличное) с уровнем значимости a и числом степеней свободы n  , то гипотеза о равенстве математических ожиданий
, то гипотеза о равенстве математических ожиданий  отклоняется с риском ошибки не большим, чем a. Иначе говорят, что средние
отклоняется с риском ошибки не большим, чем a. Иначе говорят, что средние  и
и 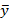 различаются значимо. Если знак неравенства противоположный, гипотеза о равенстве математических ожиданий не отклоняется, и различие средних
различаются значимо. Если знак неравенства противоположный, гипотеза о равенстве математических ожиданий не отклоняется, и различие средних  и
и 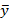 незначимо.
незначимо.
2.1.3 Несколько групп данных. Часто необходимо сравнить  групп данных с различным числом наблюдений в группах. Обозначим число наблюдений в
групп данных с различным числом наблюдений в группах. Обозначим число наблюдений в 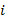 – той
– той  группе –
группе – 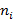 , а общее число наблюдений
, а общее число наблюдений 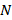 :
:  . Считаем, что данные в
. Считаем, что данные в 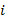 – той группе
– той группе 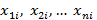 – независимая выборка из своей (
– независимая выборка из своей (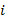 – той) нормально распределённой генеральной совокупности с математическим ожиданием
– той) нормально распределённой генеральной совокупности с математическим ожиданием  и истиной дисперсией
и истиной дисперсией  .
.
Выборочное среднее в группе:

Выборочная дисперсия:

Сравнение нескольких дисперсий (проверка гипотезы однородности дисперсий)
Сравнение дисперсий 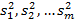 предполагает проверку гипотезы о том, что истинные дисперсии соответствующих нормальных генеральных совокупностей равны:
предполагает проверку гипотезы о том, что истинные дисперсии соответствующих нормальных генеральных совокупностей равны:  -
- 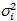 не равна всем остальным.
не равна всем остальным.
Проверочная статистика этой гипотезы (критерий Бартлетта) – отношение:

Числитель которого
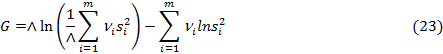
Где 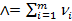 , а знаменатель
, а знаменатель
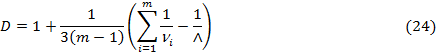
Если все  , критерий Бартлетта приближенно подчиняется c2 – распределению (распределению Пирсона) с
, критерий Бартлетта приближенно подчиняется c2 – распределению (распределению Пирсона) с 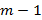 степенями свободы. Если величина критерия B больше критического значения B >
степенями свободы. Если величина критерия B больше критического значения B > 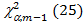 , то гипотеза однородности дисперсий отвергается с риском ошибки, не большим
, то гипотеза однородности дисперсий отвергается с риском ошибки, не большим  . Если знак неравенства противоположный, гипотеза однородности дисперсий не противоречит наблюдениям и не отвергается.
. Если знак неравенства противоположный, гипотеза однородности дисперсий не противоречит наблюдениям и не отвергается.
2.1.4 Сравнение нескольких средних (дисперсионный анализ). Оценка различий между средними в нескольких группах проводится методом дисперсионного анализа. В нем сравнивается разброс данных между группами с разбросом данных внутри групп.
При условии однородности дисперсий все дисперсии в группах 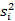 оценивают одну и ту же внутригрупповую дисперсию
оценивают одну и ту же внутригрупповую дисперсию  . Тогда все выборочные дисперсии
. Тогда все выборочные дисперсии 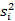 можно объединить, получив средний квадрат отклонений в группе (иначе – остаточную дисперсию) с числом степеней свободы
можно объединить, получив средний квадрат отклонений в группе (иначе – остаточную дисперсию) с числом степеней свободы 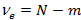
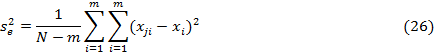
Остаточная дисперсия  – обобщенная оценка истинной внутригрупповой дисперсии
– обобщенная оценка истинной внутригрупповой дисперсии  , характеризующей разброс наблюдений внутри групп.
, характеризующей разброс наблюдений внутри групп.
При равенстве дисперсий  различие между группами проявляется в разнице математических ожиданий в группах
различие между группами проявляется в разнице математических ожиданий в группах  . Если все математические ожидания равны:
. Если все математические ожидания равны:  , то различия между группами нет. В этом случае все группы являются выборками из одной и той же (нормальной) генеральной совокупности с математическим ожиданием
, то различия между группами нет. В этом случае все группы являются выборками из одной и той же (нормальной) генеральной совокупности с математическим ожиданием 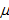 и дисперсией
и дисперсией  .
.
Различие между группами оценивается по разбросу средних в группах 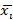 вокруг общего среднего
вокруг общего среднего 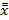 :
:

Поскольку дисперсия выборочного среднего по 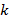 наблюдениям в
наблюдениям в 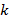 раз меньше дисперсии генеральной совокупности, то в оценке дисперсии между группами через выборочные средние
раз меньше дисперсии генеральной совокупности, то в оценке дисперсии между группами через выборочные средние 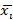 каждое слагаемое берется со своим множителем
каждое слагаемое берется со своим множителем 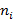 :
:

Величина 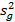 называется средним квадратом между группами или межгрупповой дисперсией; она характеризует разброс данных между группами. Число ее степеней свободы
называется средним квадратом между группами или межгрупповой дисперсией; она характеризует разброс данных между группами. Число ее степеней свободы 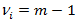 . Если гипотеза
. Если гипотеза  , верна, то разброс между группами наблюдений только случайный, дисперсия генеральной совокупности совпадает с внутригрупповой дисперсией
, верна, то разброс между группами наблюдений только случайный, дисперсия генеральной совокупности совпадает с внутригрупповой дисперсией  и оба средних квадрата
и оба средних квадрата 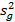 и
и 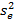 оценивают эту дисперсию. Если же реальное различие между группами существует (т.е. гипотеза
оценивают эту дисперсию. Если же реальное различие между группами существует (т.е. гипотеза  , не верна), то остаточная дисперсия
, не верна), то остаточная дисперсия 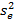 оценивает только дисперсию в группах, истинное значение которой, как и ранее равно
оценивает только дисперсию в группах, истинное значение которой, как и ранее равно  , а межгрупповая дисперсия
, а межгрупповая дисперсия 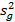 оценивает истинную межгрупповую дисперсию, значение которой больше, чем
оценивает истинную межгрупповую дисперсию, значение которой больше, чем  . Поскольку принята гипотеза нормального распределения в группах, оценку различия дисперсий
. Поскольку принята гипотеза нормального распределения в группах, оценку различия дисперсий  и
и 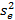 можно провести количественно, рассчитав
можно провести количественно, рассчитав  - критерий – отношение:
- критерий – отношение:

Критерий односторонний – альтернативная гипотеза (различия математических ожиданий в группах  ) предполагает, что дисперсия в числителе отношения больше дисперсии в знаменателе. Следовательно, если рассчитанное значение критерия превосходит критическое значение одностороннего критерия Фишера с уровнем значимости a и с числом степеней свободы дисперсии в числителе
) предполагает, что дисперсия в числителе отношения больше дисперсии в знаменателе. Следовательно, если рассчитанное значение критерия превосходит критическое значение одностороннего критерия Фишера с уровнем значимости a и с числом степеней свободы дисперсии в числителе  дисперсии в знаменателе
дисперсии в знаменателе 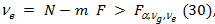 то гипотеза равенства математических ожиданий в группах
то гипотеза равенства математических ожиданий в группах 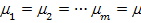 , противоречит наблюдениям с риском ошибки этого утверждения не больше, чем a. Иначе говоря, если дисперсия между группами значимо больше остаточной дисперсии, то средние в группах различаются значимо, т.е. изменение свойства Х между группами заметно на фоне его разброса внутри групп. При противоположном знаке неравенства гипотеза о равенстве математических ожиданий в группах
, противоречит наблюдениям с риском ошибки этого утверждения не больше, чем a. Иначе говоря, если дисперсия между группами значимо больше остаточной дисперсии, то средние в группах различаются значимо, т.е. изменение свойства Х между группами заметно на фоне его разброса внутри групп. При противоположном знаке неравенства гипотеза о равенстве математических ожиданий в группах 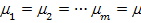 , не противоречит наблюдениям или средние в группах различаются незначимо.
, не противоречит наблюдениям или средние в группах различаются незначимо.
2.2 Практическая часть
Задание:
1) Имеются четыре группы данных 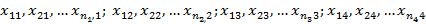 .
.
2) Рассчитать в группах выборочные средние 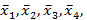 и выборочные дисперсии
и выборочные дисперсии 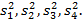
3) Для выборочных дисперсий 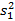 и
и 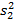 рассчитать значение F-критерия и, сравнив его с табличным значением с уровнем значимости a = 0,05, проверить гипотезу о значимом различии дисперсий.
рассчитать значение F-критерия и, сравнив его с табличным значением с уровнем значимости a = 0,05, проверить гипотезу о значимом различии дисперсий.
4) Для выборочных средних 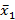 и
и 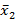 рассчитать значение t-критерия и, сравнив его с табличным значением с уровнем значимости a = 0,05, проверить гипотезу о значимом различии средних.
рассчитать значение t-критерия и, сравнив его с табличным значением с уровнем значимости a = 0,05, проверить гипотезу о значимом различии средних.
5) Для выборочных дисперсий в группах 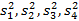 рассчитать значение критерия Бартлетта В, и сравнив его с табличным значением критерия s2 с уровнем значимости a = 0,05, проверить гипотезу однородности дисперсий.
рассчитать значение критерия Бартлетта В, и сравнив его с табличным значением критерия s2 с уровнем значимости a = 0,05, проверить гипотезу однородности дисперсий.
6) Провести дисперсионный анализ: рассчитать отношение дисперсии между группами к остаточной дисперсии, сравнить его со значением F-критерия с уровнем значимости a = 0,05 проверить гипотезу о значимом различии средних в группах.
7) Рассчитать доверительные интервалы истинных средних в группах с доверительной вероятностью 0,95. Построить диаграмму средних в группах с доверительными интервалами. Описать особенности диаграммы, если они есть.
Исходные данные представлены в таблице 2.
Таблица 2 – Исходные данные
| Высота по оси слитка | 1 | 2 | 3 | 4 |
| Плотность сульфидов мм-2 в стали 40Х | 12,1 | 16,2 | 22,2 | 30,7 |
| 15,5 | 7,6 | 12 | 12,1 | |
| 10,9 | 11,4 | 19,5 | 22,7 | |
| 21,9 | 18,1 | 20,5 | 18,7 | |
| 20,6 | 10,4 | 14,9 | 19,4 | |
| 11,3 | 11,4 | 11,8 | 9,1 | |
| 14,8 | 19,1 | 13,6 | 32,4 | |
| 12,7 | 2,0 | 22,2 | 11,1 | |
| 12,2 | 13,0 | 25,6 | 20,6 | |
| 17,1 | 9,0 | 20,4 | ||
| 13,3 |
1) Расчет выборочных средних и дисперсий
Число групп данных  . Рассчитывается число данных в каждой группе
. Рассчитывается число данных в каждой группе 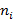 и число степеней свободы дисперсии в группах
и число степеней свободы дисперсии в группах
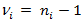
Вычисляется сумма и сумма квадратов для каждой группы:

Рассчитывается выборочные средние 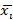 и выборочные дисперсии
и выборочные дисперсии 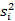 в группах
в группах

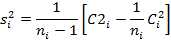
Рассчитанные значения представлены в таблице 3.
2) Проверка гипотезы о значимом различии дисперсий
Рассчитывается отношение дисперсий по формуле:
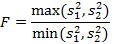
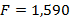
По данным представленным в приложении Г, определяется табличное значение 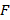 – критерия с уровнем значимости
– критерия с уровнем значимости 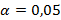
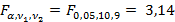
Проводится сравнение рассчитанного 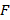 – критерия с табличным с применением двустороннего критерия Фишера (неравенство (17)).
– критерия с табличным с применением двустороннего критерия Фишера (неравенство (17)).
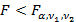
Вывод: с риском ошибки не большим 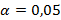 дисперсии
дисперсии 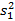 и
и 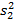 различаются незначимо.
различаются незначимо.
3) Проверка гипотезы о значимом различии средних
Для дисперсий 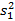 и
и 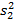 рассчитывается объединенная дисперсия
рассчитывается объединенная дисперсия 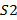 по формуле (19) и число ее степеней свободы
по формуле (19) и число ее степеней свободы

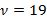
Рассчитывается по формуле (18) значение t – критерия
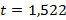
По данным представленным в приложении Б, определяется табличное значение 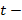 критерия с уровнем значимости
критерия с уровнем значимости 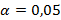
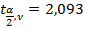
Проводится сравнение рассчитанного 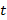 – критерия с табличным значением
– критерия с табличным значением 

Вывод: гипотеза о равенстве математических ожиданий отклоняется с риском ошибки небольшим 0,05 и средние 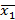 и
и  различаются значимо.
различаются значимо.
4) Проверка гипотезы однородности дисперсий
Предварительные вычисления проводятся по формулам: 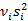 ;
; 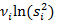 ;
; 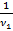 .
.
Вычисляются суммы 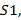
 :
:
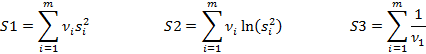

Рассчитывается общее число степеней свободы

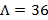
Рассчитывается числитель 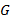 и знаменатель
и знаменатель 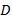 критерия Бартлетта
критерия Бартлетта 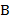 по формулам:
по формулам:


Критерий Бартлетта вычисляется по формуле (22).
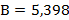
По данным, представленным в приложении В, определяется табличное значение критерия Пирсона с уровнем значимости 0,05 и числом степеней свободы 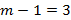 .
.

Проводится сравнение рассчитанного значения 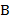 с табличным значением критерия Пирсона
с табличным значением критерия Пирсона 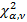 .
.
Вывод: гипотеза однородности дисперсий не отвергается и не противоречит наблюдениям.
Результаты расчетов представлены в таблице 3.
Рассчитывается общее число данных 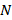 и общее среднее
и общее среднее 
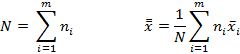


Рассчитывается остаточная дисперсия 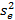 как взвешенная сумма дисперсий в группах
как взвешенная сумма дисперсий в группах
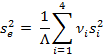

Рассчитывается квадраты отклонения групп от общего среднего 
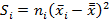
Рассчитанные значения  , представлены в таблице 3.
, представлены в таблице 3.
Рассчитывается дисперсия между группами 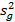
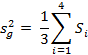
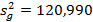
Вычисляется отношение дисперсий по формуле (29).
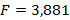
По данным, представленным в приложении Г, определяется табличное значение критерия Фишера с уровнем значимости 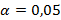 и числом степеней свободы
и числом степеней свободы 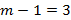 , дисперсии в знаменатели
, дисперсии в знаменатели 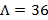 .
.
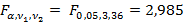
Проводится сравнение рассчитанного критерия Фишера 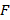 с табличным значением критерия Фишера
с табличным значением критерия Фишера 
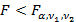
Вывод: гипотеза равенства математических ожиданий в группах не противоречит наблюдениям с риском ошибки утверждения не больше чем 0,05, то есть изменение свойства между группами различаются незначимо.
6) Построение диаграммы средних в группах с доверительными интервалами
В каждой группе рассчитывается полуширина доверительного интервала с доверительной вероятностью Р = 0,95

Значение 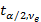 с уровнем значимости
с уровнем значимости 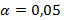 и числом степеней свободы 36 определяется по таблице представленной в приложение Б.
и числом степеней свободы 36 определяется по таблице представленной в приложение Б.

Рассчитывается нижние 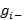 и верхние
и верхние 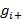 доверительные границы средних в группах
доверительные границы средних в группах

Рассчитанные значения представлены в таблице 3.
Таблица 3 – Результаты расчетов
| Группа | 1 | 2 | 3 | 4 |
| Данных в группе | 10 | 11 | 10 | 9 |
| 9 | 10 | 9 | 8 | |
| Сумма | 149,1 | 131,5 | 182,7 | 176,8 |
| Сумма квадратов | 2358,710 | 1811,590 | 3547,910 | 4010,380 |
| Средние | 14,910 | 11,955 | 18,270 | 19,644 |
| Дисперсия | 15,070 | 23,957 | 23,331 | 67,155 |
| ln | 2,713 | 3,176 | 3,150 | 4,207 |
|
| 135,629 | 239,567 | 209,981 | 537,242 |
|
| 24,414 | 31,762 | 28,348 | 33,656 |
|
| 0,111 | 0,100 | 0,111 | 0,125 |
| S1 | 1122,419 |
|
|
|
| S2 | 118,181 |
|
|
|
| S3 | 0,447 |
|
|
|
| Квадрат отклонения групп | 11,936 | 180,245 | 51,416 | 119,374 |
| Полуширина доверительного интервала | 2,481 | 2,983 | 3,087 | 5,521 |
| Нижняя доверительная граница | 12,429 | 8,972 | 15,183 | 14,124 |
| Верхняя доверительная граница | 17,391 | 14,937 | 21,357 | 25,165 |
Строится диаграмма изменчивости средних в группах, представленная на рисунке 8, с нанесениям средних с 95% - ными доверительными границами.
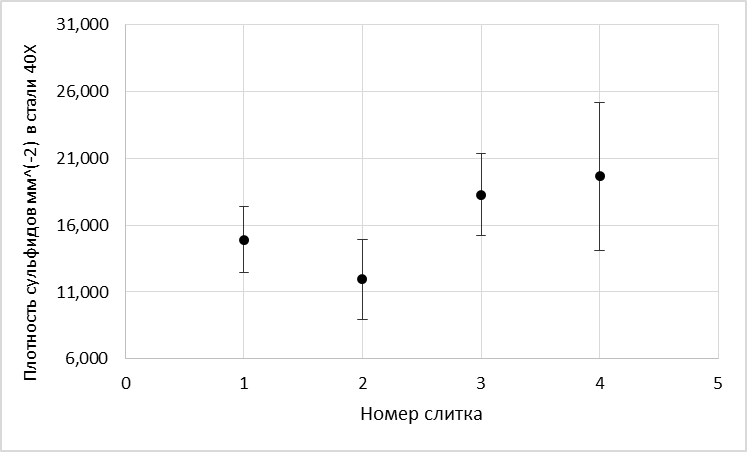
Рисунок 8 - Средние в группах с 95% доверительными интервалами для математических ожиданий
 2020-08-05
2020-08-05 1763
1763