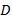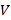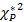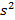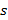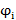Парный коэффициент корреляции и эллипс рассеяния

 

3.1 Теоретические сведения

 

3.1.1 Выборочный парный коэффициент корреляции. Пусть имеются выборки двух случайных нормально распределенных переменных X и Y – , и каждая пара,  (n = 1, 2 … n) получена в идентичных условиях, например,  – два свойства материала, измеренные в одном (i - том) эксперименте. Случайные переменные X и Y могут изменяться взаимосвязано, так, что с возрастанием одной переменной возрастает (или убывает) вторая. Такое изменение можно заметить на диаграмме, представленной на рисунке 9, рассеяния – точечном графике, на котором результаты экспериментов изображаются точками в плоскости с координатными осями x и y.

Если переменные X и Y изменяются закономерно, то точки на графике расположены не хаотично во всей области изменения переменных, а группируются около наклонной прямой.

 

Рисунок 9 - Диаграмма рассеяния двух случайных переменных и эмпирический эллипс рассеяния

 

Количественно степень близости экспериментальных точек к прямой линии, т.е. силу линейной взаимосвязи случайных переменных X и Y, характеризует выборочный парный коэффициент корреляции:

 

 

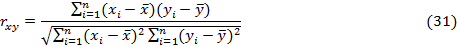
где, 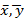– выборочные средние выборок  и .

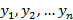Парный коэффициент корреляции изменяется в пределах: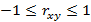

Чем ближе 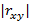 к единице, тем плотнее точки на точечном графике группируются около наклонной прямой линии, тем сильнее (на фоне случайного разброса) выражена линейная связь переменных X и Y. Если 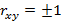, то линейная связь является функциональной и точки ложатся строго на прямую. Условие  означает, что переменные X и Y изменяются в одном направлении, условие 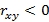– что они изменяются противоположных направлениях. Если 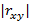близок к нулю, то взаимосвязанного изменения случайных переменных X и Y нет, и точки на диаграмме рассеяния расположены хаотично. Величина парного коэффициента корреляции  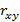не изменится, если каждое значение любой из выборок  , 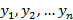умножить на произвольное число или прибавить ко всем значениям произвольное число.

Поскольку значения  ,  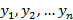являются выборочными, случайная группировка точек вокруг прямой линии может получиться и тогда, когда переменные X и Y на самом деле не коррелированны. Чтобы убедиться, что рассчитанный парный коэффициент корреляции  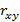не случайно отличается от нуля, проверяют гипотезу о значимом отличии 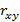от нуля. Значение  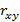сравнивают с критическим (табличным) значением выборочного коэффициента корреляции  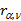 с уровнем значимости a и числом степеней свободы  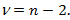Если 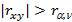 (32), то с риском ошибки, не большим a считается, что выборочный парный коэффициент корреляции 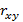отличается от нуля не случайно (значимо отличается от нуля) и отражает действительную тенденцию взаимосвязанного изменения переменных X и Y. Если знак неравенства противоположный, то нет достаточных оснований утверждать, что отличие коэффициента корреляции 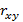от нуля не случайное. В этом случае говорят, что парный коэффициент корреляции  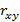незначимо отличается от нуля (коэффициент незначимый).

3.1.2 Эмпирический эллипс рассеяния. Множеству наблюдений  (n = 1, 2 … n) можно сопоставить эмпирический эллипс рассеяния. Если случайные переменные X и Y распределены нормально, то внутрь эллипса попадает в среднем доля Р всех наблюдений (вероятность попадания точки  , внутрь эллипса равна P). Центр эллипса имеет координаты (, т.е. находится в центре тяжести точек  .Форма и размеры эллипса определяются величинами стандартных отклонений выборок 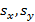 парного коэффициента корреляции  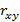и заданной вероятностью Р. Уравнение эллипса рассеяния:

 

 

где 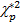 - квантиль распределения Пирсона (c² - распределения) с двумя степенями свободы. Если распределения случайных переменных X и Y не слишком отличаются от нормального, эмпирический эллипс рассеяния дает наглядное представление о совместной области рассеяния данных.

Чтобы построить эллипс рассеяния надо перейти к новым переменным, т.к. рассчитывать координаты точек эллипса непосредственно по уравнению эллипса рассеяния неудобно. Для расчета сначала перейдем к стандартизованным безразмерным переменным – центрируем исходные переменные и нормируем их на стандартные отклонения соответствующих выборок:

 

Затем введем новые переменные u и n, координатные оси которых совпадают с главными осями эллипса рассеяния:

 

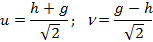
В переменных u и n уравнение эллипса рассеяния примет вид:

 

 

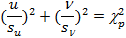
где стандартные отклонения переменных u и n равны 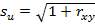 (34.1) и  соответственно.

 

Точки на эллипсе рассчитываются из параметрического уравнения эллипса:

 

где 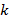 – коэффициент размера эллипса: ;

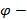 параметр .

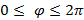После расчета точек на эллипсе в переменных u и n по параметрическому уравнению их координаты преобразуются к исходным переменным х и у по формулам:

 

 

 

 

3.2 Практическая часть

 

Задание:

1) По наблюдениям,  (n=1,2…n) рассчитать выборочный парный коэффициент корреляции 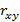, сравнить его с табличным значением с уровнем значимости a=0,05, проверить гипотезу о значимом отличии коэффициента корреляции  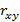от нуля.

2) По 12 точкам рассчитать эллипс рассеяния наблюдений, с вероятностью попадания внутрь эллипса P=0,95. Построить точечный график наблюдений, , нанести на него эллипс рассеяния. Отметить особенности данных, если они есть.

 

 

Исходными данными для расчета выборочного парного коэффициента корреляции и построения эллипса рассеяния являются значения:

х: 98,2; 73,6; 85,0; 75,3; 78,4; 95,2; 97,7; 65,9; 85,3; 74,0; 77,2; 83,4; 71,4; 88,5; 80,0; 76,3; 82,9; 84,2; 90,6; 57,6; 75,3; 90,4; 69,2; 88,8; 82,3; 70,6.

Количество данных

у: 45,8; 37,1; 39,6; 41,9; 31,7; 39,4; 40,3; 36,6; 42,2; 36,3; 33,1; 37,9; 32,7; 31,3; 34,24 40,4; 30,8; 31,9; 37,9; 31,5; 38,7; 32,4; 37,2; 34,9; 41,7; 29,9.

Количество данных

 

1) Определение выборочного парного коэффициента корреляции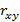

Вычисляются суммы:

 

 

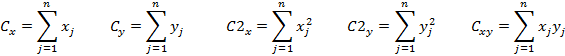
Рассчитываются среднее:

 

 

Проводится расчет промежуточных значений:

 

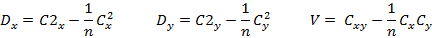
Выборочный парный коэффициент корреляции :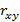

 

 

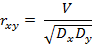
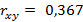
По таблице, представленной в приложении Д, определяется критическое значение коэффициента корреляции  с уровнем значимости 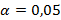 и числом степеней свободы .

 

 

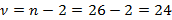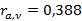
Сравним выборочный парный коэффициент корреляции с критическим значением коэффициента корреляции

 

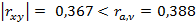
Вывод: выборочный парный коэффициент корреляции 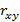 меньше критического значения коэффициента корреляции , следовательно, нет достаточных оснований утверждать, что отличие коэффициента корреляции от нуля не случайное, то есть парный коэффициент корреляции незначимо отличается от нуля (коэффициент незначимый).

По исходным данным строится диаграмма рассеяния, представленная на рисунке 10.

 

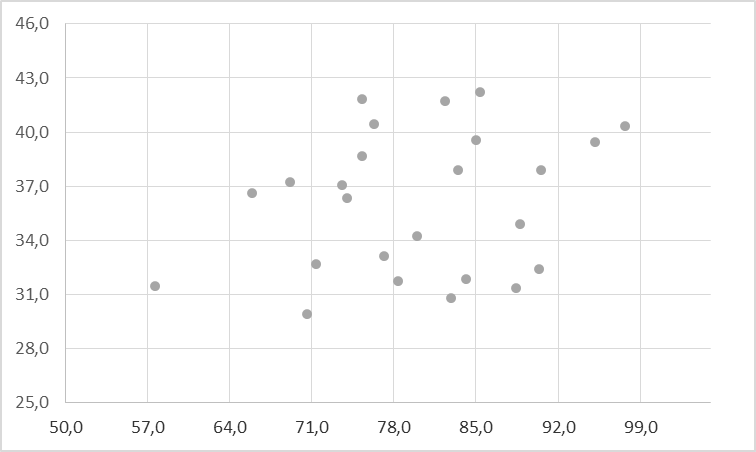
Рисунок 10 – Диаграмма рассеяния

 

2) Построение эллипса рассеяния

Вычисляются дисперсии и стандартные отклонения:

 

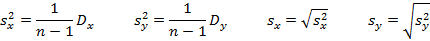
По формулам (34.1) и (34.2) рассчитываются стандартные отклонения 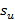 и .

 

 

 

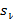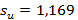
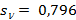
По таблице, представленной в приложении В, определяется квантиль распределения Пирсона для вероятности попадания наблюдения внутрь эллипса Р = 0,95 с двумя степенями свободы.

Рассчитывается коэффициент размера эллипса по формуле:

 

Рассчитанные значения представлены в таблице 4.

 

Таблица 4 – Рассчитанные значения

	x	y	ху
Сумма	2097	948	76825,00
Суммы квадратов	171606,3	34997,1
Среднее	81	36
Промежуточные вычисление	2453,89	456,25
Промежуточное			388,14
Квантиль распределения Пирсона	5,991
Коэффициент размера эллипса	2,448
Дисперсия	98,16	18,25
Стандартные отклонения	9,91	4,27

 

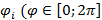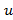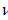Рассчитываем 12 значений параметра ) с шагом , далее рассчитываются значения  и . По формулам (35.1) и (35.2) рассчитываются координаты  и . По формулам (36.1) и (36.2) рассчитывается х и у точек эллипса.

Значения, рассчитанные для построения эллипса рассеяния представлены в таблице 5.

 

 

Таблица 5 – Данные для построения эллипса рассеяния

параметр	cos()	sin()	u эллипса	v эллипса	x эллипса	y эллипса
0,000	1,000	0,000	2,862	0,000	100,707	45,093
0,524	0,866	0,500	2,478	0,974	91,198	46,877
1,047	0,500	0,866	1,431	1,687	78,866	45,866
1,571	0,000	1,000	0,000	1,948	67,014	42,332
2,094	-0,500	0,866	-1,431	1,687	58,818	37,222
2,618	-0,866	0,500	-2,478	0,974	56,475	31,904
3,142	-1,000	0,000	-2,862	0,000	60,611	27,804
3,665	-0,866	-0,500	-2,478	-0,974	70,120	26,020
4,189	-0,500	-0,866	-1,431	-1,687	82,452	27,031
4,712	0,000	-1,000	0,000	-1,948	94,304	30,565
5,236	0,500	-0,866	1,431	-1,687	102,500	35,675
5,760	0,866	-0,500	2,478	-0,974	104,843	40,993
6,283	1,000	0,000	2,862	0,000	100,707	45,093

 

На диаграмму рассеяния наносятся координаты х и у точек эллипса и строится эмпирический эллипс рассеяния, представленный на рисунке 11.

 

Рисунок 11 – Диаграмма рассеяния двух случайных переменных и эмпирический эллипс рассеяния

 

 

 

Заключение

 

В данном курсовом проекте рассмотрены следующие разделы курса «Анализ данных в материаловедении»: первичный анализ экспериментальных данных, сравнение средних и дисперсий, парный коэффициент корреляции и эллипс рассеяния.

При выполнении первичного анализа экспериментальных данных произведена интервальная оценка среднего, построена гистограмма распределения выборки, построен график нормального распределения, проверена гипотеза нормального распределения экспериментальных данных.

При выполнении сравнения средних и дисперсий проверены гипотеза о значимом различии дисперсий и значимом различии средних для двух групп данных, проведен дисперсионный анализ и проверена гипотеза однородности дисперсий для 4 групп данных, проверена гипотеза о значимом различии средних в группах, также построена диаграмма средних в группах с 95%-процентными доверительными границами.

При выполнении расчета парного коэффициента корреляции и построения эллипса рассеяния проверена гипотеза о значимом отличии коэффициента корреляции от нуля, построены диаграмма рассеяния двух случайных переменных и эллипс рассеяния.