Введение
В металлургии и материаловедении большинство характеристик материалов и процессов измеримы. Целью данного курсового проекта является решение статистических задач в материаловедении, наиболее часто встречаемых на практике. К таким задачам относят: описательная статистика, проверка нормальности распределения экспериментальной величины, сравнение средних и дисперсий, дисперсионный анализ, построение и анализ диаграмм рассеяния и расчет парного коэффициента корреляции.
Курсовой проект состоит из трех разделов: первичный анализ экспериментальных данных, сравнение средних и дисперсий, парный коэффициент корреляции и эллипс рассеяния. Каждый раздел включает теоретические сведения, в которых подробно описывается рассматриваемая тема, и практическую часть, в которой подробно описан процесс выполнения поставленной задачи.
Первичный анализ экспериментальных данных
1.1 Теоретические сведения
1.1.1 Характеристики случайной величины. Результаты эксперимента или производственного контроля не являются полностью предсказуемыми, даже если известны значения всех факторов. В результатах всегда присутствует элемент неопределенности. С точки зрения теории вероятностей результат эксперимента или контроля является случайным событием, а сам эксперимент или производственный контроль - статистическим испытанием. Если случайное событие выражается числом, то такое число считается случайной величиной. Случайный - не означает «какой угодно». Каждое случайное событие Х происходит с некоторой вероятностью Р(Х).
Если регистрируемая в эксперименте случайная величина Х может (по крайней мере, теоретически) принимать любое произвольное значение на отрезке или числовой оси, то она называется непрерывной. Число возможных значений непрерывной случайной величины несчетно. Поэтому вероятность принять какое-либо конкретное значение х равна нулю: P (X = х) = 0 или P(x) = 0. Вместо этой вероятности можно определить вероятность попадания непрерывной случайной величины Х в интервал (x1; x2]:

Функция w(x), представленная на рисунке 1, называется плотностью распределения вероятности (или плотностью распределения или плотностью вероятности). Вероятность можно представить графически как заштрихованную площадь на рисунке 1. Функция плотности распределения нормирована так, что полная площадь под кривой w(x), т.е. вероятность того, что случайная величина Х примет какое-либо значение из интервала (-  ;
;  ) - P(-
) - P(-  < X <
< X <  ) - равна 1. График плотности распределения дает наглядное представление о том, как часто встречаются различные значения случайной величины Х.
) - равна 1. График плотности распределения дает наглядное представление о том, как часто встречаются различные значения случайной величины Х.

Рисунок 1 - Плотность распределения непрерывной случайной величины
Функция  (2) называется функцией распределения. Функция F(х) вычисляет вероятность P = F (х) того, что случайная величина Х принимает значение, меньшее или равное х, а обратная функция распределения по вероятности P = F(х) рассчитывает значение аргумента функции распределения х. Функция распределения, представленная на рисунке 2, - это неубывающая функция, такая, что F(-
(2) называется функцией распределения. Функция F(х) вычисляет вероятность P = F (х) того, что случайная величина Х принимает значение, меньшее или равное х, а обратная функция распределения по вероятности P = F(х) рассчитывает значение аргумента функции распределения х. Функция распределения, представленная на рисунке 2, - это неубывающая функция, такая, что F(-  ) = 0 и F(
) = 0 и F( ) = 1. Плотность вероятности w(х), как и функция распределения F(х) полностью определяют свойства непрерывной случайной величины.
) = 1. Плотность вероятности w(х), как и функция распределения F(х) полностью определяют свойства непрерывной случайной величины.
|
|
Рисунок 2 - Функция распределения непрерывной случайной величины
Некоторые наиболее важные свойства распределения случайной величины можно описать числовыми характеристиками распределения. Первая из них - математическое ожидание  (иначе первый момент распределения) - характеристика расположения центра распределения случайной величины. Математическое ожидание непрерывной случайной величины Х с плотностью вероятности w(x)
(иначе первый момент распределения) - характеристика расположения центра распределения случайной величины. Математическое ожидание непрерывной случайной величины Х с плотностью вероятности w(x)

Если распределения случайных величин X и Y различаются единственно их математическими ожиданиями  и
и  , то графики функций распределения или плотностей вероятностей одинаковые по форме, но сдвинуты один относительно другого на величину
, то графики функций распределения или плотностей вероятностей одинаковые по форме, но сдвинуты один относительно другого на величину  .
.
Характеристикой разброса случайной величины вокруг ее математического ожидания является дисперсия (иначе второй центральный момент). Дисперсия  непрерывной случайной величины Х:
непрерывной случайной величины Х:

Кроме дисперсии характеристикой разброса является и квадратный корень из нее – стандартное отклонение:

Стандартное отклонение  имеет ту же размерность, что и сама случайная величина Х (а дисперсия – квадрат этой размерности), поэтому оно удобнее для практической оценки разброса.
имеет ту же размерность, что и сама случайная величина Х (а дисперсия – квадрат этой размерности), поэтому оно удобнее для практической оценки разброса.
Другими важными характеристиками распределения непрерывной случайной величины являются квантили.
Квантилем  случайной величины X с функцией распределения F (х) называется значение случайной величины, для которого функция распределения принимает значение Р: F (
случайной величины X с функцией распределения F (х) называется значение случайной величины, для которого функция распределения принимает значение Р: F ( ) = P. На рисунке 2 показан квантиль
) = P. На рисунке 2 показан квантиль  , называемый медианой, и имеющий специальное обозначение тх. Вероятность того, что случайная величина окажется меньше медианы равна вероятности того, что она окажется больше медианы и равна 0,5. В прикладной статистике часто применяется квантиль
, называемый медианой, и имеющий специальное обозначение тх. Вероятность того, что случайная величина окажется меньше медианы равна вероятности того, что она окажется больше медианы и равна 0,5. В прикладной статистике часто применяется квантиль  , вероятность превышения которого равна 0,05.
, вероятность превышения которого равна 0,05.
1.1.2 Нормальное распределение. Нормальное распределение занимает центральное место в теоретической статистике. Нормальное распределение возникает, когда разброс наблюдаемой величины вызван множеством причин, каждая из которых вносит в этот разброс вклад, сравнимый с вкладом других причин, и нет единственной преобладающей причины. Большинство методов статистического анализа применимо только к выборкам из нормальных генеральных совокупностей.
Плотность вероятности

Область определения -  <х <
<х <  .
.
Параметры распределения  и
и  >0 являются математическим ожиданием и стандартным отклонением нормально распределенной случайной величины.
>0 являются математическим ожиданием и стандартным отклонением нормально распределенной случайной величины.
Математическое ожидание  .
.
Дисперсия  .
.
Медиана  .
.
Нормальное распределение симметрично относительно математического ожидания  , поэтому значения медианы и математического ожидания совпадают. График нормального распределения с параметрами
, поэтому значения медианы и математического ожидания совпадают. График нормального распределения с параметрами  = 0 и
= 0 и  = 1 приведен на рисунке 3.
= 1 приведен на рисунке 3.

Рисунок 3 - Плотность вероятности нормального распределения с  = 0 и
= 0 и  = 1
= 1
Пусть  - вероятность того, что нормально распределенная случайная величина X находится в интервале (
- вероятность того, что нормально распределенная случайная величина X находится в интервале ( -
-  ;
;  +
+  ), тогда:
), тогда:



Следовательно, менее 1/3 значений нормально распределенной случайной величины отклоняется от математического ожидания более чем на одно стандартное отклонение.
Вероятность отклонения нормально распределенной случайной величины от математического ожидания более чем на два стандартных отклонения не превышает 0,0455, а на три стандартных отклонения - 0,0027.
1.1.3 Выборочные оценки. Результаты эксперимента - наблюдения x1, x2,..., xn, полученные в n повторных испытаниях, проведенных в идентичных условиях, - считаются значениями, принимаемыми в эксперименте измеряемой случайной величиной X. Все возможные значения случайной величины Х, распределенные с плотностью вероятности w(x) или функцией распределения F(x), называются генеральной совокупностью. Числовые характеристики распределения считаются параметрами генеральной совокупности. В математической статистике эксперимент интерпретируется как случайный выбор конкретного значения из бесконечной генеральной совокупности. Множество результатов xi, x2,..., xn - это случайная выборка из генеральной совокупности.
Генеральная совокупность является абстрактным понятием. Чтобы выборка полностью отражала свойства генеральной совокупности, она должна быть бесконечной. (Поэтому генеральную совокупность еще определяют, как бесконечное множество значений результатов статистического испытания, которое может при идентичных условиях повторяться сколь угодно большое число раз). Конечная выборка лишь приближенно с большей или меньшей точностью отражает свойства генеральной совокупности. По выборке можно оценить параметры генеральной совокупности и построить приближенную функцию распределения. Величины, рассчитанные по выборке, называются выборочными оценками параметров генеральной совокупностиили просто оценками.
Простейшие выборочные оценки параметров генеральной совокупности - точечные оценки. Точечная оценка - оценка параметра генеральной совокупности одним числом.
Точечная оценка математического ожидания  по случайной выборке x1, x2,...,xn - выборочное среднее:
по случайной выборке x1, x2,...,xn - выборочное среднее:

Точечная оценка дисперсии  при условии, что среднее x определено из тех же n наблюдений - выборочная дисперсия:
при условии, что среднее x определено из тех же n наблюдений - выборочная дисперсия:

Величина, стоящая в знаменателе, - число степеней свободы (ч.с.с.) выборочной дисперсии. В общем случае ч.с.с. дисперсии — это число наблюдений минус число линейных зависимостей между этими наблюдениями, использованных в расчете дисперсии (в данном случае одна зависимость для среднего).
Квадратный корень из выборочной дисперсии - выборочное стандартное отклонение - оценка стандартного отклонения генеральной совокупности  :
:

Для оценки выборочной медианы mx выборка x1, x2,..., xn сначала перестраивается в порядке возрастания (перестраивается в вариационный ряд). За выборочную медиану принимается средний по порядку член вариационного ряда (член с номером (n +1)/2) если n нечетное:

или полусумма двух расположенных в середине вариационного ряда чисел, если n четное:

Недостаток точечной оценки в том, что из нее не видно, насколько отличается оценка от истинного значения параметра генеральной совокупности. Интервальная оценка определяет границы интервала, в который истинное значение параметра генеральной совокупности попадает с заданной вероятностью Р, называемой доверительной. Очевидно, что эта вероятность должна быть достаточно большой: P = 0,9 или P = 0,95.
Наиболее употребительна интервальная оценка математического ожидания  . Она основана на том, что величина
. Она основана на том, что величина

подчиняется распределению Стьюдента с  степенями свободы (ч.с.с. дисперсии
степенями свободы (ч.с.с. дисперсии  ). Выберем доверительную вероятность Р, и пусть
). Выберем доверительную вероятность Р, и пусть  . Плотность распределения Стьюдента ws(t), представленная на рисунке 4, симметрична относительно t = 0, поэтому найдем положительное значение
. Плотность распределения Стьюдента ws(t), представленная на рисунке 4, симметрична относительно t = 0, поэтому найдем положительное значение  , такое, что случайная величина Т находится в интервале (
, такое, что случайная величина Т находится в интервале ( ) с вероятностью Р. Тогда математическое ожидание
) с вероятностью Р. Тогда математическое ожидание  с той же доверительной вероятностью Р находится внутри доверительного интервала
с той же доверительной вероятностью Р находится внутри доверительного интервала  , где
, где  (11)
(11)

Рисунок 4 - Плотность распределения Стьюдента c 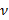 степенями свободы.
степенями свободы.
Заштрихованы периферийные области с суммарной вероятностью

При первичном анализе данных кроме точечных и интервальных оценок рассчитывается и строится гистограмма распределения, дающая наглядное представление о распределении данных. Для этого диапазон изменения выборки разбивается на m равных интервалов и подсчитывается число данных в каждом интервале n, n2..., nm. Далее строится график, обычно столбчатая диаграмма, где границы интервалов откладываются по горизонтальной оси, а величины  - по вертикальной.
- по вертикальной.
1.1.4 Проверка вида распределения. Часто необходимо проверить гипотезу о том, что анализируемая выборка x1, x2,..., xn является выборкой из генеральной совокупности с некоторым известным распределением. Проверка гипотез о виде распределения проводится с помощью критериев согласия. Как и другие статистические критерии, эти критерии отвечают на вопрос, противоречит ли выдвинутая гипотеза наблюдениям или не противоречит.
Универсальным критерием для проверки гипотезы о виде распределения является критерий Пирсона (x2 - критерий). Для применения этого критерия диапазон изменения выборки x1, x2,..., xn разбивают на m интервалов и рассчитывают количество попаданий данных в каждый интервал.

По этой же выборке оценивают параметры проверяемого распределения с плотностью вероятности w(x). Далее вычисляют вероятность попадания случайной величины Х в каждый интервал:

где  - левая и правая границы j-го интервала.
- левая и правая границы j-го интервала.
Взвешенная сумма квадратов разностей между наблюдаемым числом попаданий данных в интервал -  и рассчитанным по проверяемому распределению числом попаданий -
и рассчитанным по проверяемому распределению числом попаданий - 

Эта сумма является случайной величиной, подчиняющейся распределению Пирсона с числом степеней свободыv = m - l -1 (13), где l - количество оцененных по выборке параметров распределения. Чем больше различаются наблюдаемые nj и вычисленные по распределению npj числа данных в интервалах, тем больше величина критерия  и тем меньше шансов на то, что выборка x1, x2,..., xn взята из проверяемого распределения.
и тем меньше шансов на то, что выборка x1, x2,..., xn взята из проверяемого распределения.
Для любого положительного  можно вычислить вероятность p(
можно вычислить вероятность p( ) того, что случайная величина, имеющая распределение Пирсона, превосходит значение
) того, что случайная величина, имеющая распределение Пирсона, превосходит значение  .
.
Вероятность p( ) монотонно убывает с возрастанием величины
) монотонно убывает с возрастанием величины  , Следовательно, можно решить и обратную задачу – попаданной вероятности
, Следовательно, можно решить и обратную задачу – попаданной вероятности  найти такое значение
найти такое значение  , что
, что  .Индекс v указывает, что распределение критерия
.Индекс v указывает, что распределение критерия  зависит еще и от числа степенней свободы v. Величины
зависит еще и от числа степенней свободы v. Величины  приводятся в таблицах критических значений (иначе, процентных точек)
приводятся в таблицах критических значений (иначе, процентных точек)  -распределения. Пусть вычисленное в значение
-распределения. Пусть вычисленное в значение  превосходит некоторое табличное значение
превосходит некоторое табличное значение  (попадает в критическую область)
(попадает в критическую область)

Тогда при условии, что выборка х1, x2,..., xn принадлежит проверяемому распределению, вероятность получить такое значение критерия  будет меньше, чем
будет меньше, чем  :
:

Если заданная вероятность а мала, например,  = 0,05 или 0,01, то и вероятность выполнения неравенства при условии, что выборка x1, x2,...,xn взята из проверяемого распределения, мала. Тогда гипотеза о принадлежности выборки x1, x2,..., xn проверяемому распределению признается недостоверной и отвергается, т.е. делается вывод, что выборка x1, x2,...,xn не принадлежит проверяемому распределению. При этом остается риск ошибки такого вывода, не больший, чем
= 0,05 или 0,01, то и вероятность выполнения неравенства при условии, что выборка x1, x2,...,xn взята из проверяемого распределения, мала. Тогда гипотеза о принадлежности выборки x1, x2,..., xn проверяемому распределению признается недостоверной и отвергается, т.е. делается вывод, что выборка x1, x2,...,xn не принадлежит проверяемому распределению. При этом остается риск ошибки такого вывода, не больший, чем  . Эта заданная (малая) вероятность ошибки, а называется уровнем значимости критерия.
. Эта заданная (малая) вероятность ошибки, а называется уровнем значимости критерия.
При противоположном знаке неравенства меняется и знак неравенства. Тогда риск ошибочного отклонения гипотезы о принадлежности выборки проверяемому распределению считается достаточно большим, и проверяемая гипотеза не отклоняется.
Уровни значимости статистических критериев обычно выбираются из интервала 0,1 >  > 0,01. При малых величинах уровня значимости,
> 0,01. При малых величинах уровня значимости,  (малом риске ошибки, больших табличных значениях
(малом риске ошибки, больших табличных значениях  ) критерий будет реагировать только на большие отклонения выборочного распределения от теоретического. Проверяемая гипотеза о виде распределения будет отклоняться редко, и недостоверная гипотеза будет отклоняться с меньшей вероятностью. При более высоких значениях риска
) критерий будет реагировать только на большие отклонения выборочного распределения от теоретического. Проверяемая гипотеза о виде распределения будет отклоняться редко, и недостоверная гипотеза будет отклоняться с меньшей вероятностью. При более высоких значениях риска  (меньших табличных значениях
(меньших табличных значениях  ) критерий будет более чувствителен к малым отклонениям выборочного распределения от теоретического. Проверяемая гипотеза будет отклоняться чаще, и возрастет вероятность отклонения верной гипотезы. Наиболее употребителен уровень значимости
) критерий будет более чувствителен к малым отклонениям выборочного распределения от теоретического. Проверяемая гипотеза будет отклоняться чаще, и возрастет вероятность отклонения верной гипотезы. Наиболее употребителен уровень значимости  = 0,05. Логика применения других (рассмотренных ниже) статистических критериев аналогична.
= 0,05. Логика применения других (рассмотренных ниже) статистических критериев аналогична.
К разбиению выборки на интервалы для применения критерия Пирсона предъявляются определенные требования. Диапазон изменения выборки желательно разбивать на семь и более интервалов, так чтобы в каждом было не менее пяти наблюдений. При этом интервалы могут иметь разный размер; наилучшим является разбиение, при котором в каждый интервал попадает одинаковое число данных. При этом границы каждого интервала необходимо определять индивидуально. Вместо применения этой трудоемкой процедуры ограничиваются только объединением соседних интервалов, если в одном из них менее пяти данных. Кроме того, левая граница первого содержащего данные интервала расширяется до -∞, ∞ правая граница последнего содержащего данные интервала расширяется до ∞.
1.2 Практическая часть
Задание:
1) Рассчитать точечные оценки: выборочное среднее  , дисперсию
, дисперсию  и стандартное отклонение sx.
и стандартное отклонение sx.
2) Определить выборочную медиану распределения mx.
3) Произвести интервальную оценку среднего - построить доверительный интервал для истинного среднего с доверительной вероятностью P = 0,95.
4) Определить размер интервала разбиения, вычислить границы интервалов, рассчитать число попаданий в каждый интервал и построить гистограмму распределения выборки.
5) Нанести на гистограмму график проверяемого нормального распределения, сравнить вид проверяемого распределения и экспериментальной гистограммы.
6) Для нормального распределения с параметрами  и sx рассчитать значение критерия
и sx рассчитать значение критерия  и, сравнив его с табличным значением с уровнем значимости
и, сравнив его с табличным значением с уровнем значимости  = 0,05, проверить гипотезу о нормальном распределении экспериментальных данных.
= 0,05, проверить гипотезу о нормальном распределении экспериментальных данных.
Исходными данными для первичного анализа экспериментальных данных являются значения:
18,5; 20,5; 19,5; 22; 22,5; 20,5; 22; 23; 21,5; 21; 21; 21,5; 20,5; 18,5; 23,5; 21; 19; 22,5; 20,5; 23,5; 22,5; 21; 22; 22,5; 19; 22,5; 24,5; 21; 24,5; 21,5; 21; 21,5; 21,5; 20; 24; 25; 20; 18; 22,5; 22; 20,5; 21,5; 23; 23; 21; 21; 21,5; 22,5; 21; 20; 19; 19; 20,5; 20,5; 21,5; 21; 21; 21; 21,5; 21,5; 21; 21,5; 20; 20; 22; 19,5; 22; 22,5; 21,5; 21; 21; 21; 21,5; 21; 21,5; 20; 21; 20,5; 21; 22; 21,5; 21,5; 21; 20; 21,5; 22,5; 22; 20,5; 19,5; 21; 23; 20; 23,5; 22,5; 19,5; 20; 20,5; 23,5.
Количество данных 
1) Точечная оценка
Вариационный ряд данных перестраивается по возрастанию:
18; 18,5; 18,5; 19; 19; 19; 19; 19,5; 19,5; 19,5; 19,5; 20; 20; 20; 20; 20; 20; 20; 20; 20; 20,5; 20,5; 20,5; 20,5; 20,5; 20,5; 20,5; 20,5; 20,5; 20,5; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 21,5; 22; 22; 22; 22; 22; 22; 22; 22; 22,5; 22,5; 22,5; 22,5; 22,5; 22,5; 22,5; 22,5; 22,5; 22,5; 23; 23; 23; 23; 23,5; 23,5; 23,5; 23,5; 24; 24,5; 24,5; 25.
Рассчитываются суммы  и
и  :
:


Рассчитывается среднее значение  , а также дисперсия
, а также дисперсия 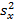 и стандартное отклонение
и стандартное отклонение  :
:



2) Определение выборочной медианы распределения 
Так как  – четное, то за выборочную медиану распределения принимается член вариационного ряда определяемый по формуле 10.2.
– четное, то за выборочную медиану распределения принимается член вариационного ряда определяемый по формуле 10.2.
Определяется максимальное и минимальное значение х.
3) Интервальная оценка среднего
По таблице процентных точек t – распределения Стьюдента, представленной в приложении Б, находится значение  для числа степеней свободы
для числа степеней свободы  и уровня значимости
и уровня значимости  .
.

По формуле (11) рассчитывается полуширину 95% - ого доверительного интервала  . Определяется нижняя
. Определяется нижняя  и верхняя
и верхняя  доверительная граница для математического ожидания.
доверительная граница для математического ожидания.
Рассчитанные значения представлены в таблице 1.
Таблица 1 – Результаты расчетов
| Сумма | 2085,50 |
| Сумма квадратов | 44556,25 |
| Среднее | 21,28 |
| Дисперсия | 1,81 |
| Стандартное отклонение | 1,35 |
| Медиана | 21,50 |
| Минимальное | 18,00 |
| Максимальное | 25,00 |
| Полуширина доверительного интервала | 0,27 |
| Нижняя доверительная граница | 21,011 |
| Верхняя доверительная граница | 21,550 |
4) Построение гистограммы распределения выборки
Определяется ориентировочная длина интервала разбиения по формуле:


За начало первого интервала  принимается величина меньше, чем
принимается величина меньше, чем  , т.е.
, т.е.  . Далее рассчитываются границы интервалов
. Далее рассчитываются границы интервалов  (приложение А столбец 1) до тех пор пока последнее значение
(приложение А столбец 1) до тех пор пока последнее значение  не превзойдет максимальное значение выборки.
не превзойдет максимальное значение выборки.
Подсчитываем число 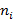 значений выборки, попавших в каждый интервал
значений выборки, попавших в каждый интервал  (приложение А столбец 2). Значение, равное границе интервалов относить к левому интервалу – интервалу с меньшим номером.
(приложение А столбец 2). Значение, равное границе интервалов относить к левому интервалу – интервалу с меньшим номером.
Построить столбчатую диаграмму, представленную на рисунке 5, где границы интервалов  откладываются по горизонтальной оси, а значения
откладываются по горизонтальной оси, а значения 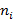 – по вертикальной.
– по вертикальной.

Рисунок 5 – Гистограмма распределения выборки
5) Построение графика проверяемого нормального распределения
Находится функция нормального распределения в точках границ интервалов  (приложение А столбец 4). Рассчитывается вероятность попадания в интервалов (приложение А столбец 5):
(приложение А столбец 4). Рассчитывается вероятность попадания в интервалов (приложение А столбец 5):

Вычисляется расчетное (теоретическое) число данных в интервале (приложение А столбец 6):

Строим кривую теоретического распределения данных по интервалам гистограммы, представленная на рисунке 6, относя каждое значение  к середине соответствующего интервала.
к середине соответствующего интервала.

Рисунок 6 - Гистограмма распределения выборки и расчетное число попаданий нормально распределенной выборки в интервалы гистограммы (линия)
С учетом требований к разбиению на интервалы для критерия Пирсона расширяется крайний левый с  на
на  и крайний правый интервал с
и крайний правый интервал с  на
на  . Новые границы интервалов представлены в приложении А столбец 7, эмпирические данные в интервале - приложение А столбец 8.
. Новые границы интервалов представлены в приложении А столбец 7, эмпирические данные в интервале - приложение А столбец 8.
Аналогично проводится расчет значение функции нормального распределения (приложение А столбец 9), вероятность попадания в интервал (приложение А столбец 10) и расчетное число данных в интервале (приложение А столбец 11) с использованием новых границ интервалов.
Рассчитывается взвешенный квадрат отклонения в интервалах  (приложение А столбец 12):
(приложение А столбец 12):

Рассчитывается величина критерия Пирсона – сумму взвешенных квадратов отклонений в интервалах по формуле:


По таблице, представленной в приложении В, определяется значение критерия Пирсона. Число степеней свободы определяется по формуле (13). Число интервалов  количество оцененных по выборке параметров распределения
количество оцененных по выборке параметров распределения  .
.

Проводится сравнение рассчитанного значения Пирсона  с табличным значением
с табличным значением 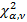 .
.

Вывод: гипотеза нормального распределения не противоречит наблюдениям с вероятностью  .
.
 2020-08-05
2020-08-05 228
228













