Основы математической статистики: динамические и статические случайные величины, и их характеристики (мода, медиана, математическое ожидание, дисперсия). Статистические гипотезы: методы доказательства основных гипотез.
Случайные характеристики (шумы):
1. Дискретные – выражаются числом. Независимые – выражаются функцией распределения.
2. Зависимые – вероятность зависит от какого-либо объятия(?). Независимые – не зависят ни от чего.
3. Белый шум – распределены по всему диапазону одинаково. Красный шум – распределение смещено вправо. Синий шум – распределение смещено влево.
Характеристики шумов:
1. Мода – наиболее часто встречаемое значение. Пример:
2 1 8 2 6 8 – в данном ряду модой являются числа 2 и 8.
2. Медиана – средняя при расположении в ряд по возрастанию или убыванию величина. Пример:
1 2 2 6 8 8 – в данном ряду медиана 4 (1 2 2 6 8 8 à 2 и 6 дают медиану 4).
3. Математическое ожидание – средневзвешенное значение случайной величины:
M(x) = Σxipi =  Σxi = xср.
Σxi = xср.
M(x) = 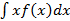
Свойства математического ожидания:
3.1. Математическое ожидание от постоянной равно самой постоянной:
M(с) = с
3.2. Постоянный множитель можно внести за скобки:
M(cx) = cM(x)
3.3. Математическое ожидание суммы равно сумме математических ожиданий:
M(x+y) = M(x) + M(y)
3.4. Математическое ожидание произведения 2 независимых случайных величин равно произведению их математических ожиданий:
M(xy) = M(x) * M(y)
4. Центральный момент случайной величины:
mn(x) = M(x-M(x))n = M(x-M(x))n
1-го порядка: m(x) = M(x-M(x))n = M(x) – M(M(x)) = 0
2-го порядка: m2(x) = M(x-M(x))2 = 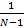 Σ(xi-xср.)2 = D(x) – дисперсия
Σ(xi-xср.)2 = D(x) – дисперсия
3-го порядка: m3(x) = M(x – M(x))3 = 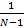 Σ(xi-xср.)3 – коэффициент ассиметрии
Σ(xi-xср.)3 – коэффициент ассиметрии
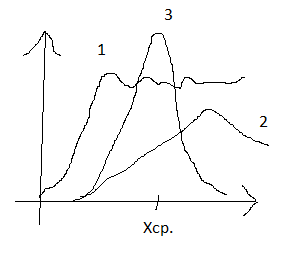
1. m3(x) > 0 2. m3(x) > 0 3. m3(x) = 0
4-го порядка: m4(x) = M(x-M(x))4 = 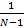 Σ(xi-xср.)4 – коэффициент эксцесса
Σ(xi-xср.)4 – коэффициент эксцесса
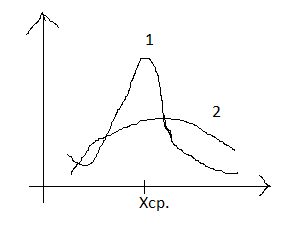
1. m4(x) = 0 2. m4(x) < 0 3. m4(x) > 0 m4(x)1 > m4(x)2
5. Свойства дисперсии D(x):
5.1. D(c) = 0
5.2. D(cx) = |cx = y| = D(y) = 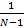 Σ(yi - yср.)2 =
Σ(yi - yср.)2 = 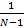 Σ(cxi - cxср.)2 = c2 *
Σ(cxi - cxср.)2 = c2 * 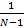 Σ(xi - xср.)2 = c2 * D(x)
Σ(xi - xср.)2 = c2 * D(x)
5.3. D(x + y) = M((x + y) - M(x + y))2 = M(x + y - M(x) - M(y))2 = M((x - M(x)) + (y – M(y))2 = M(x-M(x))2 + 2M ((x – M(x))(y – M(y)) + M(y – M(y))2 = D(x) + D(y) + cov (x,y)
(cov (x,y) – корреляционный момент (ковариация))
5.4. D(xy) ≠ D(x) * D(y)
R = 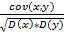 (R – коэффициент корреляции)
(R – коэффициент корреляции)
Статистическая гипотеза – любое предположение относительно свойств генеральной совокупности случайных величин.
Ошибки 1 рода (α) – принятие неверной гипотезы.
Ошибки 2 рода (β) – отвержение на самом деле верной гипотезы.

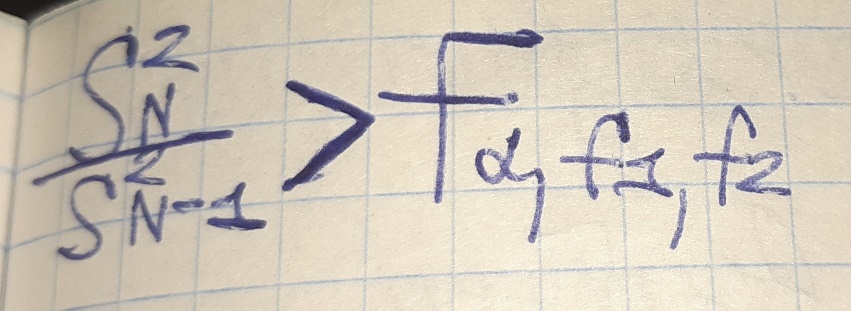
Регрессионный анализ: определение, уравнение регрессии, факторы, параметры, отклик. Метод наименьших квадратов. Решение уравнения МНК в матричной форме.
Регрессионный анализ – статистический метод исследования или влияния от одной или нескольких зависимых переменных на зависимую переменную.
Уравнение регрессии представляет собой бесконечный ряд:
y = a0 + a1x1 + a2x21 + a3x1x2 + …
(y – отклик (зависимая переменная), x – факторы, a – параметры регрессии)
Поиск линии регрессии осуществляется с использованием метода наименьших квадратов, когда минимизируется остаточная сумма квадратов (S):
S = 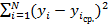 (N – объём выборки, yi – экспериментальное значение отклика, yi ср. – расчётное значение).
(N – объём выборки, yi – экспериментальное значение отклика, yi ср. – расчётное значение).
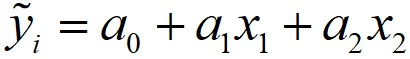
Если S → min, то:
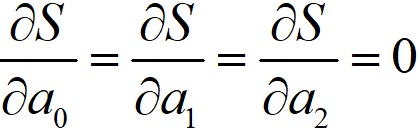
Параметру a0 добавим фактор x0, равный во всех случаях 1:
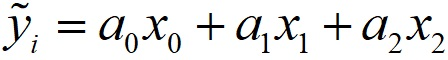
Дифференцируем остаточную сумму квадратов по a0:
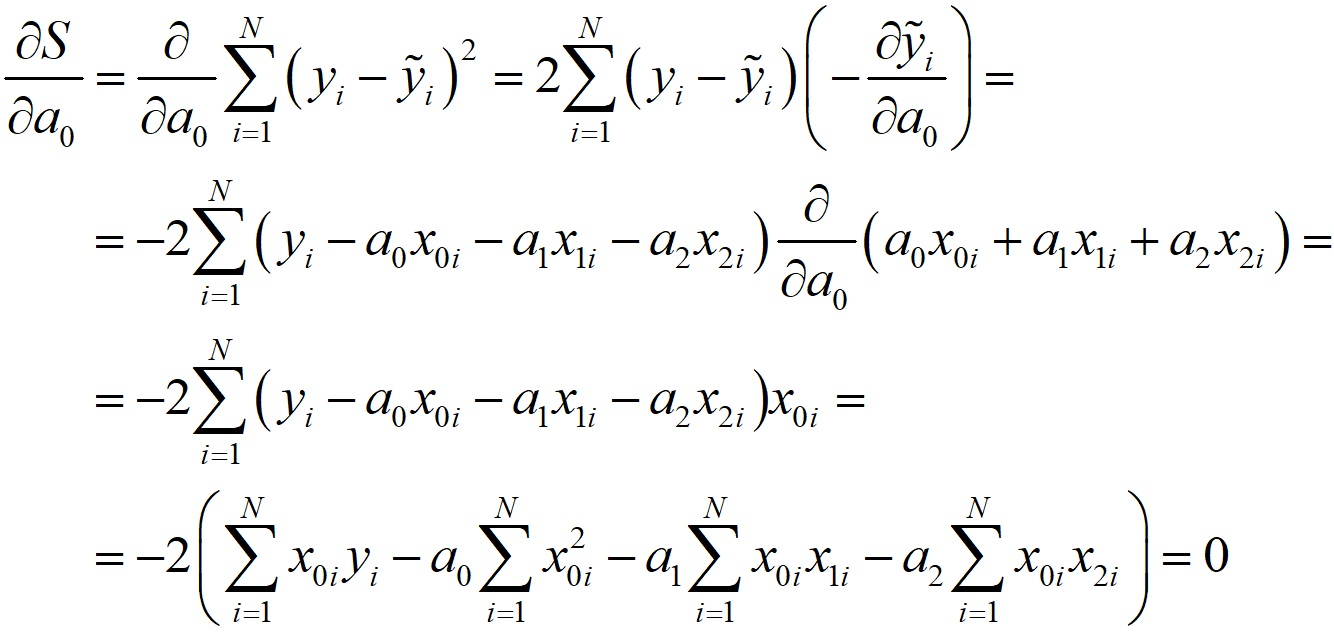
Разделяем переменные:
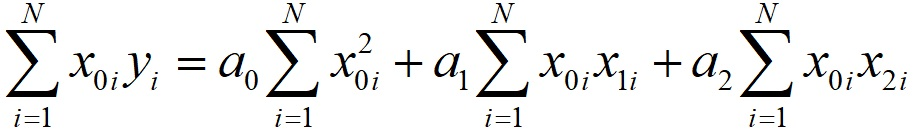
Дифференцируя аналогичным образом S по a1 и a2, получаем:
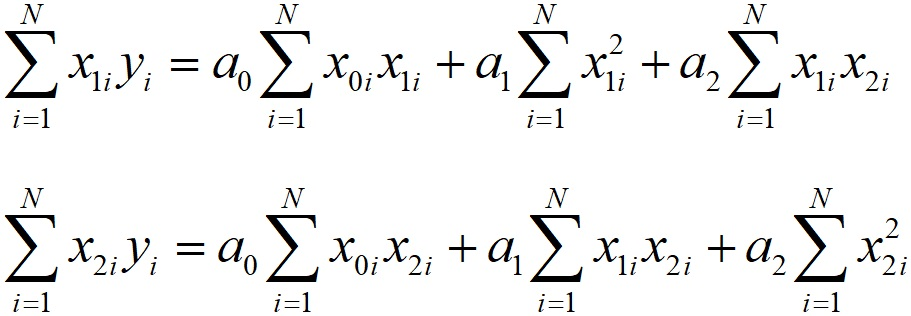
В итоге получаем три уравнения с тремя неизвестными коэффициентами регрессии. Данную систему уравнений удобнее решать в матричном виде. Для этого введём матрицу X, представляющую собой вектор-строку:
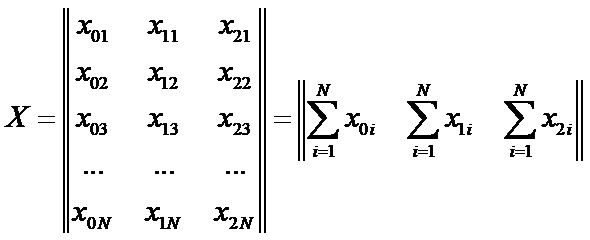
И матрицу, представляющую собой транспонированную матрицу X:
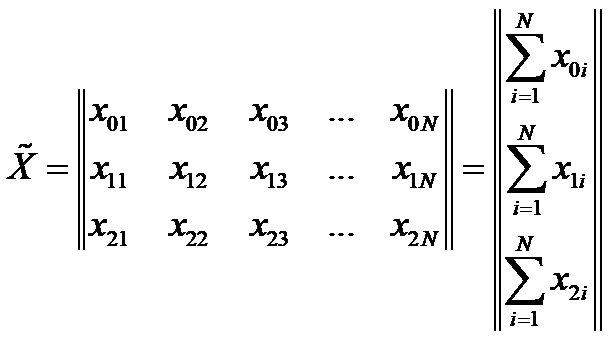
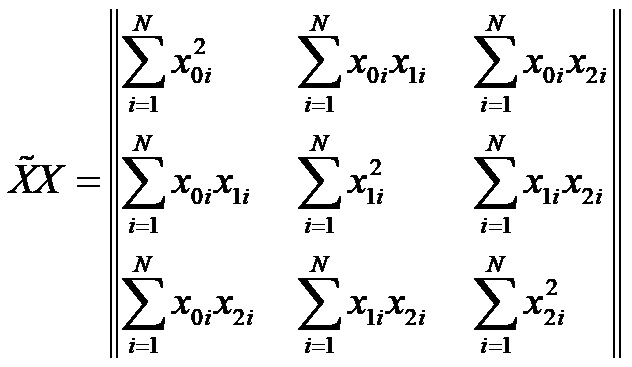
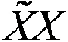 – матрица, похожая на правую часть полученной системы уравнений. Такую матрицу называют информационной.
– матрица, похожая на правую часть полученной системы уравнений. Такую матрицу называют информационной.
Чтобы в информационной матрице появились коэффициенты a, умножим её на вектор-столбец A:
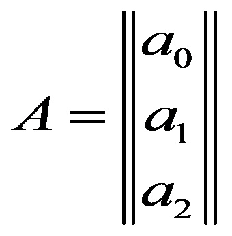
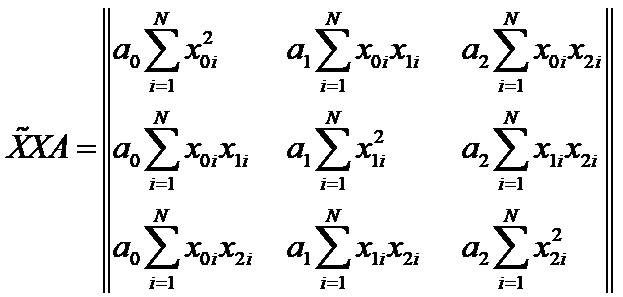
Чтобы получить левую часть системы уравнений, вводим матрицу Y, содержащую значения откликов:
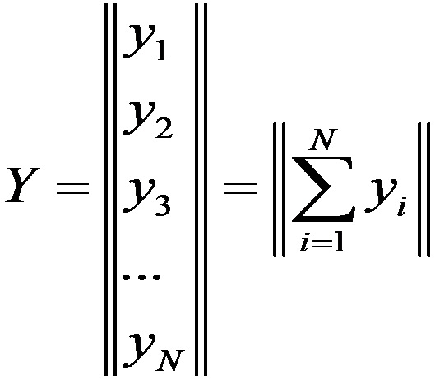
Тогда:
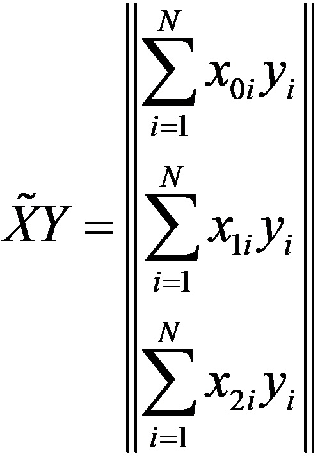
Отсюда получим основное уравнение метода наименьших квадратов для системы из N факторов:
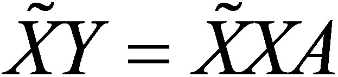
Выразим из него искомую матрицу параметров:
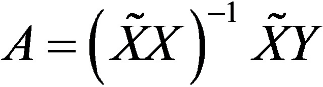
 2020-08-05
2020-08-05 203
203







