Методы нахождения оптимальных параметров модели

При определении оптимального набора параметров модели SARIMAX нужно знать как проводить оптимизацию и по какой величине. Правильная параметризация этих моделей является тщательной работой, требующей знаний по дисциплине и много времени. Для этого в программные пакеты и языки программирования для статистики (такие R) вводят автоматизированные способы поиска параметров, но на Python они не были портированы, поэтому эти способы необходимо разработать.

 

(P,D,Q) и (p,d,q)– целые неотрицательные числа, значит есть возможность генерировать тройки чисел внутри определенного интервала чисел (учитывая, что интервал не должен быть большим, чтобы не вызвать комбинаторный взрыв).

# Определить p,d,q в интервале как числа [0,2)

MAX_PDQ = 2

p = d = q = range(0, MAX_PDQ)

 

# Сгенерировать все тройки (p,d,q)

pdq = list(itertools.product(p, d, q))

 

# Точно также сгенерировать сезонные (P,D,Q)

seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]

        

    В результате полученные тройки параметров позволяют автоматизировать процесс обучения и оценки ARIMA-моделей на разных комбинациях. Такой процесс с статистике и машинном обучении называют оптимизацией гиперпараметров.

    Для  определения оценки и сравнения статистических моделей с разными параметрами модели разделим модели по признаку соответствия данным или возможности получать конкретные прогнозы. Для оценки моделей используют способ Akaike Information Criterion (AIC).

       AIC - это метод оценки относительного качества статистических моделей для набора данных. AIC используется на совокупности методов, оценивает каждую модель относительно других и позволяет определить наиболее оптимальную модель. AIC основан на теории информации и оценивает относительную потерю информации, когда модель описывает процесс, который сгенерировал набор данных. Следовательно, оптимальная модель будет иметь минимальное значение AIC.

AIC не может дать абсолютную оценку модели, поэтому, если все коллекции плохо подходят, AIC не будет указывать это. Тем не менее, AIC прост в использовании, поэтому служит полезным инструментом оценки [4].

Вычисляется AIC так:

 

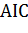=2 k – 2In ( )

 

где k – число оцениваемых параметров,

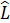 - максимальное значение функции правдоподобия.

       Вывод: AIC не только повышает вероятность (журнал максимального правдоподобия со знаком минус), но также штрафует за большое количество параметров (2k). Получается из двух моделей, которые имеют одно и тоже количество входов, более низкую AIC будет иметь та, которая имеет больший показатель максимального правдоподобия, однако, если две модели имеют одинаковый наибольший балл, то у меньшего AIC будет модель с наименьшим количеством параметров.