Смотрим в таблицу на правило (№5) дифференцирования сложной функции:
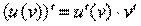
Разбираемся. Прежде всего, обратим внимание на запись 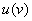 . Здесь у нас две функции –
. Здесь у нас две функции – 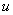 и
и 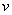 , причем функция
, причем функция 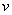 , образно говоря, вложена в функцию
, образно говоря, вложена в функцию 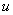 . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
. Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию 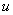 я буду называть внешней функцией, а функцию
я буду называть внешней функцией, а функцию 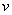 – внутренней (или вложенной) функцией.
– внутренней (или вложенной) функцией.
Для того, чтобы прояснить ситуацию, рассмотрим:
Пример 1
Найти производную функции 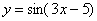
Под синусом у нас находится не просто буква «икс», а целое выражение 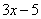 , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
, поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
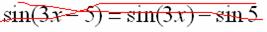
Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.
В данном примере уже из моих объяснений интуитивно понятно, что функция 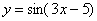 – это сложная функция, причем многочлен
– это сложная функция, причем многочлен 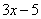 является внутренней функцией (вложением), а
является внутренней функцией (вложением), а 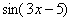 – внешней функцией.
– внешней функцией.
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции 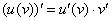 .
.
Начинаем решать. Оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:
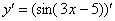
Сначала находим производную внешней функции 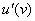 (синуса), смотрим на таблицу производных элементарных функций и замечаем, что
(синуса), смотрим на таблицу производных элементарных функций и замечаем, что 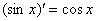 . Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:
. Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:
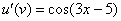
Обратите внимание, что внутренняя функция 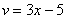 не изменилась, её мы не трогаем.
не изменилась, её мы не трогаем.
Ну и совершенно очевидно, что 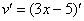
Результат применения формулы 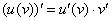 в чистовом оформлении выглядит так:
в чистовом оформлении выглядит так:
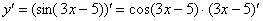
Далее мы берем производную внутренней функции, она очень простая:
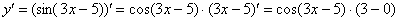
Постоянный множитель обычно выносят в начало выражения. Вот полное решение:
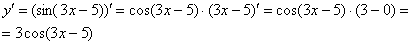
Пример 2
Найти производную функции 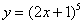
Как всегда записываем:
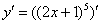
Разбираемся, где у нас внешняя функция, а где внутренняя. Многочлен 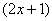 – и есть внутренняя функция:
– и есть внутренняя функция:
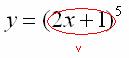
И, следовательно, степенная функция – это внешняя функция:

Согласно формуле 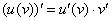 , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу:
, сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: 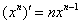 . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения. Таким образом, результат применения правила дифференцирования сложной функции
. Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения. Таким образом, результат применения правила дифференцирования сложной функции 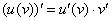 следующий:
следующий:
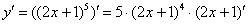
Снова подчеркиваю, что когда мы берем производную от внешней функции 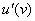 , внутренняя функция
, внутренняя функция 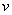 у нас не меняется:
у нас не меняется:
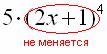
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат. Итоговая запись решения:
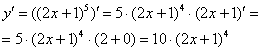
Задания для самостоятельного решения:
Найти производную функции:
2) у = 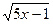 .
.
3) 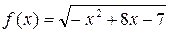
4) y = 6 3х-5;
5) f(x) = (2x-1)3
6) y = 6 ln(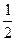 x);
x);
Надеюсь, что все понятно.
 2020-08-05
2020-08-05 161
161







