Лабораторная работа № 1-7

 

Определение момента инерции баллистического маятника и скорости полета "пули".

 

Цель работы: ознакомление с законами динамики вращательного движения.      

ВВЕДЕНИЕ

При отклонении физического маятника на небольшой угол можно считать его колебания гармоническими, и тогда период этих колебаний определяется по формуле:

 

,                                       (1)

где  - момент инерции маятника; с – коэффициента возвращающего момента, который зависит от материала, проволоки и её размеров. Из уравнения (1) следует:

 .                                             (2)

Так как коэффициент возвращающего момента трудно рассчитать, его необходимо исключить из расчетной формулы. Для этого на маятнике имеется два добавочных груза, которые могут передвигаться вдоль него. Тогда момент инерции маятника с грузами

                   ,                                             (3)

где  - момент инерции добавочного груза.

По теореме Штейнера:

                      ,                                       (4)

где - момент инерции груза (диска) относи­тельно оси,    проходящей через его центр тяжести перпендикулярно оси груза;

 - расстояние между центром тяжести груза и осью подвеса;  - масса груза (диска);  - радиус диска;  - толщина диска.

Измерив периоды колебаний маятника с грузами при двух разных их положениях, имеем:

 .                          (5)

 

             .                               (6)

Решая совместно (5) и (6), получаем

 

.

или

.                (7)

Это уравнение для определения момента инерции маятника.

Для определения скорости полета "пули" используется за­кон сохранения момента импульса. "Пуля" выстреливается в маят­ник и, застревая в нем, вызывает его отклонение. Время соуда­рения ''пули" с маятником незначительно по сравнению с перио­дом колебаний. Отклонение маятника от положения равновесия в момент соударения мало. Результирующий момент внешних сил, действующих на систему в момент удара, равен нулю. Систему маятник - "пуля" можно считать замкнутой.

Считая удар абсолютно неупругим, применим закон сохранения момента импульса: момент импульса "пули" до удара    равен моменту импульса системы "маятник - пуля" после удара:

                                

                                       ,                                     (8)

где - масса "пули"';  - момент инерции маятника с грузами без "пули" (мо­ментом инерции "пули" пренебрегаем); 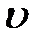- скорость "пули" в момент удара; 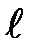- расстояние от оси маятника до центра "пули", попав­шей в маятник;  - угловая скорость системы после удара.

    Угловую скорость системы после удара можно определить из закона сохранения энергии. Максимальная кинетическая энергия колеблющегося маятника, которую он имеет, проходя положения рав­новесия, должна быть равна его максимальной потенциальной энергии , которую он имеет в положении максимального отклонения от равновесия:

                           ,                                   (9)

где  - максимальный угол отклонения маятника.

Подставляя уравнение (9) в (8) и решая его относительно 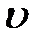, имеем

 .                                                  (10)

Коэффициент возвращающего момента

                                        .                                        (11)                                                     

Тогда окончательно получим

 

                     .                                (12)                    

Для нахождения момента инерции маятника   графически можно построить график , зная периоды колебаний маятника минимум при трех положениях добавочных грузов. График должен представлять собой прямую, уравнение которой имеет вид:

 

.               (13)

A

O

Рис. 1

 

На рис.1 отрезок ОА равен второму слагаемому в уравнении (13):

 

 .                  (14)

Множитель  равен тангенсу угла наклона прямой к оси абсцисс:

.                                      (15)

Таким образом, используя формулу (14) и график (рис.1), можно найти :

.                          (16)