Теорема Ферма
Теорема Ферма [1]
Если функция f (x) определена в некотором промежутке, во внутренней точке этого промежутка принимает наибольшее или наименьшее значение и имеет в этой точке производную 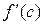 , то эта производная равна нулю
, то эта производная равна нулю 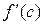 = 0.
= 0.
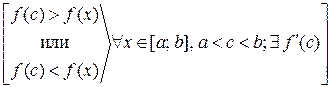 Þ
Þ 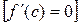 .
.
Дано: 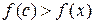 ,
, 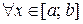 ,
, 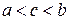 ,
,
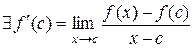 .
.
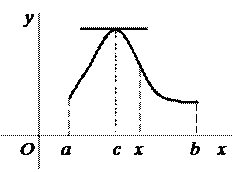 Доказать:
Доказать: 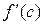 = 0.
= 0.
Доказательство:
т.к. f (c)> f (x), 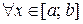 Þ
Þ 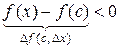 для
для 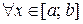 (рис. 1),
(рис. 1), 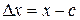 , Рис. 1
, Рис. 1
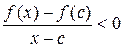 , если
, если 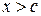 и
и 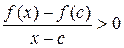 , если
, если 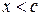 .
.
Перейдем в неравенствах к пределу.
Знак неравенства при переходе к пределу ослабевает.
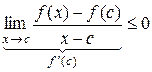 , если
, если 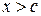 и
и 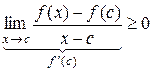 , если
, если 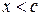 .
.
Получаем неравенство: 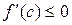 и
и 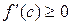 , следовательно
, следовательно 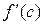 = 0.
= 0.
Теорема Ролля, Лагранжа и Коши.
Теорема Ролля [2]
Если функция f (x) непрерывна на отрезке [ a; b ], дифференцируема внутри него и f (a) = f (b), то внутри промежутка [ a; b ] найдется хотя бы одна точка x = c, в которой производная данной функции равна 0.
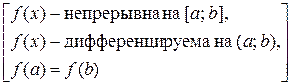 Þ
Þ 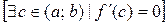
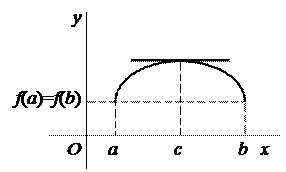
Рис. 2.
Доказательство:
По свойству функций, непрерывных на отрезке, функция 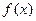 на отрезке [ a; b ] принимает наибольшее и наименьшее значения, которые обозначим соответственно
на отрезке [ a; b ] принимает наибольшее и наименьшее значения, которые обозначим соответственно 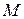 и
и 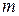 . Имеются две возможности: или
. Имеются две возможности: или 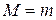 , или
, или 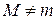 . Рассмотрим их.
. Рассмотрим их.
Пусть 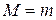 . Тогда функция
. Тогда функция 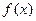 на отрезке [ a; b ] сохраняет постоянное значение и, следовательно, в любой точке интервала (a; b) ее производная равна нулю. В этом случае за с можно взять любую точку интервала (a; b).
на отрезке [ a; b ] сохраняет постоянное значение и, следовательно, в любой точке интервала (a; b) ее производная равна нулю. В этом случае за с можно взять любую точку интервала (a; b).
Пусть 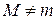 . Так как значения функции на концах отрезка равны, то хотя бы одно из значений
. Так как значения функции на концах отрезка равны, то хотя бы одно из значений 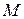 или
или 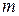 функция принимает внутри отрезка
функция принимает внутри отрезка
[ a; b ]. Обозначим f (с) = M, 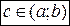 , так как
, так как 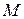 - наибольшее значение функции, то для всех
- наибольшее значение функции, то для всех 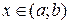 выполняется неравенство
выполняется неравенство 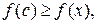 Найдем производную
Найдем производную 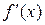 в точке
в точке 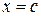 ,
, 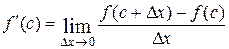 .
.
Выполняется неравенство 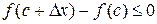 , так как
, так как 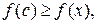
Если 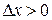 (т.е.
(т.е. 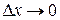 справа от точки
справа от точки 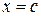 ), то
), то 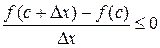 и поэтому
и поэтому 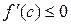 . Если
. Если 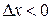 (т.е.
(т.е. 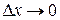 слева от точки
слева от точки 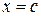 ), то
), то 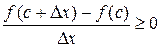 и
и 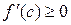 . Следовательно, получаем
. Следовательно, получаем 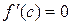 .
.
В случае 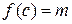 , доказательство аналогичное.
, доказательство аналогичное.
Геометрический смысл теоремы Ролля:
Если условия теоремы выполняются, то на интервале (a; b) существует такая точка c, что в соответствующей точке кривой 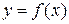 касательная параллельна оси
касательная параллельна оси 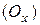 . (Рис.2)
. (Рис.2)
Физическая интерпретация теоремы Ролля.
Пусть 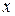 - время, а
- время, а 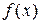 - координата точки, движущейся по прямой, в момент времени
- координата точки, движущейся по прямой, в момент времени 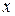 . В начальный момент
. В начальный момент 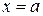 точка имеет координату
точка имеет координату 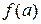 , далее движется определенным образом со скоростью
, далее движется определенным образом со скоростью 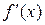 и в момент времени
и в момент времени 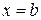 она возвращается в точку с координатой
она возвращается в точку с координатой 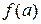 , т.е.
, т.е. 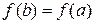 . Ясно, что для возвращения в точку
. Ясно, что для возвращения в точку 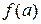 она должна остановиться в некоторый момент времени (прежде чем «повернуть назад»), т.е. в некоторый момент
она должна остановиться в некоторый момент времени (прежде чем «повернуть назад»), т.е. в некоторый момент 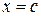 скорость
скорость 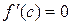 .
.
Пример. Проверим, применима ли теорема Ролля к функции 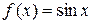 на отрезке
на отрезке 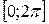 . Если окажется, что теорема применима, то найдем точку
. Если окажется, что теорема применима, то найдем точку 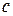 , в которой производная данной функции равна нулю.
, в которой производная данной функции равна нулю.
Решение:
Функция 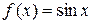 непрерывна на отрезке
непрерывна на отрезке 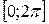 , ее производная
, ее производная 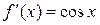 определена всюду на интервале
определена всюду на интервале 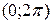 , выполняется условие
, выполняется условие 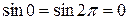 . Значит, все три условия теоремы Ролля выполнены. В качестве точки
. Значит, все три условия теоремы Ролля выполнены. В качестве точки 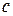 можно выбрать
можно выбрать 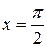 , так как
, так как 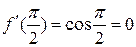 . Заметим, что можно было положить
. Заметим, что можно было положить 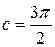 .
.
Ответ: 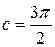
Пример. Покажем, что уравнение 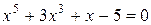 имеет только один действительный корень.
имеет только один действительный корень.
Решение:
Рассмотрим функцию 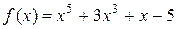 . Она непрерывна и дифференцируема на всей числовой прямой, причем
. Она непрерывна и дифференцируема на всей числовой прямой, причем 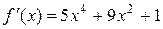 .
.
Можно заметить, что при любом значении 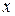 имеем
имеем 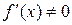 . Но тогда уравнение может иметь не более одного действительного корня. В самом деле, если бы оно имело два корня
. Но тогда уравнение может иметь не более одного действительного корня. В самом деле, если бы оно имело два корня 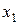 и
и 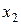 (
(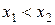 ), то, применив к функции
), то, применив к функции 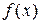 на отрезке
на отрезке 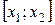 теорему Ролля, убедились что все условия теоремы Ролля здесь выполнены:
теорему Ролля, убедились что все условия теоремы Ролля здесь выполнены: 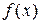 непрерывна на отрезке
непрерывна на отрезке 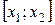 , дифференцируема на интервале
, дифференцируема на интервале 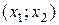 и
и 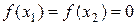 , получили бы, что между
, получили бы, что между 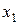 и
и 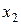 существует точка
существует точка 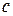 такая, что
такая, что 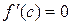 . Последнее невозможно, значит, уравнение имеет не более одного действительного корня. Существование действительного корня следует из того, что
. Последнее невозможно, значит, уравнение имеет не более одного действительного корня. Существование действительного корня следует из того, что 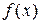 -многочлен нечетной степени (корень
-многочлен нечетной степени (корень 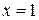 в данном случае легко найти подбором).
в данном случае легко найти подбором).
Пример. Дана функция 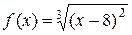 . Пусть
. Пусть 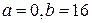 . Тогда
. Тогда 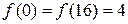 . Однако производная
. Однако производная 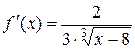 не обращается в нуль ни в одной точке интервала
не обращается в нуль ни в одной точке интервала 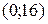 . Противоречит ли это теореме Ролля?
. Противоречит ли это теореме Ролля?
Решение:
Нет, не противоречит,т.к. в точке 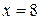 интервала
интервала 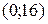 производная не существует, и условия теоремы нарушены.
производная не существует, и условия теоремы нарушены.
Теорема Лагранжа [3]
Если функция f (x) непрерывна на отрезке [ a; b ] и дифференцируема внутри него, то существует хотя бы одна точка внутри промежутка [ a; b ] такая, в которой выполняется соотношение:
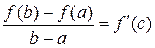
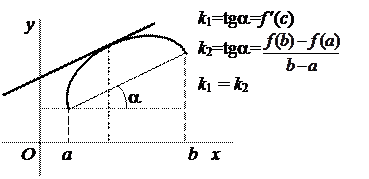 |
Рис. 3
Доказательство:
Рассмотрим вспомогательную функцию
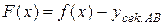 . Уравнение секущей
. Уравнение секущей 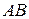 (по точке
(по точке 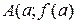 и угловому коэффициенту) имеет вид:
и угловому коэффициенту) имеет вид: 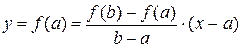 , при этом
, при этом 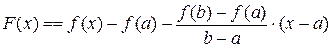 . Функция
. Функция 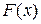 удовлетворяет условиям теоремы Ролля. Действительно, она непрерывна на отрезке
удовлетворяет условиям теоремы Ролля. Действительно, она непрерывна на отрезке 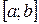 и дифференцируема на интервале
и дифференцируема на интервале 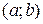 . Подставляя
. Подставляя 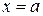 и
и
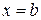 в функцию
в функцию 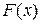 нетрудно проверить что
нетрудно проверить что 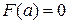 и
и 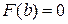 , т.е.
, т.е. 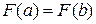 . По теореме Ролля существует по крайней мере одна такая точка
. По теореме Ролля существует по крайней мере одна такая точка 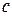 ,
, 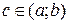 , что
, что 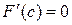 . Так как
. Так как 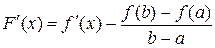 , то, следовательно,
, то, следовательно, 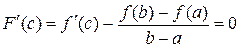 . Откуда получаем:
. Откуда получаем: 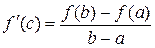 , что и требовалось доказать.
, что и требовалось доказать.
Равенство 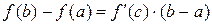 , где
, где 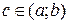 называется формулой Лагранжа, или формулой конечных приращений.
называется формулой Лагранжа, или формулой конечных приращений.
Замечание.
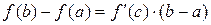 или
или 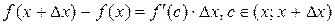 –
–
формула Лагранжа (конечных приращений).
Геометрический смысл теоремы Лагранжа.
Отношение 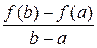 равно угловому коэффициенту секущей
равно угловому коэффициенту секущей 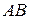 (Рис.3).
(Рис.3).
Если функция 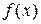 удовлетворяет условиям теоремы, то на интервале
удовлетворяет условиям теоремы, то на интервале 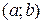 существует точка
существует точка 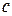 , такая, что в соответствующей точке кривой
, такая, что в соответствующей точке кривой 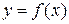 касательная параллельна секущей, соединяющей точки
касательная параллельна секущей, соединяющей точки 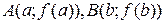 . Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.
. Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.
Физическая интерпретация теоремы Лагранжа.
Пусть 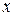 - время,
- время, 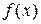 - координата точки, движущейся по прямой, в
- координата точки, движущейся по прямой, в
момент времени 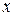 . Запишем формулу Лагранжа в виде
. Запишем формулу Лагранжа в виде 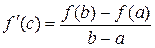 . Величина в правой части является средней скоростью
. Величина в правой части является средней скоростью
движения точки по прямой за промежуток времени от 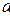 до
до 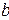 . Формула Лагранжа показывает, что существует такой момент времени
. Формула Лагранжа показывает, что существует такой момент времени 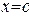 , в который мгновенная скорость равна средней скорости на временном отрезке
, в который мгновенная скорость равна средней скорости на временном отрезке 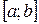 .
.
Cледствие. Если функция 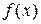 непрерывна на отрезке
непрерывна на отрезке 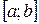 и во всех
и во всех
внутренних точках отрезка ее производная равна нулю, то функция 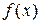
постоянна на этом отрезке.
Доказательство:
Пусть 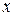 - точка из промежутка
- точка из промежутка 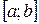 . Тогда по теореме
. Тогда по теореме
Лагранжа 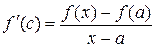 , где
, где 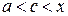 . Но по условию
. Но по условию 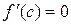 ,
,
следовательно, 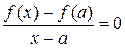 , откуда
, откуда 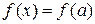 . Это и означает, что
. Это и означает, что
рассматриваемая функция постоянна на данном отрезке.
Доказанное утверждение имеет простой физический смысл: если скорость
точки все время равна нулю, то точка покоится и ее координата не
меняется (постоянна).
Замечании.: Если 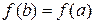 , то из равенства
, то из равенства 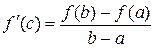 следует
следует 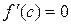 . Это значит, что теорема Ролля есть частный случай теоремы Лагранжа.
. Это значит, что теорема Ролля есть частный случай теоремы Лагранжа.
Пример. Проверим, применима ли теорема Лагранжа к функции
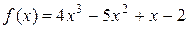 на отрезке
на отрезке 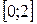 . Если окажется, что теорема
. Если окажется, что теорема
применима, то найдем точку 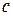 , в которой выполняется равенство
, в которой выполняется равенство 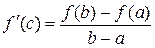 .
.
Решение:
Функция 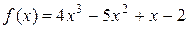 непрерывна на отрезке
непрерывна на отрезке 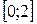 и
и
дифференцируема в интервале 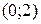 . Значит, условия теоремы Лагранжа
. Значит, условия теоремы Лагранжа
выполнены. Из формулы 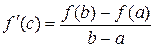 получаем:
получаем:
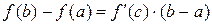 .
.
В данном случае 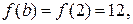
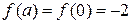 ,
, 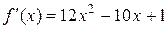 ,
, 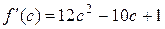 .
.
Подставим полученные значения в формулу 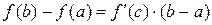 Лагранжа:
Лагранжа: 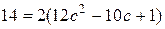 . Из этого уравнения находим
. Из этого уравнения находим 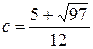 (второй корень уравнения
(второй корень уравнения 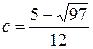 не подходит, так как это число не принадлежит отрезку
не подходит, так как это число не принадлежит отрезку 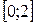 ).
).
Ответ: 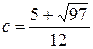
Теорема Коши [4]
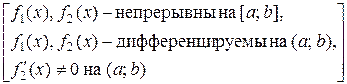 Þ
Þ
Þ 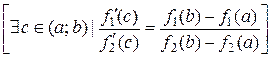 .Т.е. отношение приращений функций на данном отрезке равно отношению их производных в точке
.Т.е. отношение приращений функций на данном отрезке равно отношению их производных в точке
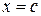 .
.
Замечание. Теорема Коши – обобщение теоремы Лагранжа, в случае
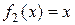 получаем теорему Лагранжа.
получаем теорему Лагранжа.
Доказательство:
Прежде чем перейти к доказательству теоремы Коши,
сначала докажем, что 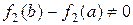 . Действительно, если допустить, что
. Действительно, если допустить, что
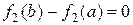 или
или 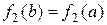 , то по теореме Ролля для функции
, то по теореме Ролля для функции 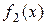
найдется точка 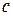 , (
, (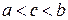 ), в которой
), в которой 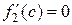 . А это противоречит
. А это противоречит
условию, т.к. 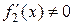 на интервале
на интервале 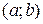 .
.
Для доказательства теоремы рассмотрим вспомогательную функцию
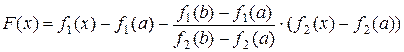 . Эта функция
. Эта функция
удовлетворяет всем условиям Ролля: непрерывна на отрезке 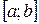 и
и
дифференцируема на интервале 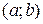 , т.к. является линейной комбинацией
, т.к. является линейной комбинацией
функций 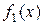 и
и 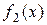 ; на концах отрезка она принимает равные значения
; на концах отрезка она принимает равные значения
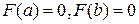 , т.е.
, т.е. 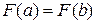 . По теореме Ролля для функции
. По теореме Ролля для функции
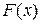 существует точка
существует точка 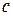 , (
, (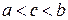 ), такая, что
), такая, что 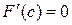 . Так как
. Так как
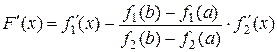 , то
, то 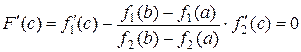 .
.
Отсюда, учитывая, что 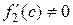 , получаем:
, получаем: 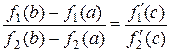 , что и
, что и
требовалось доказать.
Пример. Пусть 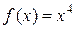 ,
, 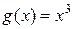 ,
, 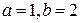 . Составим формулу Коши и
. Составим формулу Коши и
найдем значение 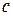 .
.
Решение:
Функции 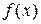 и
и 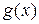 непрерывны на отрезке
непрерывны на отрезке 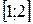 ,
,
дифференцируемы в интервале 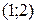 и
и 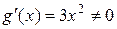 в интервале
в интервале 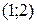 .
.
Следовательно, условия теоремы Коши выполнены и, значит, существует
точка 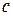 такая, что
такая, что 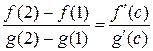 . Найдем эту точку. Имеем:
. Найдем эту точку. Имеем:
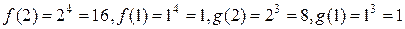 ,
,
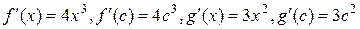 . Значит,
. Значит, 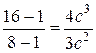 . Из этого
. Из этого
уравнения находим 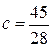 .
.
Ответ: 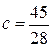
Теорема Лопиталя
До сих пор при вычислении пределов функций применяли разнообразные приемы, зачастую весьма искусственные. Теорема Лопиталя определяет простой и единообразный метод вычисления пределов различных функций. Рассмотрим способ раскрытия неопределенностей вида 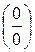 и
и 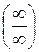 , который основан на применении производных.
, который основан на применении производных.
Теорема Лопиталя [5]
Пусть 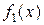 и
и 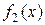 – бесконечно малые при x ® a функции,
– бесконечно малые при x ® a функции, 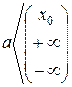 , т.е.
, т.е. 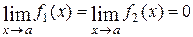 . Если функции
. Если функции 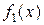 и
и 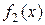 непрерывны в точке
непрерывны в точке 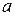 , дифференцируемы в некоторой окрестности точки а (за исключением быть может самой точки а) и
, дифференцируемы в некоторой окрестности точки а (за исключением быть может самой точки а) и 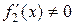 при
при 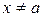 , то
, то 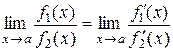 , в предположении, что предел отношения производных существует.
, в предположении, что предел отношения производных существует.
Предел отношения двух бесконечно больших (бесконечно малых)) функций равен пределу отношения их производных (если он существует)
Доказательство: Применяя формулу Коши, получим: 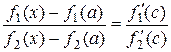 , где
, где 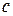 между
между 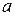 и
и 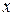 . Или, учитывая, что
. Или, учитывая, что 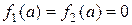 , т.к. функции
, т.к. функции 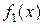 и
и 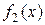 - бесконечно малые, непрерывные в точке
- бесконечно малые, непрерывные в точке 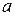 функции, получаем
функции, получаем 
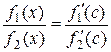 . Пусть при
. Пусть при
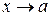 отношение
отношение 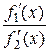 стремится к некоторому пределу. Так как
стремится к некоторому пределу. Так как 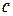 лежит между
лежит между 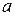 и
и 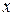 , то при
, то при 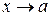 получим
получим 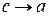 , а следовательно, и отношение
, а следовательно, и отношение 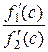 стремится к тому же пределу. Учитывая равенство
стремится к тому же пределу. Учитывая равенство 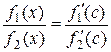 , получим: если при
, получим: если при 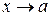 существует предел отношения
существует предел отношения 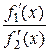 ,то
,то 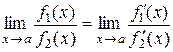 , а это и требовалось доказать. Если же окажется, что
, а это и требовалось доказать. Если же окажется, что 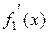 и
и 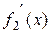 бесконечно малые при
бесконечно малые при 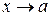 , то правило Лопиталя применяется повторно. Иногда приходится правило Лопиталя применять несколько раз.
, то правило Лопиталя применяется повторно. Иногда приходится правило Лопиталя применять несколько раз.
Пример. Вычислить предел, применяя правило Лопиталя: 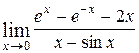
Решение: 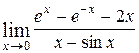 =
= 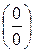 =
= 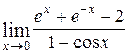 =
= 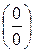 =
= 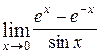 =
=  =
= 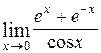 =
= 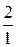 =
= 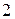
Ответ: 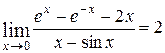 .
.
Теорема справедлива и в том случае, когда 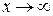 . Пусть
. Пусть 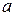 - символ
- символ 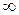 (рассуждения сохраняются и для символов
(рассуждения сохраняются и для символов 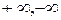 ), положив
), положив 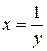 , получим, что
, получим, что 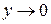 при
при 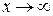 , и поэтому если существует предел отношения функций
, и поэтому если существует предел отношения функций 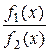 при
при 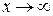 , то существует и предел отношения функций
, то существует и предел отношения функций 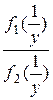 при
при 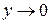 и они равны. Тоже можно сказать и об отношении их производных. Функции
и они равны. Тоже можно сказать и об отношении их производных. Функции 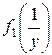 ,
, 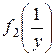 вблизи точки
вблизи точки 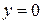 удовлетворяют условиям доказанной теоремы, поэтому на основании равенства
удовлетворяют условиям доказанной теоремы, поэтому на основании равенства 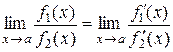 имеем:
имеем: 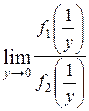 =
= 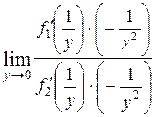 =
= 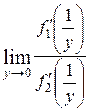 , откуда получаем:
, откуда получаем: 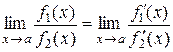 .
.
Теорема Лопиталя
Пусть 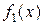 и
и 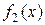 – бесконечно,большие при x ® a функции,
– бесконечно,большие при x ® a функции,  , т.е.
, т.е. 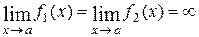 . Если функции
. Если функции 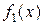 и
и 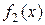 дифференцируемы в некоторой окрестности точки а (за исключением быть может самой точки а) и
дифференцируемы в некоторой окрестности точки а (за исключением быть может самой точки а) и 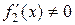 при
при 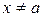 , то
, то 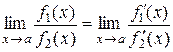 , в предположении, что предел отношения производных существует.
, в предположении, что предел отношения производных существует.
Пример 6. Вычислить 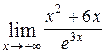
Решение: 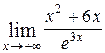 =
= 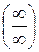 =
= 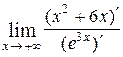 =
= 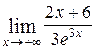 =
= 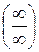 =
= 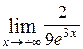 =
= 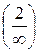 =0
=0
Ответ: 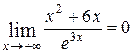 .
.
Замечания. 1) Теорему Лопиталя можно применять многократно.
2) С помощью теоремы Лопиталя раскрываются неопределенности вида: 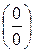 ;
; 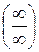 ; (0×¥); (¥-¥); (1¥); (00); (¥0).
; (0×¥); (¥-¥); (1¥); (00); (¥0).
3) Раскрытие неопределенностей вида 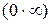 и
и 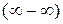 можно свести к рассмотренным выше случаям неопределенностей вида
можно свести к рассмотренным выше случаям неопределенностей вида 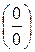 и
и 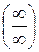 .
.
Пусть, например, 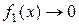 ,
, 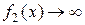 при
при 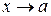 (
(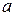 -число или один из символов:
-число или один из символов: 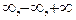 ), тогда
), тогда  неопределенность вида
неопределенность вида  , или
, или 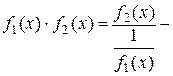 неопределенность вида
неопределенность вида 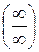 .
.
Пример 7. Вычислить 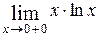
Решение: 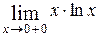 =
= 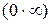 =
= 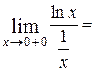
 =
= 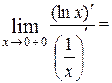
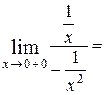
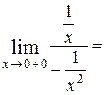
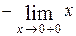 =0.
=0.
Ответ: 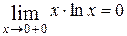
4) Неопределенности вида 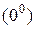 ,
, 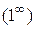 ,
, 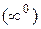 встречаются при нахождении предела функции
встречаются при нахождении предела функции 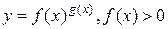 при
при 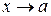 . Для нахождения предела такой функции при
. Для нахождения предела такой функции при 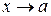 достаточно найти предел при
достаточно найти предел при 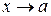 функции
функции 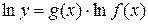 . Действительно, если
. Действительно, если 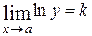 , то
, то 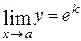 . При отыскании предела
. При отыскании предела 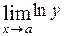 придется раскрывать неопределенность вида
придется раскрывать неопределенность вида 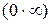 , которая приводится к виду
, которая приводится к виду 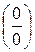 или
или 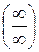 .
.
Для раскрытия неопределенности 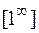 ,
, 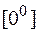 ,
, 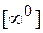 используем равенство:
используем равенство:
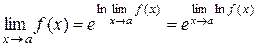 .
.
(Справедливо для непрерывной и положительной функции 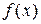 )
)
Пример 8. 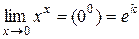
Решение:
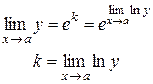
1) 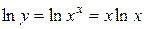 ,
,
2) 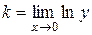 =
= 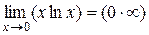 =
= 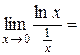
 = =
= = 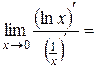
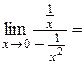
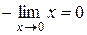 .
.
Ответ: 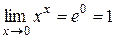 .
.
Раскрывая неопределенности по правилу Лопиталя, следует помнить и те способы раскрытия неопределенностей, с которыми знакомились в разделе «Введение в анализ». Например, во многих случаях дифференцирование, которое мы применяем по правилу Лопиталя, приводит к более простым выражениям, если предварительно заменить бесконечно малую эквивалентной ей бесконечно малой или выполнить необходимые упрощения.
Пример 9. Вычислить 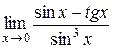
Решение: 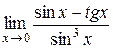 =
= 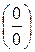
Так как 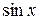 - эквивалентна
- эквивалентна 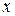 при
при 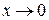 , то
, то 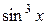 - эквивалентна
- эквивалентна 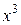 и, следовательно,
и, следовательно, 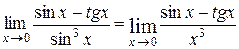 . Имеем неопределенность вида
. Имеем неопределенность вида 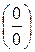 . Применив правило Лопиталя, получим:
. Применив правило Лопиталя, получим: 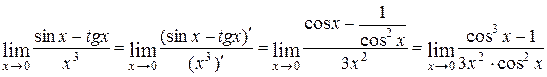
Снова имеем неопределенность вида 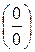 и вновь применим правило Лопиталя. Но прежде чем перейти к повторному дифференцированию,
и вновь применим правило Лопиталя. Но прежде чем перейти к повторному дифференцированию,
воспользуемся тем, что 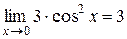 . Получим:
. Получим: 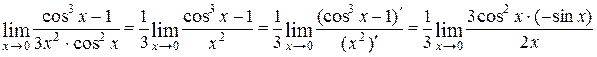 =
= 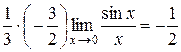
Ответ: 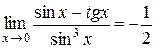
Пример 10. Вычислить 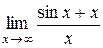
Решение: Данный предел представляет собой неопределенность вида 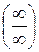 .
.
Однако правило Лопиталя не может быть к нему применено, так как предел
отношения производных, т.е. 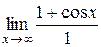 не существует. Для вычисления предела разделим числитель почленно на знаменатель:
не существует. Для вычисления предела разделим числитель почленно на знаменатель: 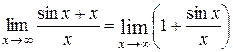 . Так как
. Так как 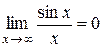 , то
, то 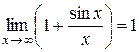
Ответ: 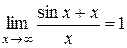
 2020-08-05
2020-08-05 6958
6958