1. Сформулируйте теорему Ролля.
2. Поясните на примерах необходимость каждого из трех условий теоремы Ролля.
3. Останется ли справедливой теорема Ролля, если не будет выполняться условие: а) 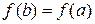 ; в)
; в) 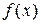 -непрерывна на
-непрерывна на 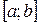 ?
?
4. Сформулируйте теорему Лагранжа. В чем состоит ее геометрический смысл?
5. Какова геометрическая интерпретация теоремы Ролля?
6. Поясните на примерах необходимость каждого из условий теоремы Лагранжа.
7.Покажите, что теорема Ролля- частный случай теоремы Лагранжа.
8. Сформулируйте условие постоянства функции, непрерывной на отрезке. В чем состоит физический смысл этой теоремы?
9. Сформулируйте теорему Коши.
10. Поясните, почему теорема Лагранжа является частным случаем теоремы Коши.
11. Поясните, почему теорема Коши не применима для функций 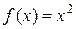 и
и 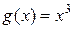 на отрезке
на отрезке 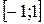 .
.
12. Сформулируйте правило Лопиталя раскрытия неопределенности вида 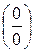 при
при 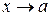 ;
; 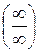 при
при 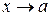 .
.
13. К раскрытию неопределенностей какого вида применимо правило Лопиталя?
Задачи к главе 2.
2.1. Выполняется ли теорема Ролля для функции 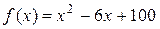 , если
, если 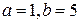 ? При каком значении
? При каком значении 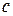 ?
?
2.1. 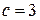
2. 2.Выполняется ли теорема Ролля для функции 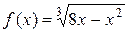 , если
, если 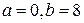 ? При каком значении
? При каком значении 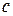 ?
?
2.2. 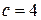
2.3. Проверить справедливость теоремы Ролля для функции 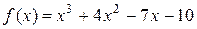 на отрезке
на отрезке 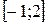 .
.
2.4. Проверить справедливость теоремы Ролля для функции  на отрезке
на отрезке 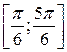 .
.
2.5. Проверить справедливость теоремы Ролля для функции 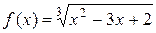 на отрезке
на отрезке 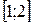 .
.
2.6. Показать, что производная многочлена 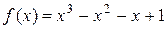 имеет действительный корень в интервале
имеет действительный корень в интервале 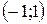 .
.
2.6. 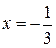
2.7.Для функции 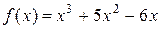 назаданном отрезке
назаданном отрезке 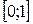 проверьте возможность применения теоремы Ролля и найдите
проверьте возможность применения теоремы Ролля и найдите 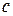 .
.
2.7. 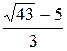
2.8. Покажите, что между корнями функции 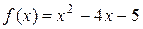 находится один корень ее производной, и найдите
находится один корень ее производной, и найдите 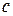 (
(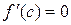 ). Приведите графическую иллюстрацию.
). Приведите графическую иллюстрацию.
2.8. 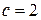
2.9. Для функции 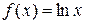 на заданном отрезке
на заданном отрезке 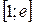 проверьте возможность применения теоремы Лагранжа; найдите
проверьте возможность применения теоремы Лагранжа; найдите 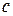 в формуле Лагранжа.
в формуле Лагранжа.
2.9. 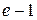
2.10. Не находя производной функции 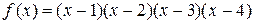 , выяснить, сколько действительных корней имеет уравнение
, выяснить, сколько действительных корней имеет уравнение 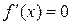 , и указать интервалы, в которых они лежат.
, и указать интервалы, в которых они лежат.
2.10. Три корня, принадлежащие соответственно интервалам 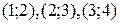
2.11. В какой точке М кривой 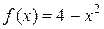 касательная параллельна хорде, проходящей через точки
касательная параллельна хорде, проходящей через точки 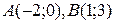 ?
?
2.11. 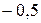
2.12. На дуге 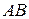 кривой
кривой 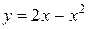 найти точку
найти точку  , в которой касательная параллельна хорде
, в которой касательная параллельна хорде 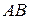 , если
, если 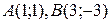 .
.
2.12. 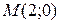
2.13. Написать формулу Лагранжа для функции 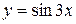 на отрезке
на отрезке 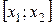 .
.
2.14. Написать формулу Лагранжа для функции 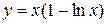 на отрезке
на отрезке 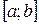 .
.
2.15. Функция 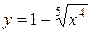 обращается в нуль на концах отрезка
обращается в нуль на концах отрезка 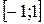 . Убедиться в том, что производная этой функции нигде в интервале
. Убедиться в том, что производная этой функции нигде в интервале 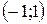 в нуль не обращается. Объяснить, почему здесь неприменима теорема Ролля.
в нуль не обращается. Объяснить, почему здесь неприменима теорема Ролля.
2.16. Доказать, что 
2.17. Используя формулу Лагранжа, докажите справедливость неравенств:
а) 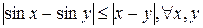
б) 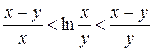
2.18. Справедлива ли формула Коши для функций 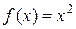 и
и 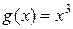 на отрезке
на отрезке 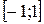 ? Какое условие теоремы Коши не выполнено для этих функций?
? Какое условие теоремы Коши не выполнено для этих функций?
2.19. Написать формулу Коши для функций 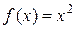 ,
, 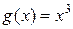 на отрезке
на отрезке 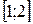 и найти
и найти 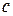 .
.
2.19. 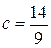
2.20. Определите значение 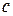 в формуле Коши для функций
в формуле Коши для функций 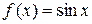 и
и 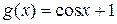 на отрезке
на отрезке 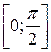 .
.
2.20. 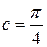
2.21. Вычислить пределы:
1) 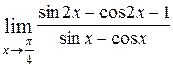 2)
2) 
3) 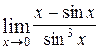 4)
4) 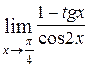
5) 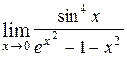 6)
6) 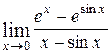
7) 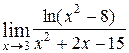 8)
8) 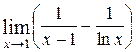
9) 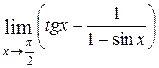 10)
10) 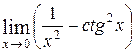
11) 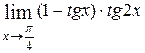 12)
12) 
13) 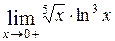 14)
14) 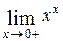
15) 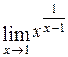 16)
16) 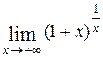
17) 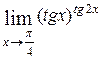 18)
18) 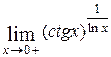
19) 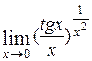 20)
20)  21)
21) 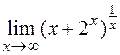 22)
22) 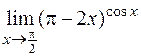
23) 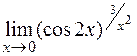 24)
24) 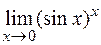 .
.
[1] Пьер Ферма (1601 – 1665), французский юрист и математик. С 1631 г. до конца жизни работал советником парламента в Тулузе, на досуге изучал математику.
[2] Мишель Ролль (1652 – 1719), французский математик, член Парижской АН. В 23 года решил одну из неопределенных задач, которую не смог решить известный в то время математик Озанам. Ролля пригласили в Парижскую АН и он до конца жизни был платным её членом.
[3] Жозеф Луи Лагранж (1736 – 1813), французский математик и механик, член Берлинской АН, ПАрижской АН, почетный член Петербургской АН. Высшее образование получил в артиллерийском училище в Турции. Еще до окончания училища начал преподавать в нем математику.
[4] Огюстен Коши (1789 – 1857), французский математик, член Парижской АН. Окончил политехническую школу, школу мостов и дорог. Работал инженером путей сообщения, затем занялся научными трудами и преподаванием
[5] Лопиталь де Гийом Фрасуа (1661 – 1704), французский математик, член Парижской АН. Изучал математику под руководством Бернулли. Издал первый печатный учебник по дифференциальному исчислению «Анализ бесконечно малых» (1696). Создал курс аналитической геометрии конических сечений.
 2020-08-05
2020-08-05 233
233







