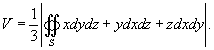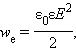Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
Важно отметить, что для того, чтобы закон был верен, необходимы:
- Точечность зарядов, то есть расстояние между заряженными телами должно быть много больше их размеров
- Их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;
- Расположение зарядов в вакууме.
В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:
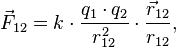
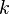 — коэффициент пропорциональности.
— коэффициент пропорциональности.
:

где 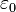 ≈ 8,854187817·10−12 Ф/м — электрическая постоянная.
≈ 8,854187817·10−12 Ф/м — электрическая постоянная.
В однородном изотропном веществе в знаменатель формулы добавляется диэлектрическая проницаемость среды ε.
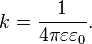
Вопрос 2:
Электрическое поле
По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.
Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не производит заметного перераспределения исследуемых зарядов.
Для количественного определения электрического поля вводится силовая характеристика  напряженность электрического поля.
напряженность электрического поля.
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда:
|
Напряженность электрического поля – векторная физическая величина. Направление вектора Е в каждой точке пространства совпадает с направлением силы, действующей на положительный пробный заряд.
напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:
|
Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции.
В соответствии с законом Кулона напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю
|
Это поле называется кулоновским. В кулоновском поле направление вектора Е зависит от знака заряда Q: если Q > 0, то вектор Е направлен по радиусу от заряда, если Q < 0, то вектор Е направлен к заряду.
Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор r от заряда Q к точке наблюдения. Тогда при Q > 0 вектор E параллелен r, а при Q < 0 вектор E анти параллелен r. Следовательно, можно записать:
|
где r – модуль радиус-вектора r.
Вопрос 3:
Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. 1 В = 1 Дж/Кл
Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:
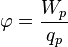
Напряжённость электростатического поля 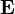 и потенциал
и потенциал 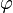 связаны соотношением[1]
связаны соотношением[1]
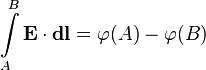
или обратно[2]:
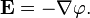
Здесь  — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.
— оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.
4 Энергия системы зарядов
Найдем сначала выражение для потенциальной энергии системы двух точечных зарядов 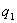 и
и 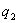 , находящихся на расстоянии
, находящихся на расстоянии 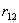 . Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сблизим заряды на заданное расстояние
. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю. Сблизим заряды на заданное расстояние 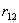 . При этом мы должны будем совершить работу против электрических сил, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая
. При этом мы должны будем совершить работу против электрических сил, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая 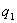 к
к 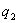 либо
либо 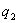 к
к 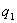 .Работа переноса заряда
.Работа переноса заряда 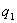 из бесконечности в точку, удаленную от
из бесконечности в точку, удаленную от 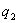 на
на 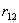

где  - потенциал, создаваемый зарядом
- потенциал, создаваемый зарядом 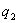 в той точке, в которую перемещается заряд
в той точке, в которую перемещается заряд 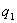 . Аналогично работа переноса заряда
. Аналогично работа переноса заряда 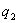 из бесконечности в точку, удаленную от
из бесконечности в точку, удаленную от 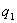 на
на 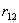 , равна
, равна

где 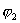 - потенциал, создаваемый зарядом
- потенциал, создаваемый зарядом 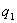 в той точке, в которую перемещается заряд
в той точке, в которую перемещается заряд 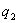 . Значение работ в обоих случаях одинаковы, и каждое из них выражает энергию системы
. Значение работ в обоих случаях одинаковы, и каждое из них выражает энергию системы

Для того чтобы в выражение энергии системы оба заряда входили симметрично, запишем его следующим образом:
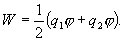
Эта формула дает энергию системы двух зарядов.
Добавляя к системе Зарядов последовательно 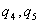 и т.д., можно убедиться в том, что в случае n зарядов потенциальная энергия системы равна
и т.д., можно убедиться в том, что в случае n зарядов потенциальная энергия системы равна
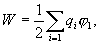
| (16.1) |
где 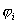 - потенциал, создаваемый в той точке, где находится
- потенциал, создаваемый в той точке, где находится 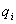 , всеми зарядами, кроме i-го.
, всеми зарядами, кроме i-го.
5 Связь между
Итак, электростатическое поле можно описать либо с помощью векторной величины  , либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее:
, либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее:
Изобразим перемещение заряда q по произвольному пути l (Рис. 3.1) в электростатическом поле  .
.
Работу, совершенную силами электростатического поля на бесконечно малом отрезке d l, можно найти так:
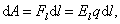
| (3.4.1) |
где El – проекция  на
на 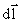 ; d l – произвольное направление перемещения заряда.
; d l – произвольное направление перемещения заряда.
С другой стороны, как мы показали, эта работа, если она совершена электростатическим полем, равна убыли потенциальной энергии заряда, перемещенного на расстоянии d l:
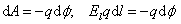 ,
,
отсюда
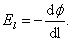
| (3.4.2) |
Для ориентации d l (направление перемещения) в пространстве, надо знать проекции  на оси координат:
на оси координат:
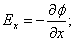


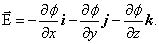
| (3.4.3) |
По определению градиента сумма первых производных от какой-либо функции по координатам есть градиент этой функции, то есть

|
6 Поток вектора
В современной физике потоком вектора а называют скалярную физическую величину
Φа = ∫∫ S а d S = ∫∫ S (а n) d S, (1)
где S – площадь произвольно расположенной поверхности;
а – произвольный вектор, начало которого лежит на поверхности S;
d S = n d S – псевдовектор, поставленный в соответствие ориентированной элементарной площадке (И.Бронштейн и К.Семендяев, 1968);
n – орт нормали к элементарной площадке d S.
Псевдовектор элементарной площадки d S, является чистой математической абстракцией. В статье, посвященной физическому содержанию векторной величины, показано, что согласно принципу причинности произвольную векторную величину а следует рассматривать как локализацию полного вектора, распределенного по площади и приложенного в точке с заданными координатами.
Когда в математике и физике сначала вводят понятие частной величины (локального вектора), а затем – понятие общей величины, называемой потоком вектора, то мы имеем дело с не всегда оправданным применением индуктивного метода (от частного к общему). А дедуктивный метод (от общего к частному) предполагает сначала введение полной величины (неудачно названной в данном случае потоком вектора), а затем уже – введение локализованной величины (самого вектора).
Термин "поток вектора" является, по нашему мнению, отражением неаккуратности в присвоении названий физическим величинам и должен быть заменен другим термином. Процитируем популярный справочник по математике И.Бронштейна и К.Семендяева (1986): " Каждой ориентированной плоской площадке Σ можно поставить в соответствие вектор S, имеющий направление n и модуль, равный ее площади S ".
Приведем пример. На основании приведенной цитаты может показаться, что такая векторная величина, как перемещение объема Δ V, является скаляром, так как определяется скалярным произведением Δ V = х d S. Но приводимое в учебниках по физике указание на то, что "поток вектора скорости" является скалярной величиной, противоречит принципу причинности. Ведь перемещение x центра перемещаемого объема d V является следствием перемещения этого объёма, а не его причиной. При соблюдении принципа причинности следует записать выражение x = d V /d S. И тогда элементарная площадка d S остается скаляром, чем она, по сути дела, и является. А понятие о псевдовекторе площадки d S остается математической абстракцией, не имеющей физического содержания.
Почему же в теории физического поля применяются скалярные потоки вектора? Дело в том, что при анализе физического поля не применяются понятия о проточных системах и перемещаемых координатах состояния, и применение скалярных потоков вектора себя оправдывает теоретически, так как в этом случае оно не противоречит принципу причинности. Но и тут следует заметить, что вместо записи d S, как это принято в векторном анализе, предпочтительнее указывать запись n d S.
В частности, поток вектора магнитной индукции B (магнитный поток) Φm = ∫∫S Bn d S является величиной скалярной, ведь в магнитных цепях никакие энергоносители не перемещаются
7
. Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности
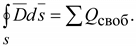 (15.11)
(15.11)
Вектор 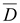 – это такая характеристика поля, которая не зависит от диэлектрических свойств среды.
– это такая характеристика поля, которая не зависит от диэлектрических свойств среды.
2. Так как 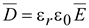 , то теорему Гаусса для однородной и изотропной среды можно записать:
, то теорему Гаусса для однородной и изотропной среды можно записать:
 (15.12)
(15.12)
Вектор 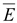 – это характеристика поля, которая зависит от диэлектрических свойств среды.
– это характеристика поля, которая зависит от диэлектрических свойств среды.
3. Поток вектора 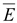 через любую замкнутую поверхность создается не только суммой свободных зарядов, но и суммой связанных зарядов
через любую замкнутую поверхность создается не только суммой свободных зарядов, но и суммой связанных зарядов
 . (15.13)
. (15.13)
Теорему Гаусса можно использовать для нахождения напряженности или электрического смещения в какой-либо точке поля, если через эту точку можно провести замкнутую поверхность таким образом, что все ее точки будут в симметричных (одинаковых условиях по отношению к заряду, находящемуся внутри замкнутой поверхности).
Такой поверхностью являются обычно сфера (если заряд точечный), или боковая поверхность цилиндра (если заряд линейный).
8
| Теорема Остроградского-Гаусса | ||
|
| ||
| Обозначим через G трехмерное тело, ограниченное кусочно-непрерывной, гладкой, замкнутой поверхностью S с внешней нормалью. Предположим, что задано векторное поле
компоненты которого имеют непрерывные частные производные.
где через
обозначена дивергенция векторного поля
В частном случае, полагая
| ||
|
| ||
|
| ||
9
Теорема Гаусса выражает замечательное свойство электрического поля, которое позволяет представить эту теорему в иной форме, расширяющей ее возможности как инструмента исследования и расчета. Найдем дифференциальную форму теоремы Гаусса, в которой устанавливается связь между объемной плотностью заряда p и изменениями напряженности (E) в окрестности данной точки пространства.
Пусть имеем заряд q в объеме V, охватываемом замкнутой поверхностью S, представим его как
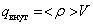 , ,
| (12.1) |
где < r> – среднее по объему V значение объемной плотности заряда. Запишем теорему Гаусса:
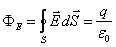 . .
| (12.2) |
Тогда подставим это выражение в (12.1) и разделим обе части равенства на V. В результате получим:
 . .
| (12.3) |
Теперь устремим объем V®0, стягивая его к интересующей нас точке поля. Тогда <r> будет стремиться к значению r в данной точке поля, а левая часть уравнения будет стремиться к /0.
Величину, являющуюся пределом отношения 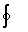 Е dSк V при V0, называют дивергенцией поля Е и обозначают div E. То есть, по определению:
Е dSк V при V0, называют дивергенцией поля Е и обозначают div E. То есть, по определению:
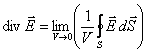 . .
| (12.4) |
Аналогично определяется дивергенция любого другого векторного поля. Из определения (12.4) следует, что дивергенция вектора E является скалярной функцией координат.
Чтобы найти дивергенцию Е надо взять бесконечно малый объем V, определить поток вектора Е сквозь замкнутую поверхность, охватывающую этот объем, и найти отношение этого потока к объему. Полученное выражение для дивергенции поля вектора Е будет зависеть от выбора системы координат (в разных системах координат оно оказывается разным). Если есть декартова система координат (x, y, z), то
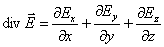 . .
| (12.5) |
Итак, мы выяснили, что при V0 в выражении (8.3) его правая часть стремится к /0, а левая – к div E. Из (12.4) следует, что дивергенция поля Е связана с плотностью заряда в той же точке уравнением:
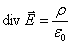 , ,
| (12.6) |
оно и выражает теорему Гаусса в дифференциальной форме.
В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция поля Е в данной точке зависит только от плотности электрического заряда r в той же точке и больше ни от чего.
еще одна форма записи в дифференциальной форме теоремы Гаусса для электростатического поля в вакууме.
Дифференциальная форма записи электростатической теоремы Гаусса – это одно из замечательных свойств электрического поля. Т.е. в разных точках поля точечного заряда поле E отличается друг от друга, это же относится, вообще говоря, и к пространственным производным: Ex/x, Ey/y, Ez/z. Однако, по утверждению теоремы Гаусса, сумма этих производных, которая определяет дивергенцию Е, оказывается во всех точках поля (вне самого заряда) равной нулю. В тех точках поля, где div E >0 (дивергенция Е положительна), мы имеем источники поля (положительные заряды), а там где она отрицательна – стоки (отрицательные заряды).
Линии вектора Е выходят из источников поля, а заканчиваются в местах стоков.
Теорема Остроградского-Гаусса:
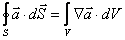 – это соотношение справедливо для любых векторных полей,
– это соотношение справедливо для любых векторных полей,  – векторная величина, характеризующая произвольное векторное поле.
– векторная величина, характеризующая произвольное векторное поле.

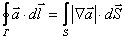 – теорема Стокса:
– теорема Стокса:
Циркуляция вектора  по произвольному замкнутому контуру Г равна потоку вектора rot
по произвольному замкнутому контуру Г равна потоку вектора rot  через произвольную поверхность S, ограниченную данным контуром.
через произвольную поверхность S, ограниченную данным контуром.
Она позволяет найти циркуляцию вектора  по контуру Г, ограничивающему поверхность S (контур может быть не плоским), если известен ротор вектора
по контуру Г, ограничивающему поверхность S (контур может быть не плоским), если известен ротор вектора  в каждой точке некоторой (не обязательно плоской) поверхности S.
в каждой точке некоторой (не обязательно плоской) поверхности S.
Рассмотрим несколько интересных на наш взгляд примеров расчета напряженности или разности потенциалов для электростатического поля.
10 поляризация
Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента.
Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика
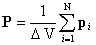 ,
,
Электронный тип поляризации характерен для диэлектриков с неполярными молекулами. Во внешнем электрическом поле (рис. 2.1) положительные заряды внутри молекулы смещаются по направлению поля, а отрицательные в противоположном направлении, в результате чего молекулы приобретают дипольный момент, направленный вдоль внешнего поля
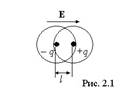
Индуцированный дипольный момент молекулы пропорционален напряженности внешнего электрического поля  , где
, где  - поляризуемость молекулы. Значение поляризованности в этом случае равно
- поляризуемость молекулы. Значение поляризованности в этом случае равно  , где n - концентрация молекул
, где n - концентрация молекул 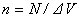 ;
; 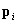 - индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
- индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
Ориентационнный тип поляризации характерен для полярных диэлектриков. В отсутствие внешнего электрического поля молекулярные диполи ориентированы случайным образом, так что макроскопический электрический момент диэлектрика равен нулю.
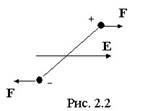
Если поместить такой диэлектрик во внешнее электрическое поле, то на молекулу-диполь будет действовать момент сил (рис. 2.2), стремящийся ориентировать ее дипольный момент в направлении напряженности поля. Однако полной ориентации не происходит, поскольку тепловое движение стремится разрушить действие внешнего электрического поля.
Такая поляризация называется ориентационной. Поляризованность в этом случае равна 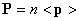 , где < p > - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля.
, где < p > - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля.
Решеточный тип поляризации характерен для ионных кристаллов. В ионных кристаллах (NaCl и т.д.) в отсутствие внешнего поля дипольный момент каждой элементарной ячейки равен нулю (рис. 2.3.а), под влиянием внешнего электрического поля положительные и отрицательные ионы смещаются в противоположные стороны (рис. 2.3.б). Каждая ячейка кристалла становится диполем, кристалл поляризуется. Такая поляризация называется решеточной. Поляризованность и в этом случае можно определить как 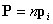 , где
, где 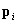 - значение дипольного момента элементарной ячейки, n - число ячеек в единице объема.
- значение дипольного момента элементарной ячейки, n - число ячеек в единице объема.

11
Связанные заряды. В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными. Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью 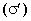 .
.
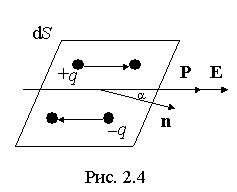
Выделим в поляризованном диэлектрике наклонную призму с основанием S и ребром L, параллельным вектору поляризации P (рис. 2.4). В результате поляризации на одном из оснований призмы появятся отрицательные заряды с поверхностной плотностью 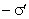 , а на другой положительные заряды с плотностью
, а на другой положительные заряды с плотностью  .
.
С макроскопической точки зрения, рассматриваемый объем эквивалентен диполю, образованному зарядами 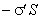 и
и  , которые отстоят друг от друга на расстояние L, тогда электрический момент призмы равен
, которые отстоят друг от друга на расстояние L, тогда электрический момент призмы равен 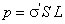 .
.
С другой стороны, электрический момент единицы объема равен 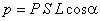 , где
, где  - угол, между направлением нормали к основанию призмы и вектором P. Произведение
- угол, между направлением нормали к основанию призмы и вектором P. Произведение 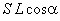 есть объем призмы.
есть объем призмы.
Приравняв друг к другу оба выражения для электрического момента, получаем, что поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации:
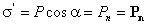 ,
,
где n - единичный вектор нормали к поверхности диэлектрика.
Если вектор поляризации P различен в разных точках объема диэлектрика, то в диэлектрике возникают объемные поляризационные заряды, объемная плотность которых 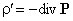 .
.
12
Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике
Из предыдущего раздела следует, что напряженность поля Е при переходе из вакуума в диэлектрик изменяется скачкообразно. Такой же эффект будет наблюдаться при переходе из одного диэлектрика в другой. Скачкообразное изменение вектора 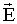 , обусловленное его зависимостью от e, затрудняет расчет полей при решении ряда задач. Поэтому для характеристики электрического поля целесообразно внести векторную величину
, обусловленное его зависимостью от e, затрудняет расчет полей при решении ряда задач. Поэтому для характеристики электрического поля целесообразно внести векторную величину 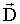 , которая не зависела бы от e. Этот вектор
, которая не зависела бы от e. Этот вектор 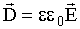 , он называется вектором электрического смещения или электрической индукции. Подставим в последнее соотношение e = 1+æ и получим
, он называется вектором электрического смещения или электрической индукции. Подставим в последнее соотношение e = 1+æ и получим
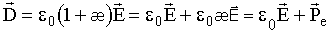 .
.
Обратимся вновь к рисунку 1.19. Внешнее поле 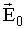 создается свободными зарядами заряженных поверхностей. Внутри диэлектрика действует также поле связанных зарядов, т.е. зарядов, входящих в состав атомов и молекул диэлектрика. Заряды, не связанные с перечисленными выше частицами диэлектрика, называют свободными. Это: а) заряды частиц, способных перемещаться под действием электрического поля на макроскопические расстояния (электронов проводимости в металлах, электронов в вакууме, ионов в электролитах и т.п.); б) положительные заряды атомных остатков в металлах; в) избыточные заряды, сообщенные телу и нарушающие его электрическую нейтральность (например, заряды, нанесенные извне на поверхность диэлектрика).
создается свободными зарядами заряженных поверхностей. Внутри диэлектрика действует также поле связанных зарядов, т.е. зарядов, входящих в состав атомов и молекул диэлектрика. Заряды, не связанные с перечисленными выше частицами диэлектрика, называют свободными. Это: а) заряды частиц, способных перемещаться под действием электрического поля на макроскопические расстояния (электронов проводимости в металлах, электронов в вакууме, ионов в электролитах и т.п.); б) положительные заряды атомных остатков в металлах; в) избыточные заряды, сообщенные телу и нарушающие его электрическую нейтральность (например, заряды, нанесенные извне на поверхность диэлектрика).
Электрическое поле в диэлектрической среде создается как свободными, так и связанными зарядами. Первичным источником поля являются свободные заряды, а поле связанных зарядов возникает в результате поляризации диэлектрика при помещении его в поле свободных зарядов. Причем, поле связанных зарядов может вызвать перераспределение свободных зарядов и изменить поле этих зарядов.
Поэтому вектор 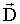 характеризует электростатическое поле, создаваемое свободными зарядами в вакууме (e=1), но при таком их распределении в пространстве, какое будет при наличии диэлектрика. Линии вектора
характеризует электростатическое поле, создаваемое свободными зарядами в вакууме (e=1), но при таком их распределении в пространстве, какое будет при наличии диэлектрика. Линии вектора 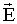 начинаются и заканчиваются на любых зарядах - свободных и связанных, а линии вектора
начинаются и заканчиваются на любых зарядах - свободных и связанных, а линии вектора 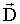 - только на свободных зарядах и они проходят диэлектрик не прерываясь. Смысл введения вектора электрического смещения состоит в том, что поток вектора
- только на свободных зарядах и они проходят диэлектрик не прерываясь. Смысл введения вектора электрического смещения состоит в том, что поток вектора 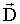 через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами, находящимися внутри объема, ограничивающего данную поверхность S (как это было с потоком
через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами, находящимися внутри объема, ограничивающего данную поверхность S (как это было с потоком 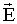 ). Это позволяет не рассматривать связанные (поляризованные) заряды и упрощает решение многих задач.
). Это позволяет не рассматривать связанные (поляризованные) заряды и упрощает решение многих задач.
Поток вектора 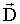 через произвольную замкнутую поверхность S равен
через произвольную замкнутую поверхность S равен 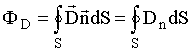 , где Dn - проекция вектора
, где Dn - проекция вектора 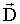 на нормаль
на нормаль 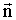 к площадке dS. Теорема Гаусса для электростатического поля в диэлектрике выводится аналогично выводу теоремы для вакуума, в результате получаем
к площадке dS. Теорема Гаусса для электростатического поля в диэлектрике выводится аналогично выводу теоремы для вакуума, в результате получаем 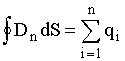 , где в правой части сумма свободных зарядов.
, где в правой части сумма свободных зарядов.
13
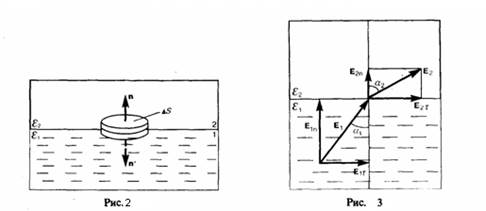
Исследуем связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (у которых диэлектрические проницаемости равны ε1 и ε2) при отсутствии на границе свободных зарядов.
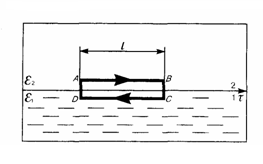
Рис.1
Проведем вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l, с направлением ориентации, как показано на рис. 1. По теореме о циркуляции вектора Е, применительно к данному случаю
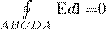
откуда
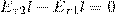
(знаки интегралов по АВ и CD разные, поскольку пути интегрирования противоположны, а интегралы по участкам ВС и DA малы). Поэтому
 (1)
(1)
Заменив проекции вектора Е проекциями вектора D, деленными на ε0ε, получим
 (2)
(2)
построим прямой цилиндр ничтожно малой высоты на границе раздела двух диэлектриков (рис. 2); одно основание цилиндра находится в первом диэлектрике, другое — во втором. Основания ΔS настолько малы, что в пределах каждого из них вектор D одинаков. Согласно теореме Гаусса для электростатического поля в диэлектрике
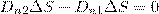
(нормали n и n' к основаниям цилиндра противоположно направлены). Поэтому
 (3)
(3)
Заменив проекции вектора D проекциями вектора Е, умноженными на ε0ε, получим
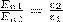 (4)
(4)
Значит, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е (Еτ) и нормальная составляющая вектора D (Dn) изменяются непрерывным образом (не испытывают скачка), а нормальная составляющая вектора Е (Еn) и тангенциальная составляющая вектора D (Dτ) испытывают скачок.
Из условий (1) — (4) для составляющих векторов Е и D мы видим, что линии этих векторов испытывают излом (преломляются). Найдем как связаны между углы α1 и α2 (на рис. 3 α1>α2). Используя (1) и (4), Еτ2 = Еτ1 и ε2En2 = ε1En1. Разложим векторы E1 и E2 на тангенциальные и нормальные составляющие у границы раздела. Из рис. 3 мы видим, что

Учитывая записанные выше условия, найдем закон преломления линий напряженности Е (а значит, и линий смещения D)

Из этой формулы можно сделать вывод, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали.
14
Вещество или материальное тело, в котором имеются заряды, способные переносить электрический ток, называется проводником. В металлах переносчиками тока служат свободные (т.е. не привязанные к атомам) электроны, в электролитах — ионы, в плазме — и электроны, и ионы. Для электростатических явлений поле внутри проводника равно нулю:
15
15. Электрическая ёмкость. Конденсаторы.
Электрическая емкость характеризует способность тела или системы тел накапливать электрические заряды, запасая таким образом энергию электрического поля.
Емкость определяют как отношение заряда уединенного проводящего тела к его потенциалу(при условии, что точка, в которой потенциал принимается равным нулю, лежит в бесконечности):
С = q/U,
а емкость двух проводящих тел, разделенных диэлектриком и заряженных равными по значению и противоположными по знаку зарядами – как отношение абсолютного значения заряда к разности потенциалов этих тел:
С=q/(U1 – U2).
(1.15)
Емкость зависит от геометрических размеров, конфигурации, диэлектрической проницаемости диэлектрика и взаимного расположения тел.
Емкость измеряется в Фарадах (Ф).
Конденса́тор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкции состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).
16. Энергия заряженного конденсатора
Если на обкладках конденсатора электроемкостью С находятся электрические заряды +q и -q, то напряжение между обкладками конденсатора = U=q/C. В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0. Ср. значение напряжения в процессе разрядки = Uср=U/2=q/2C. Для работы А, соверш. эл. полем при разрядке конденсатора: A=qUср=qU/2=CU^2/2. => потенциальная энергия Wp конденсатора электроемкостью С, заряженного до напряжения U:Wp=A= CU^2/2=q^2/2C=qU/2. Энергия конденсатора обусловлена тем, что эл. поле между его обкладками обладает энергией. Напряженность Е поля пропорц. U => энергия электрического поля пропорциональна квадрату его напряженности.
17
Опыт показывает, что заряженный конденсатор содержит запас энергии.
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую (рис. 1.7.1). При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов 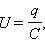 при переносе каждой порции Δq внешние силы должны совершить работу
при переносе каждой порции Δq внешние силы должны совершить работу 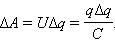
Энергия Wе конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

|
Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.
|
Электрическую энергию Wе следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. Формулы для Wе аналогичны формулам для потенциальной энергии Eр деформированной пружины (см. ч. I, § 2.4)

|
где k – жесткость пружины, x – деформация, F = kx – внешняя сила.
По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Это легко проиллюстрировать на примере заряженного плоского конденсатора.
Напряженность однородного поля в плоском конденсаторе равна E = U/d, а его емкость 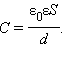 Поэтому
Поэтому
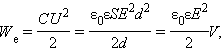
|
где V = Sd – объем пространства между обкладками, занятый электрическим полем. Из этого соотношения следует, что физическая величина
|
является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.
Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности wе по всему объему, в котором создано электрическое поле.
Вопрос 18
Электрический ток. Сила и плотность тока
Электрическим током называется направленное (упорядоченное) движение заряженных частиц.
Электрический ток в проводниках различного рода представляет собой либо направленное движение электронов в металлах (проводники первого рода), имеющих отрицательный заряд, либо направленное движение более крупных частиц вещества — ионов, имеющих как положительный, так и отрицательный заряд — в электролитах (проводники второго рода), либо направленное движение электронов и ионов обоих знаков в ионизированных газах (проводники третьего рода).
За направление электрического тока условно принято направление движения положительно заряженных частиц.
Для существования электрического тока в веществе необходимо:
- наличие заряженных частиц, способных свободно перемещаться по проводнику под действием сил электрического поля:
- наличие источника тока, создающего и поддерживающего в проводнике в течение длительного времени электрическое поле;
Количественными характеристиками электрического тока являются сила тока I и плотность тока j.
Сила тока — скалярная физическая величина, определяемая отношением заряда Δq, проходящего через поперечное сечение проводника за некоторый промежуток времени Δt, к этому промежутку времени.
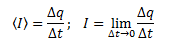
Единицей силы тока в СИ является ампер (А).
Если сила тока и его направление со временем не изменяются, то ток называется постоянным.
Единица силы тока — основная единица в СИ 1 А — есть сила такого неизменяющегося тока, который, проходя по двум бесконечно длинным параллельным прямолинейным проводникам очень маленького сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывает силу взаимодействия между ними 2·10-7 Η на каждый метр длины проводников.
Плотность тока j — это векторная физическая величина, модуль которой определяется отношением силы тока I в проводнике к площади S поперечного сечения проводника, т.е.
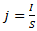
В СИ единицей плотности тока является ампер на квадратный метр (А/м2).
Как следует из формулы (1), 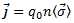 . Направление вектора плотности тока
. Направление вектора плотности тока 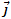 совпадает с направлением вектора скорости упорядоченного движения
совпадает с направлением вектора скорости упорядоченного движения  положительно заряженных частиц. Плотность постоянного тока постоянна по всему поперечному сечению проводника.
положительно заряженных частиц. Плотность постоянного тока постоянна по всему поперечному сечению проводника.
Вопрос 19


Вопрос 20
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
|
где R = const.
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
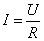
| (7.6.1) |
Для однородного линейного проводника выразим R через ρ:
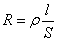 , ,
| (7.6.2) |
ρ – удельное объемное сопротивление; [ρ] = [Ом·м].
Найдем связь между 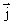 и
и 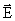 в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока 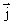 и вектор напряженности поля
и вектор напряженности поля 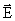 коллинеарны (рис. 7.6).
коллинеарны (рис. 7.6).

Рис. 7.6
Исходя из закона Ома (7.6.1), имеем:
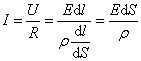
А мы знаем, что 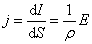 или
или 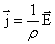 . Отсюда можно записать
. Отсюда можно записать
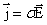
это запись закона Ома в дифференциальной форме.
Здесь 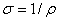 – удельная электропроводность.
– удельная электропроводность.
Размерность σ – [  ].
].
21
Полную цепь можно рассматривать как последовательное соединение сопротивления внешней цепи и внутреннего сопротивления источника тока. Полное сопротивление цепи представляет собой сумму внутреннего сопротивления источника и сопротивления внешней цепи. Заменим элемент каким-либо другим, имеющим такое же внутреннее сопротивление, но другую э. д. с. Мы обнаружим, что ток при этом изменится.
Таким образом, ток в цепи зависит от э. д. с. источника и от полного сопротивления цепи.
Количественный закон, связывающий эти величины, представляет закон Ома для замкнутой цепи: ток в цепи, содержащей источник тока, прямо пропорционален э. д. с. источника и обратно пропорционален полному сопротивлению цепи.
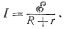 (80.1)
(80.1)
Вопрос 22
Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через каждое сечение проводника проходит заряд 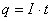 . Это равносильно тому, что заряд q переносится за время t из одного конца проводника в другой.
. Это равносильно тому, что заряд q переносится за время t из одного конца проводника в другой.
При этом силы электростатического поля и сторонние силы, действующие на данном участке, совершают работу 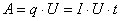 . Разделив работу на время t, за которое она совершается, получим мощность, развиваемую током на рассматриваемом участке
. Разделив работу на время t, за которое она совершается, получим мощность, развиваемую током на рассматриваемом участке 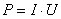 .
.
Эта мощность может расходоваться на совершение работы над внешними телами; на протекание химических реакций; на нагревание данного участка цепи и др.
В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Принято говорить, что при протекании тока в проводнике выделяется тепло
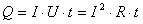 (4.1)
(4.1)
Это соотношение называется законом Джоуля - Ленца. Оно было экспериментально установлено английским физиком Д. П. Джоулем и подтверждено точными опытами Э. Х. Ленца.
Если сила тока изменяется со временем, то количество теплоты, выделяющееся в проводнике за время t, вычисляется по формуле
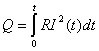 .
.
От формулы (4.1), можно перейти к выражению, характеризующему выделение тепла в различных точках проводника. Выделим в проводнике элементарный объем в виде цилиндра. Согласно закону Джоуля - Ленца, за время d t, в этом объеме выделится количество теплоты
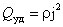 .
.
Величину  называют удельной тепловой мощностью тока. Эта формула представляет собой дифференциальную форму закона Джоуля - Ленца.
называют удельной тепловой мощностью тока. Эта формула представляет собой дифференциальную форму закона Джоуля - Ленца.
Вопрос 23
Вопрос 24
В 1820 г. французские физики Жан Батист Био и Феликс Савар, провели исследования магнитных полей токов различной формы. А французский математик Пьер Лаплас обобщил эти исследования. Он проанализировал экспериментальные данные и сделал вывод, что магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока:
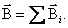
Элемент тока длины d l (рис. 1.4) создает поле с магнитной индукцией:
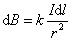 , ,
| (1.2.1) |
или в векторной форме:
 , ,
| (1.2.2) |
Это и есть закон Био–Савара–Лапласа, полученный экспериментально.
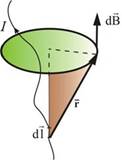
Рис. 1.4
Здесь I – ток; 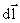 – вектор, совпадающий с элементарным участком тока и направленный в ту сторону, куда течет ток;
– вектор, совпадающий с элементарным участком тока и направленный в ту сторону, куда течет ток; 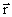 – радиус-вектор, проведенный от элемента тока в точку, в которой мы определяем
– радиус-вектор, проведенный от элемента тока в точку, в которой мы определяем 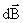 ; r – модуль радиус-вектора; k – коэффициент пропорциональности, зависящий от системы единиц.
; r – модуль радиус-вектора; k – коэффициент пропорциональности, зависящий от системы единиц.
Как видно из рисунка, вектор магнитной индукции 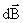 направлен перпендикулярно плоскости, проходящей через
направлен перпендикулярно плоскости, проходящей через 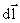 и точку, в которой вычисляется поле.
и точку, в которой вычисляется поле.
Направление 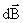 связано с направлением
связано с направлением 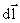 «правилом буравчика»: направление вращения головки винта дает направление
«правилом буравчика»: направление вращения головки винта дает направление 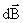 , поступательное движение винта соответствует направлению тока в элементе.
, поступательное движение винта соответствует направлению тока в элементе.
Таким образом, закон Био–Савара–Лапласа устанавливает величину и направление вектора 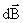 в произвольной точке магнитного поля, созданного проводником
в произвольной точке магнитного поля, созданного проводником 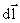 с током I.
с током I.
Модуль вектора 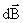 определяется соотношением:
определяется соотношением:
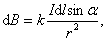 , ,
| (1.2.3) |
где α – угол между 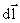 и
и 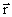 ; k – коэффициент пропорциональности, зависящий от системы единиц.
; k – коэффициент пропорциональности, зависящий от системы единиц.
В международной системе единиц СИ закон Био–Савара–Лапласа для вакуума можно записать так:
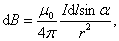 , ,
| (1.2.4) |
где 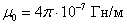 – магнитная постоянная.
– магнитная постоянная.
Вопрос 25

Рис. 1.2. К выводу закона Био–Савара–Лапласа
Вектор dB направлен в точке A перпендикулярно плоскости векторов dl и r по правилу буравчика и совпадает с касательной к линии магнитной индукции.
Магнитное поле прямого тока – тока, текущего по тонкому прямому проводу бесконечной длины. В произвольной точке А, удаленной от оси проводника на расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей.
В качестве постоянной интегрирования выберем угол (угол между векторами dl и r), выразив через него все остальные величины. Из рис.1.2 следует, что
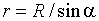 ,
, 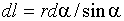 (1.6)
(1.6)
(радиус дуги CD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (1.5), получим, что магнитная индукция, создаваемая одним элементом проводника, равна:
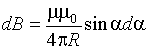 .
.
Так как угол α для всех элементов прямого тока изменяется в пределах от 0 до , то, согласно (1.4) и (1.6),
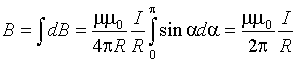 .
.
Следовательно, магнитная индукция поля прямого тока
 .
.
Магнитное поле в центре кругового проводника с током (рис. 1.3).
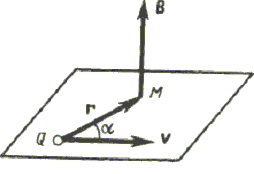
Рис. 1.3. Ориентация векторов B, r и v
Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления – вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin = 1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то
 .
.
Тогда
.
Следовательно, магнитная индукция поля в центре кругового проводника с током:

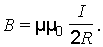
Вопрос 27
Сила Ампера
Действие магнитного поля на проводник с током исследовал экспериментально Андре Мари Ампер (1820 г.). Меняя форму проводников и их расположение в магнитном поле, Ампер сумел определить силу, действующую на отдельный участок проводника с током (элемент тока). В его честь эту силу назвали силой Ампера.
§ Сила Ампера — это сила, с которой магнитное поле действует на помещенный в него проводник с током.
Согласно экспериментальным данным модуль силы F:
пропорционален длине проводника l, находящегося в магнитном поле;
пропорционален модулю индукции магнитного поля B;
пропорционален силу тока в проводнике I;
зависит от ориентации проводника в магнитном поле, т.е. от угла α между направлением тока и вектора индукции магнитного поля B→.
Тогда:
модуль силы Ампера равен произведению модуля индукции магнитного поля B, в котором находится проводник с током, длины этого проводника l, силы тока I в нем и синуса угла между направлениями тока и вектора индукции магнитного поля
FA=I⋅B⋅l⋅sinα,
§ Этой формулой можно пользоваться:
если длина проводни
 2020-08-05
2020-08-05 535
535
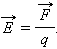
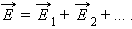
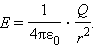
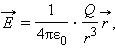

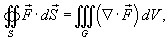
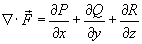
 (она обозначается также символом
(она обозначается также символом  ). Символ
). Символ 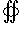 указывает, что поверхностный интеграл вычисляется по замкнутой поверхности.
указывает, что поверхностный интеграл вычисляется по замкнутой поверхности. 
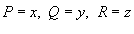 , получаем формулу для вычисления объема тела G:
, получаем формулу для вычисления объема тела G: