Логарифм единицы при любом основании равен нулю

Действительно, из равенства х = а^у следует, что

при y = 0     х = а = 1, т. е. при х= 1     y = 0.

Это означает, что функция у = log_a x имеет единственный корень х = 1.

Таким образом, log_a 1 = 0.

 

Свойство 3.

Логарифм самого основания равен единице.

В самом деле, log_a a = l, так как а¹ = а.

 

Первые три свойства имеют место как

при а > 1,                    так и при   0 < а < 1.

При установлении дальнейших свойств эти два случая будем различать.

 

Свойство 4.

При а > 1 функция y = log_ax    монотонно возрастает,

а при   а < 1 – функция y = log_ax  монотонно убывает.

 

Возьмем два положительных значения аргумента х ₂ > x ₁. Согласно основному логарифмическому тождеству:

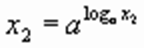и ,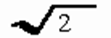

так как     x² > x¹,            то >

 

В силу свойства монотонностипоказательной функции имеем:

log_a x ₂ > log _a x _{1 ,}                если a > 1,

         и   log_a x ₂ < log_a x ₁,                   если a < 1,

что и требовалось доказать.

 

 

Свойство 5.

При а > 1

- значения функции y = log_a x   отрицательны, если 0 < х < 1,

- значения функции y = log_a x   положительны, если х > 1;

При а < 1

- значения функции y = log_a x положительны, если 0 < x < 1,

- значения функции y = log_a x   отрицательны, если х> 1.

 

Докажем справедливость этого свойства.

Корень х= 1 разбивает область определения функции y=log_ax на два промежутка: 0 < x < 1 и 1 < x + .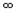

Определим знаки логарифмической функции в этих промежутках:

а > 1 1) из неравенства х < 1 на основании свойства монотонности имеем logaх< loga1 или logaх < 0     2) из неравенства х > 1, cледует, что   loga x > loga1 или logax > 0

а > 1 1) из неравенства х < 1 в соответствии со свойством монотонности имеем logaх > loga1 или logax > 0   2) из неравенства х < 1, cледует, что   loga x < loga1 или logax < 0