Логарифмическая функция

Показательная и логарифмическая функции,

Их графики и свойства

ПОВТОРЕНИЕ

Конспектировать данный материал в тетрадь по математике – не надо.

Конспектировать только тем студентам, у которых в тетради по математике материал по данной теме – отсутствует.

Показательная функция.

Логарифмическая функция.

 

1. Показательная функция, ее график и свойства

 

Функция вида y = a^x,

где а – постоянное, отличное от единицы, положительное число, называется показательной.

Областью ее определения является все множество действительных чисел, так как выражение a ^x при a > 0 имеет смысл при всех действительных значениях x.

 

Показательная функция (экспонента) – э то функция вида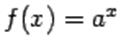        

 

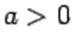
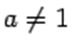
Для неё 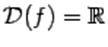, , 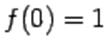, 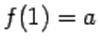и при

график имеет такой вид:

Рис. График показательной функции при

 

При 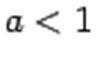 вид графика:

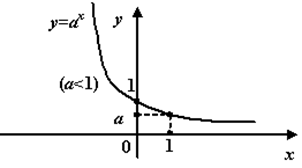
Рис. График показательной функции при

 

Число 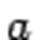 называется основанием показательной функции.

 

Установим свойства показательной функции:

 

Свойство 1. Функция y = a^x принимает только положительные значения.

Для доказательства справедливости этого утверждения рассмотрим четыре случая:

1. х – натуральное число или нуль.

Если х = 1, то а^х = а ¹ = а > 0;

Если x = n, где , то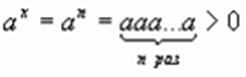

 

При х = 0 а^х = а ⁰ = 1 > 0

 

2. Если x = m/n, где m и n натуральные числа, то а^х= a^m/n > 0 по определению степени с положительным рациональным показателем;

 

3. x –  иррациональное положительное число. По определению степени с иррациональным положительным показателем,

при а > 1

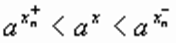при    0 < a < 1,

Где и — рациональные положительные числа. На основании п. 2. 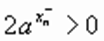и .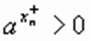

Так как а^х заключено между двумя положительными числами, то оно также число положительное;

 

4. х — действительное отрицательное число.

Пусть x = -t,   где t > 0.

Тогда имеем a^x=a^-t=1/a^t > 0.

Так как a > 0 на основании п. 1-3.

Итак, a^x > 0 при любом действительном значении х. Это свойство имеет место как при a > 1, так и при 0 < a < 1.

 

Свойство 2.

При a > 1 имеем: a^x > 1, если x > 0, и

                           a^x < 1, если x < 0,

При a < 1 имеем: a^x < 1, если x > 0, и

                          a^x > 1, если x < 0.

 

Докажем это свойство для a > 1.

Рассмотрим следующие случаи:

Если x = n (n -натуральное число), то

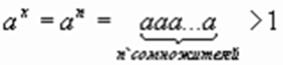
Если x = m/n (m и n – натуральные числа), то

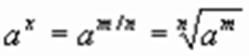
По доказанному выше, a^m > 1; тогда 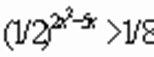, т. е. 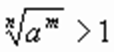, следовательно a^x > 1;

Если х — иррациональное положительное число. По определению степени с положительным иррациональным показателем при a > 1 имеем

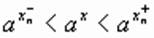
На основании п.2. , поэтому и подавно a^x > 1

Итак, доказано,

что для a > 1 при x > 0 значения функции a^x > 1;

Если х — любое действительное отрицательное число.

Пусть x = -t, где t > 0; тогда a^x = a^-t = 1/ a^t < 1, так как, по доказанному выше, a^t > 1. Аналогично это свойство доказывается для a < 1.

 

Свойство 3.

При a > 1 функция y = a^x монотонно возрастает, а

при a < 1 – монотонно убывает.

Докажем это свойство для a > 1.

Возьмем два значения аргумента х₁ и х₂, причем x ₂ > x ₁. Докажем, что .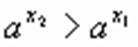

Исследуя разность ,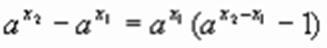

Имеем:  (на основании свойства 1);

х_{2 -} х₁> 0, так как x ₂ > x ₁, 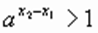(на основании свойства 2),

следовательно .

Произведение , т. е. 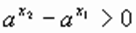таким образом , что и требовалось доказать. Аналогично доказывается это свойство для a < 1.

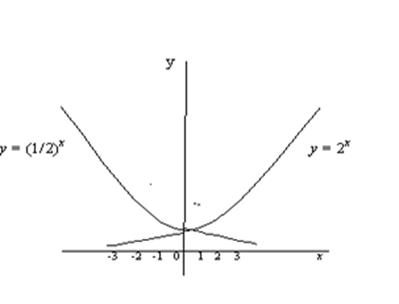
рис. 1

 

 

2. Логарифмическая функция, ее график

И свойства

 

Логарифмическая функция –

это функция вида

                    

Для неё , , ,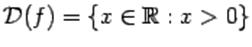

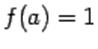и при график имеет такой вид:

 

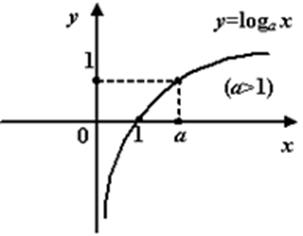
Рис.График логарифмической функции при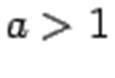

 

 

При 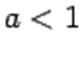 график получим следующего вида:

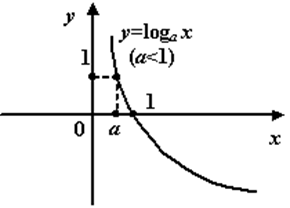
Рис. График логарифмической функции при

 

Число 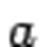 называется основанием логарифма.

Обратим внимание читателя на то, что с точностью до поворотов и симметричных отражений на последних четырёх чертежах изображена одна и та же линия.

 

Рассмотрим показательное уравнение где

а — основание степени;

N — степень;

переменная х — показатель степени.

 

Требуется по данной степени и данному основанию степени найти показатель степени, т. е. корень данного уравнения.

Решим это уравнение графически.

Для этого построим график функции у = а^х и y = N (рис. 77), а затем найдем абсциссу их общей точки.

Очевидно, что при N > 0 это уравнение имеет единственный корень, который обозначается так: log_aN, т. е.

x = log_aN

По определению корня уравнения имеем тождество

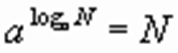(1)

которое выражает определение логарифма

рис.

 

Определение.

Логарифмом данного числа N по данному основанию а называется показатель степени, в которую надо возвести основание а, чтобы получить число N.

К понятию логарифма мы пришли, рассматривая уравнение

a^x = N,

где а > 0, а 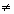1 и N>0. Этими неравенствами определяются допустимые значения а и N в (1).

Равенство (1) называется основным логарифмическим тождеством.

Подчеркнем, что по определению логарифма из равенства

a^x = N

следует равенство х = log_aN;

обратно: из равенства х = log_a N вытекает равенство a^x = N.

 

Действие, с помощью которого находится показатель степени по данной степени и данному основанию степени, называется логарифмированием.

Таким образом, уравнение a^x = N решается логарифмированием.

 

 

Функция вида y = log_ax,

где а > 0 и а 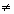1, называется логарифмической.

 

Равенство у = log_a х выражает ту же зависимость между х и у, что и равенства а^у = х и х = а^у.

Так как a^y > 0 (на основании свойства 1 показательной функции), то из равенства а^у = х следует, что х > 0.

 

Таким образом, областью определения логарифмической функции является все множество положительных чисел.

 

Связь показательной и логарифмической функций иллюстрирует следующая таблица:

	x	y
у=ах	Показатель степени	Степень
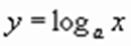(x = ay)	Степень	Показатель степени

 

Показательная функция характеризует изменение степени в зависимости от изменения показателя степени,

Логарифмическая функция характеризует изменение показателя степени в зависимости от изменения степени.

Поэтому эти функции называют взаимно обратными.

На основании свойств показательной функции установим свойства логарифмической функции.

 

Свойство 1.

Функция у = log_a х может принимать любые действительные значения: — 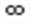 <y < + .

Действительно, в равенстве х = а^у показатель у – любое действительное число (на основании свойства показательной функции), значит, рассматриваемое свойство справедливо.

 

Свойство 2.