Доказательство формул двойного угла

Формулы двойного угла в тригонометрии.

Формулы двойного угла выражают синус, косинус, тангенс и котангенс угла 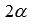через тригонометрические функции угла 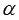. В этой статье мы сначала перечислим все формулы двойного угла, после чего приведем их доказательство. Дальше рассмотрим несколько примеров применения. В заключение остановимся на формулах тройного, четверного и так далее углов.

Список формул двойного угла

Прежде чем дать все формулы двойного угла напомним, что в тригонометрии при записи синуса, косинуса, тангенса и котангенса кратных углов вида 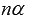, где n – некоторое натуральное число, аргумент 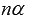принято записывать без скобок. При этом, например, запись 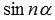понимают как 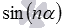. Также стоит напомнить, что запись 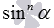понимается как 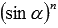, аналогичные записи используются и для косинуса, и для тангенса, и для котангенса в степени n.

Теперь запишем все формулы двойного угла в виде списка.

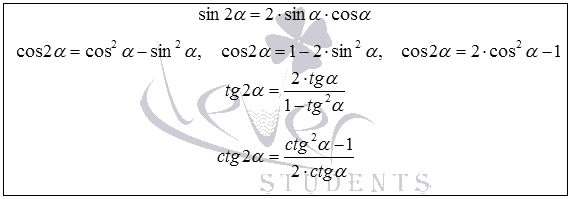
Заметим, что формулы синуса и косинуса двойного угла справедливы для любого угла 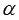. Формула тангенса двойного угла имеет место для любых 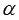, при которых определен 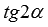(то есть, при 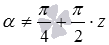, где z – любое целое число). В свою очередь формула котангенса двойного угла справедлива для любых 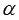, при которых имеет место 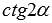(то есть, при ).

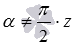Привлекает внимание тот факт, что для косинуса двойного угла записаны три формулы. Все они равносильны, и употребляются примерно одинаково часто в зависимости от требований конкретной задачи.

К началу страницы

Доказательство формул двойного угла

Формулы двойного угла доказываются достаточно просто – они следуют из формул сложения. Действительно, возьмем формулы синуса суммы 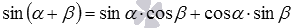и косинуса суммы 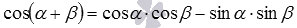, и положим в них 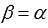. При этом получим и, так доказаны формулы синуса и косинуса двойного угла вида 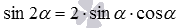и .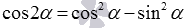

Две другие формулы косинуса двойного угла вида 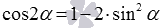и 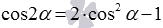сводятся к формуле 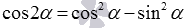, если в них единицу заменить на сумму квадратов синуса и косинуса на основе основного тригонометрического тождества 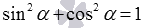. Так и.

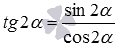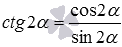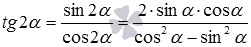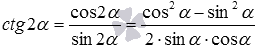Осталось доказать формулы тангенса и котангенса двойного угла. Для этого используем равенства и , а также формулы синуса и косинуса двойного угла. Имеем и . Осталось числитель и знаменатель первой дроби разделить на 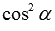(здесь нужно заметить, что 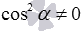при тех значениях 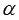, при которых определен 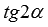, поэтому мы избежим деления на нуль), а второй – на 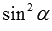( 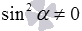при тех значениях 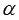, при которых определен 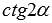). Осталось лишь завершить доказательство формул двойного угла для тангенса и котангенса: