IV. Наименьшее и наибольшее значения линейной

ФУНКЦИИ НА МНОГОГРАННИКЕ

Рассмотрим линейную целевую функцию двух переменных F = c₁x₁ + c₂x₂, область определения которой задается совместной системой линейных неравенств с двумя переменными, т.е.   

a_i1x₁ + a_i2x₂ <= b_i; i= 1,2,…, m   ( 1),  

где c₁, c₂, a_i1, a_i2, b_i – заданные числа.

Предположим, что мы исключили все «лишние неравенства».

Найдем те точки многоугольника решений, при которых рассматриваемая линейная функция  F  имеет наименьшее и наибольшее значение.

Линиями уровня линейной функции F (т.е. линиями, в каждой точке которых функция имеет одно и тоже значение) являются прямые, уравнения которых имеют вид

c₁x₁ + c₂x₂ = F₁,

 

где F₁ - значение линейной функции на соответствующей прямой.

Прямая c₁x₁ + c₂x₂ = F₁, перпендикулярна вектору–градиенту 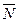= (с₁, с₂) (рис.10)

Координаты конечной точки вектора-градиента равны частным производным выражения целевой функции:

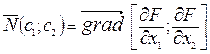
Вектор-градиент и линии уровня взаимно перпендикулярны. Длина вектора-градиента при графическом методе решения задач роли не играет, важно только его направление.

 

Рис. 10

 

Рассмотрим прямую, перпендикулярно к вектору N и станем ее перемещать параллельно самой себе. Пусть при перемещении прямой она впервые встретит многоугольник в вершине А, в этом положении прямая будет опорной. При дальнейшем перемещении в том же направлении прямая пройдет через вершину В и тоже будет опорной. Так как направление вектора 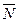 есть направление наибольшего возрастания линейной функции  F, то на опорной прямой U₁  функция F имеет наименьшее значение, а на опорной прямой  U₂ - наибольшее значение (среди всех значений функций  F, принимаемых на многограннике решений).

Следовательно, наименьшее и наибольшее значение линейной функции F = c₁x₁ + c₂x₂ на многоугольнике решений достигается в точках пересечения этого многоугольника с опорными прямыми, перпендикулярными к вектору. Пересечение опорной прямой с многоугольником решений может состоять либо из одной точки (вершины), либо из бесчисленного множества точек (сторон).

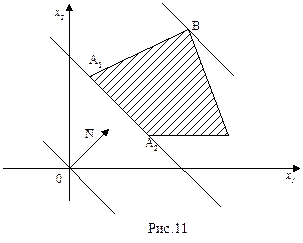На рисунке 11 представлен случай, когда линейная функция имеет наибольшее значение в точке В и наименьшее значение в каждой точке стороны А₁А₂.

 

Аналогично, для линейной функции трех переменных

F = c₁x₁ + c₂x₂ + c₃x₃

наименьшее и наибольшее значение функции на многограннике решений достигаются в точках пересечения этого многогранника с опорными плоскостями

 c₁x₁ + c₂x₂ + c₃x₃ = Fk

перпендикулярными вектору 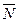=(c₁, c₂, c₃). На одной из опорных плоскостей функция F имеет наименьшее значение, а на другой – наибольшее (рис. 12).

Как видно из рисунка, плоскости, соответствующие различным значениям целевой функции параллельны друг другу. Отсюда следует, что никакой точке, лежащей строго внутри многогранника решений, не может соответствовать оптимальное решение, так как всегда найдутся точки, которые лежат на гиперплоскостях, соответствующих большим значениям целевой функции. Значит решение нужно искать на ребрах,гранях или вершинах многогранников.

Обобщением понятия линейных функций двух и трех переменных является линейная функция: F = c₁x₁ + c₂x₂ + … + c_nx_n   от п- переменных.

Множество точек, в которых линейная функция F имеет наименьшее (соответственно наибольшее) значение, есть пересечение «многогранника решений» с опорной плоскостью c₁x₁+…+c_nx_n=F_min (соответственно с опорной плоскостью c₁x₁+…+c_nx_n=F_max) через F_min и F_max обозначены соответственно наименьшее и наибольшее значения функции F на многограннике решений.