2020-08-05
166
ПРОГРАММИРОВАНИЯ
Графический метод удобен тем, что он обладает большой наглядностью. Неудобство графического метода заключается в том, что он применяется к задачам небольшой размерности, обычно не более трех переменных. Графический метод реализует решение задачи, записанной в однородной форме.
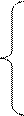a11х1 + а12х2 ≤ b1
a21x1 + a22x2 ≤ b2 x1 ≥ 0; x2 ≥ 0.
am1x1 + am2x2 ≤ bm
max Z = c1x1 + c2x2
Геометрический смысл неравенства ai1x1 + ai2x2 ≤ bi.
Неравенство ai1x1 + ai2x2 ≤ bi определяет граничную прямую ai1x1 + ai2x2 =bi, которая делит плоскость на две полуплоскости: положительную ai1x1 + ai2x2 > bi и отрицательную
ai1x1 +ai2x2 < bi. Для того, чтобы построить ограничение–неравенство, необходимо построить граничную прямую ai1x1 + ai2x2 = bi по двум точкам, а затем определить полуплоскость, удовлетворяющую данному неравенству. Если граничная прямая не проходит через начало координат, то для определения полуплоскости удобно в неравенство подставить координаты точки начала координат – О(0,0). Если неравенство при этом выполняется, то начало координат входит в полуплоскость. Если начало координат принадлежит граничной прямой, то для определения искомой полуплоскости подставляют в данное неравенство координаты любой точки, не принадлежащей граничной прямой.
|
|
|
Например, необходимо определить полуплоскость для неравенства 3х1 + 2х2 ≤ 6. На плоскости координат (рис.13) строим граничную прямую, определяемую равенством 3х1+ 2х2=6, по двум точкам А(0, 3) и В(2,0). Граничная прямая не проходит через начало координат, поэтому представляем координаты точки О(0,0) в неравенство. Получаем верное неравенство 3*0+2*0<6 (0<6), следовательно, начало координат входит в полуплоскость неравенства 3х1 + 2х2 ≤ 6. Полуплоскость, удовлетворяющую неравенству, будем отмечать штриховкой.
 |
Область допустимых решений
Областью допустимых решений является пересечение плоскостей, определяющих все неравенства (ограничения) системы ограничений задачи и условия неотрицательности переменных. Поэтому, для нахождения области допустимых решений необходимо построить плоскости для каждого ограничения и для условия неотрицательности переменных и определить область, принадлежащую всем плоскостям.
1. Остановимся на простом геометрическом методе линейного програмирования, имеющем большую наглядность. Этот метод может быть использован лишь для решения простых задач с малым числом переменных.
Пример. Математическая модель задачи представляется системой ограничений:
2x1 + x2 ≤ 120;
x1 + 1,5x2 ≤ 120;
x1 ≥ 0; x2 ≥ 0;
на множестве решений которой надо найти наибольшее значение целевой функции
|
|
|
F = x1 + x2
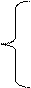
Решение: По условию задачи целевая функция F = x1 + x2 должна иметь наибольшее значение на выпуклом плоском многоугольнике, определенном этими неравенствами. Неравенства определяют часть плоскости, образующей многоугольник решений ОАСВ (рис.14).
Уравнения линий уровня линейной функции F = x1 + x2 имеют вид x1 + x2 = F1, где F1 – значение линейной функции на соответствующей прямой. Прямая x1 + x2 = F1 перпендикулярна вектору F (1, 1). Будем перемещать ее параллельно самой себе в направлении вектора N.
Прямые, проходящие через вершины (30, 60) и (0, 0,), являются опорными для четырехугольника решений, заштрихованного на рис.14. Следовательно, наибольшее значение функции Z принимает при X1 = 30; Х2 = 60 (в вершине С), а наименьшее значение – при х1=х2=0 (в вершине О).
 |
Таким образом, целевая функция имеет наибольшее оптимальное значение при X1 =30 и Х2=60. Оптимальным планом является F max = 30 = 60 = 90.
