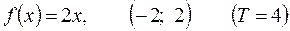
РЕШЕНИЕ:
При решении многих задач физики и математики необходимо осуществить разложение периодической функции с периодом 2π в ряд по тригонометрическим функциям: 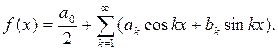
Ряд такого вида называется рядом Фурье, а разложение функции в ряд Фурье составляет задачу гармонического анализа. Важным для понимания данного разложения представляет вопрос: когда ряд Фурье сходится в обычном смысле, т.е. поточечно, и каким образом он описывает функцию f (x)? На так поставленный вопрос дает ответ теорема Дирихле:
Пусть f (x) удовлетворяет в (−π; π) так называемым условиям Дирихле:
a) интервал (−π; π) можно разбить на конечное число интервалов, в которых f (x) непрерывна и монотонна;
b) если x0 является точкой разрыва функции f (x), то существуют односторонние пределы f (x0 + 0) и f (x0 − 0). Тогда ряд Фурье функции f (x) сходится и имеет место равенство
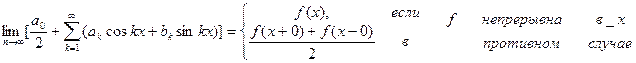 Если раскладываемая в ряд Фурье функция имеет период
Если раскладываемая в ряд Фурье функция имеет период 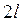 , то ряд Фурье имеет вид
, то ряд Фурье имеет вид
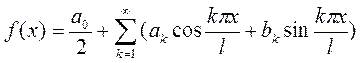 ,
,
при этом коэффициенты вычисляются по формулам:
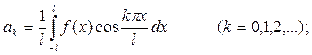
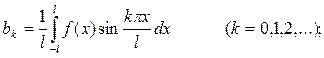
Если раскладываемая в ряд Фурье функция имеет период 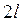 , то ряд Фурье имеет вид
, то ряд Фурье имеет вид
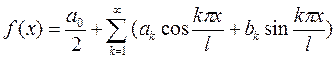 ,
,
при этом коэффициенты вычисляются по формулам:
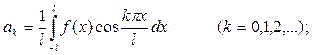
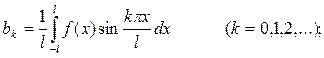
В данном случае имеем: 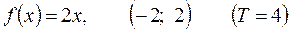
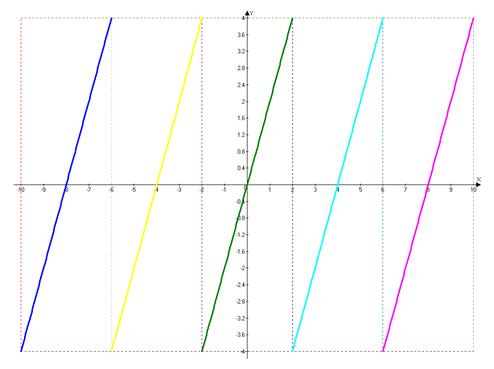
Заданная функция удовлетворяет условиям Дирихле, поэтому разложима в ряд Фурье.
Заданная функция − нечетная 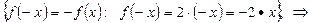
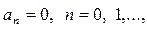 и
и 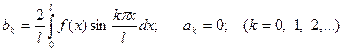 (*)
(*)
При этом ряд Фурье функции f (x) имеет вид:
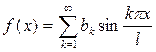 (**)
(**)
По формулам (*) и (**) при 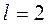 имеем:
имеем: 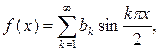
где 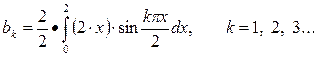
Находим:
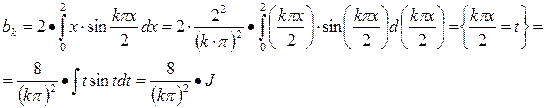
Положим 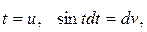 тогда
тогда 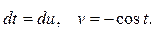
Применяя формулу интегрирования по частям, находим:
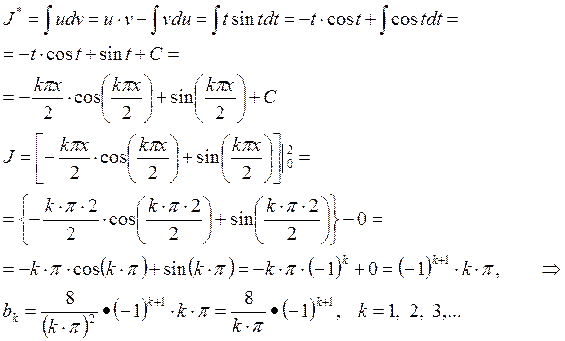
Таким образом, разложение заданной функции в ряд Фурье имеет вид:
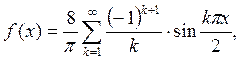
Начертить область на комплексной плоскости по заданным условиям
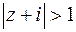 ,
, 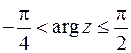 ,
, 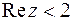 ,
, 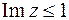 .
.
РЕШЕНИЕ:
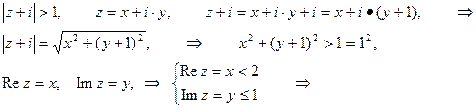
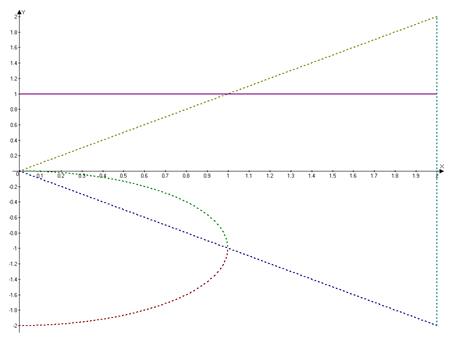
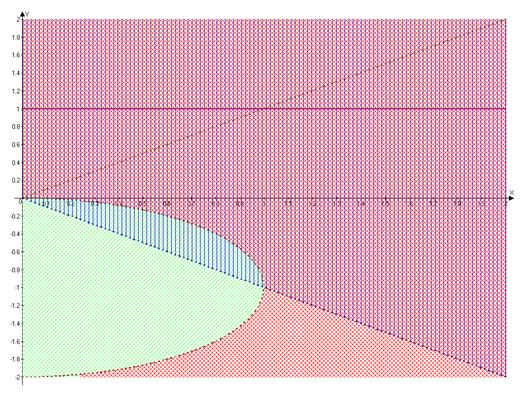
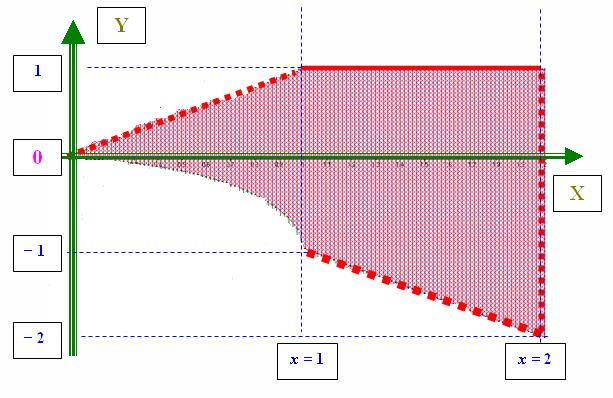
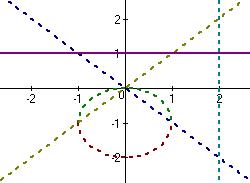 ● заданная область − это внешняя область окружности радиуса
● заданная область − это внешняя область окружности радиуса 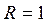 с центром в точке
с центром в точке 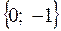 (причем граница окружности не принадлежит заданной области), ограниченная в первом и четвертом квадрантом прямыми:
(причем граница окружности не принадлежит заданной области), ограниченная в первом и четвертом квадрантом прямыми: 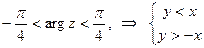
Строим заданную область:
4. Вычислить интеграл по дуге 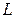 от точки
от точки 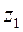 до точки
до точки 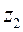
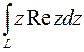 ,
, 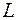 :
: 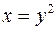 ,
, 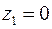 ,
, 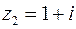
РЕШЕНИЕ:
Имеем:
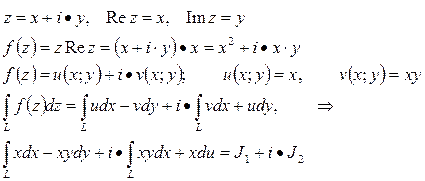
Построим линию, по которой надо вести интегрирование.
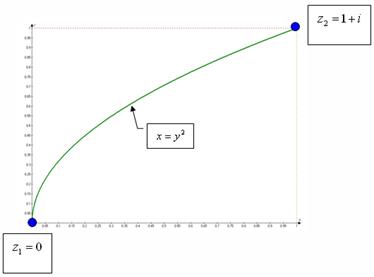 L − отрезок параболы (дуга)
L − отрезок параболы (дуга) 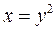
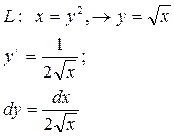
Воспользуемся формулой
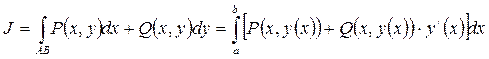
Находим:
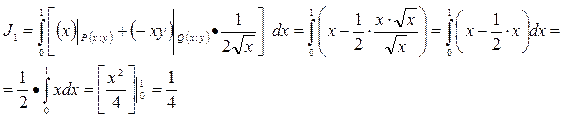
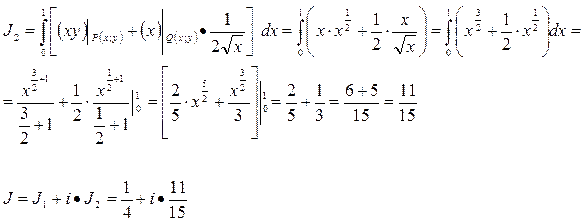
ОТВЕТ: 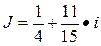
 2020-08-05
2020-08-05 119
119








