СОДЕРЖАНИЕ
ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ_ 2
1. Найти область сходимости степенного ряда_ 3
2. Разложить функцию в ряд Фурье на заданном отрезке (период Т) 6
3. Начертить область на комплексной плоскости по заданным условиям 9
4. Вычислить интеграл по дуге 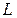 от точки
от точки  до точки
до точки  __ 11
__ 11
5. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом_ 13
ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ
Дистанционное обучение
Дисциплина «Математический анализ». Часть 3
Дополнительные главы. Специальные главы
Вариант № 6
1. Найти область сходимости степенного ряда
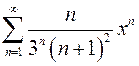
2. Разложить функцию в ряд Фурье на данном отрезке (период Т)
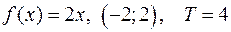
3. Начертить область на комплексной плоскости по данным условиям:
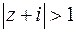 ,
, 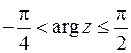 ,
, 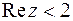 ,
,  .
.
4. Вычислить интеграл по дуге 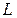 от точки
от точки  до точки
до точки 
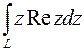 ,
, 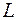 :
:  ,
, 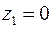 ,
, 
5. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом

Найти область сходимости степенного ряда

РЕШЕНИЕ:
Для определения области сходимости функционального ряда используем признак Даламбера числового ряда, при этом предел вычисляется от выражений функционального ряда взятых по модулю: 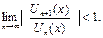
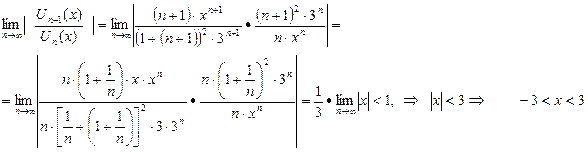
Исследуем ряд на концах найденного интервала (подставляем значения концов интервала в функциональный ряд).
При x = − 3 получаем ряд: 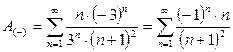
Сходимость знакочередующегося ряда определяется по признаку Лейбница:
1) 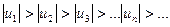 Выполняется. Действительно, имеем[1]:
Выполняется. Действительно, имеем[1]: 
Причем выше показано, что 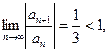
2)  Признаки Лейбница сходимости знакочередующегося ряда выполняются, следовательно, ряд
Признаки Лейбница сходимости знакочередующегося ряда выполняются, следовательно, ряд 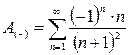 сходится.
сходится.
При x = 3 получаем ряд: 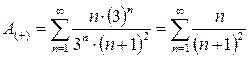
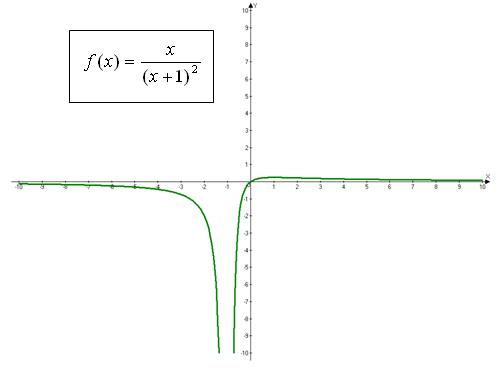
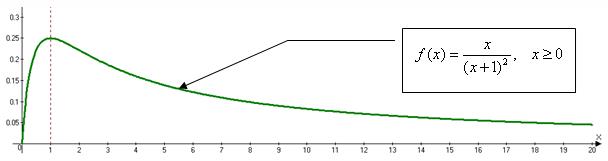
Так как функция 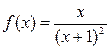 при
при 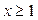 является непрерывной, положительной и монотонно убывающей (см. выше график функции), то для исследования исходного ряда на абсолютную сходимость воспользуемся интегральным признаком Коши:
является непрерывной, положительной и монотонно убывающей (см. выше график функции), то для исследования исходного ряда на абсолютную сходимость воспользуемся интегральным признаком Коши: 
Находим:
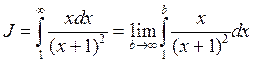
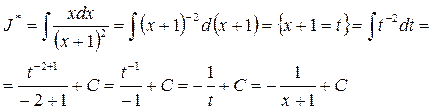
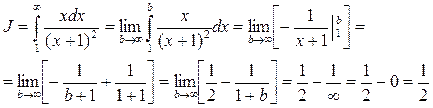
Итак, несобственный интеграл сходится и его значение равно 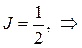 вместе с ним сходится ряд
вместе с ним сходится ряд 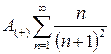
Таким образом, знакочередующийся ряд А(-) сходится абсолютно.
ОТВЕТ:
Область сходимости степенного ряда:

 2020-08-05
2020-08-05 100
100







