1. Изобразим схему с комплексными параметрами, для чего рассчитаем комплексные сопротивления элементов цепи: 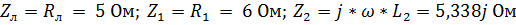 .
.
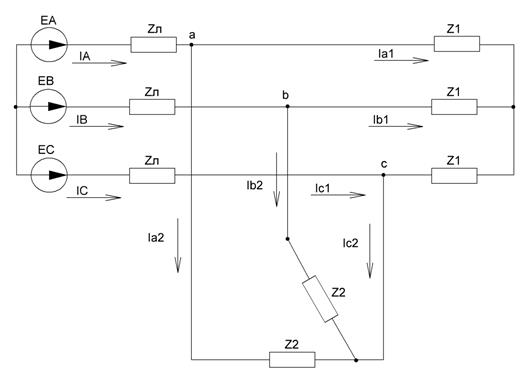
Рисунок 36 - Схема для расчета несимметричного режима с комплексными параметрами
2. Осуществим эквивалентное преобразование соединения «звезды» в «треугольник» для первой нагрузки, для чего рассчитаем необходимые значения сопротивлений ветвей: 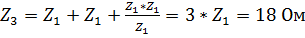 .
.

Рисунок 37 - Схема, полученная после преобразований в пункте 2
3. Преобразуем параллельно соединеные комплексные сопротивления 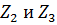 в
в 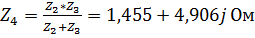 . В результате получим схему, изображенную на рисунке 38.
. В результате получим схему, изображенную на рисунке 38.
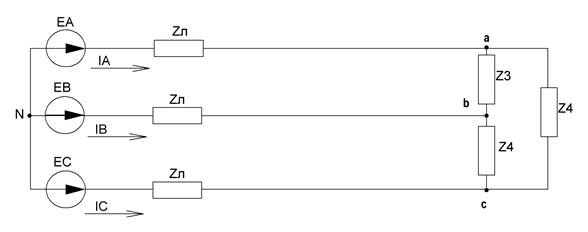
Рисунок 38 – Схема, полученная после преобразований в пункте 3
4. Выполним эквивалентное преобразование «треугольник» - «звезда», рассчитав для этого соответствующие комплексные сопротивления ветвей:
 ,
,
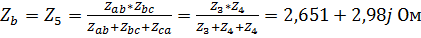 ,
,
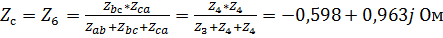 .
.
После данного преобразования получаем схему, изображенную на рисунке 39.

Рисунок 39 – Схема, полученная после преобразований в пункте 4
5. Преобразуем последовательно соединенные комплексные сопротивления каждой фазы в одно сопротивление:
 ,
,
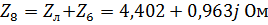 .
.
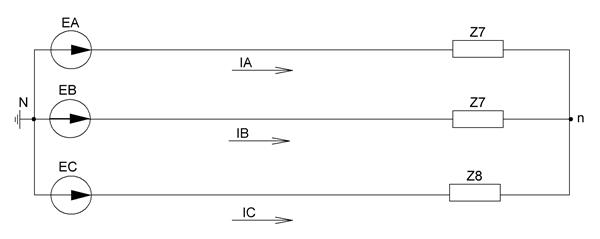
Рисунок 40 – Окончательная схема для расчетов
3.2.3 Определение комплексов действующих значений напряжений и
токов исходной схемы. Расчет показаний ваттметра.
1. Для дальнейших расчетов примем, что точка  заземлена. Так как рассматриваемый режим цепи – несимметричный, то найдем напряжение между нейтральными точками
заземлена. Так как рассматриваемый режим цепи – несимметричный, то найдем напряжение между нейтральными точками 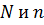 :
:
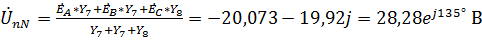 ,
,
где 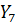 и
и 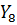 – комплексные проводимости соответствующих ветвей, равные:
– комплексные проводимости соответствующих ветвей, равные:
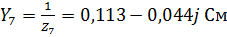 ,
,
 .
.
2. Используя значение 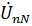 , найдем фазные токи источников:
, найдем фазные токи источников:
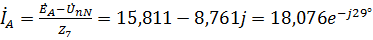 ,
,
 ,
,
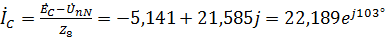 .
.
3. Так как точка  заземлена, то относительно нее
заземлена, то относительно нее 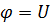 . Тогда найдем потенциалы точек
. Тогда найдем потенциалы точек  относительно
относительно  :
:
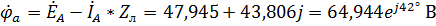 ,
,
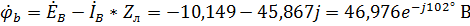 ,
,
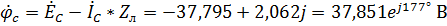 .
.
4. Рассчитаем токи для схемы, представленной на рисунке 36. Линейные токи первой нагрузки будут равны:
 ,
,
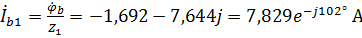 ,
,
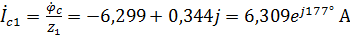 .
.
Рассчитаем линейные токи второй нагрузки:
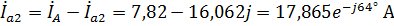 ,
,
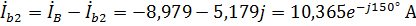 ,
,
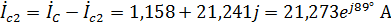 .
.
5. Найдем падения напряжения на каждом комплексном элементе.
Для фазы А:  ,
,
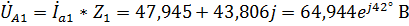 ,
,
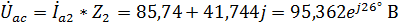 .
.
Для фазы В: 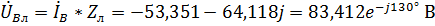 ,
,
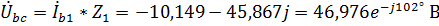 ,
,
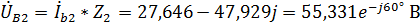 .
.
Для фазы С: 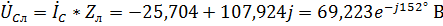 ,
,
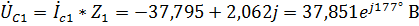 ,
,
Значения линейных напряжений аналогичны значениям, приведенным в симметричном режиме.
6. Рассчитаем показания ваттметра. Они будут определяться следующей формулой:
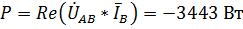 .
.
где  – вещественная часть комплексного числа
– вещественная часть комплексного числа 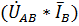 .
.
 2020-08-05
2020-08-05 167
167








