1. Изобразим схему с комплексными параметрами, для чего рассчитаем комплексные сопротивления фаз: 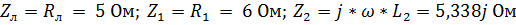 .
.

Рисунок 30 - Схема для расчета симметричного режима с комплексными параметрами
2. Осуществим эквивалентное преобразование соединения «треугольник» в «звезду», для чего рассчитаем необходимые значения сопротивлений ветвей: 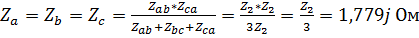 .
.

Рисунок 31 - Эквивалентное преобразование «треугольник» - «звезда»
3. Из полученной в предыдущем пункте схемы видим, что элементы первой и второй нагрузок соединены пофазно параллельно. Значит, можем преобразовать их в одно сопротивление в каждой фазе: 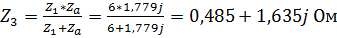 . Тогда получим следующую схему для расчетов:
. Тогда получим следующую схему для расчетов:

Рисунок 32 - Схема с одной нагрузкой, соединенной в «звезду»
4. Так как режим работы цепи – симметричный, то напряжение между нейтральными точками N и n отсутствует. Следовательно, можем считать, что они соединены нейтралью. Тогда из контура с нейтралью и верхней ветвью по второму закону Кирхгофа получаем:
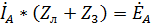 .
.
Тогда сила тока в фазе А равна:
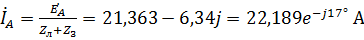 .
.
Так как система симметричная, то, как отмечалось ранее, токи фаз В и С отстают по фазе от тока фазы А на 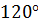 и
и 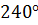 соответственно (или опережают его на
соответственно (или опережают его на 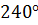 и
и 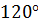 ). Тогда для этих токов получаем:
). Тогда для этих токов получаем: 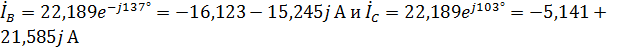 .
.
5. Обратимся к схеме на рисунке 30. Найдем потенциалы точек a, b, c, приняв потенциал точки N равным нулю.
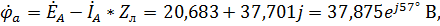


где выражения для потенциалов точек b и c получены путем изменения начальной фазы потенциала точки а на 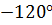 и
и 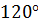 соответственно.
соответственно.
6. Обратимся к схеме на рисунке 31. Потенциалы точек 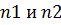 равны нулю, тогда мы можем составить выражения для токов первой нагрузки. Как было указано в пункте 1.4 выражение для тока через потенциалы узлов записывается следующим образом:
равны нулю, тогда мы можем составить выражения для токов первой нагрузки. Как было указано в пункте 1.4 выражение для тока через потенциалы узлов записывается следующим образом:
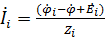 .
.
Тогда составляем следующее выражение:
 .
.
Найдем оставшиеся токи первой нагрузки путем изменения начальной фазы тока  на
на 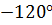 и
и 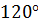 соответственно:
соответственно:
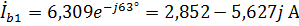 ,
,
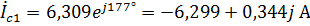 .
.
7. Найдем фазные токи второй нагрузки, соединенной в «треугольник», через потенциалы 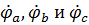 :
:
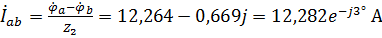 ,
,
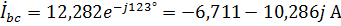 ,
,
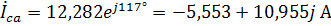 .
.
Здесь значения 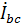 и
и 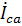 по модулю совпадают с
по модулю совпадают с 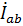 , но по фазе отличаются на
, но по фазе отличаются на 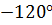 и
и 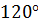 соответственно.
соответственно.
8. Линейные токи второй нагрузки найдем по первому закону Кирхгофа. Для узла а имеем:
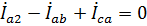 .
.
Тогда искомый ток равен: 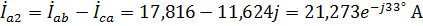 . Токи фаз В и С имеют тот же модуль, но отличаются по фазе на
. Токи фаз В и С имеют тот же модуль, но отличаются по фазе на 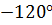 и
и 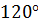 соответственно:
соответственно:
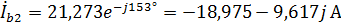 ,
,
 .
.
9. Найдем падения напряжения на каждом комплексном элементе для фазы А:
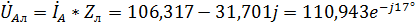 ,
,
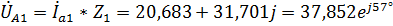 ,
,
 ,
,
где 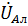 – падение напряжения на элементе
– падение напряжения на элементе  ,
, 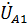 - падение напряжения на элементе
- падение напряжения на элементе 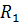 ,
,  - падение напряжения на элементе
- падение напряжения на элементе  .
.
Для фазы В с учетом сдвига фаз на 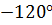 относительно фазы А получаем:
относительно фазы А получаем:
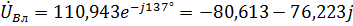 ,
,
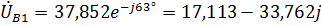 ,
,
 .
.
Для фазы С с учетом сдвига фаз на 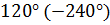 относительно фазы А получаем:
относительно фазы А получаем:
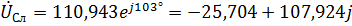 ,
,
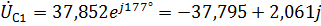 ,
,
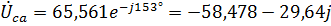 .
.
Линейные напряжения нагрузки равны:
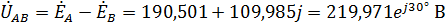 ,
,
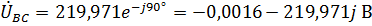 ,
,
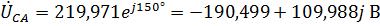 ,
,
где значения  и
и 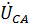 получены путем изменения начальной фазы линейного напряжения
получены путем изменения начальной фазы линейного напряжения 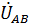 на
на 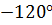 и
и 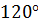 соответственно.
соответственно.
10. Рассчитаем показания ваттметра. Они будут определяться следующей формулой:
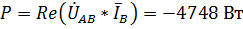 .
.
где  – вещественная часть комплексного числа
– вещественная часть комплексного числа 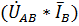 .
.
 2020-08-05
2020-08-05 247
247








