МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПОЛЕЙ
Лабораторная работа № 1
по дисциплинам
«Перспективные методы обработки сигналов РТС»
«Моделирование и оптимизация систем связи»
Цель работы: Изучение методов представления, характеристик и алгоритмов формирования полей сигналов и помех, присущих радиотехническим системам и устройствам.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1. Определения
Полем называется скалярная функция 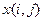 , заданная на плоскости, где
, заданная на плоскости, где 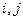 – декартовы координаты. Такими (двумерными) полями являются изображения в телевизионных системах, при этом
– декартовы координаты. Такими (двумерными) полями являются изображения в телевизионных системах, при этом 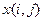 есть интенсивность сигнала (яркость) в точке с координатами
есть интенсивность сигнала (яркость) в точке с координатами  . Поле сигналов может формироваться в результате сканирования диаграммы направленности радиолокационной системы, тогда
. Поле сигналов может формироваться в результате сканирования диаграммы направленности радиолокационной системы, тогда  и
и 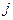 соответствуют угловой координате и дальности до цели. Это примеры скалярных полей. Векторное поле имеет место, если
соответствуют угловой координате и дальности до цели. Это примеры скалярных полей. Векторное поле имеет место, если 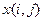 есть вектор с компонентами
есть вектор с компонентами  . В частности, компоненты могут представлять две квадратурные составляющие сигнала.
. В частности, компоненты могут представлять две квадратурные составляющие сигнала.
При цифровой обработке поле обычно задается на совокупности дискретных точек (пикселов) и представляет матрицу с элементами 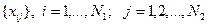 . Эта совокупность точек называется сеткой. Встречаются поля, заданные на пространственной (трехмерной) сетке.
. Эта совокупность точек называется сеткой. Встречаются поля, заданные на пространственной (трехмерной) сетке.
Если 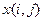 есть случайная функция, то поле является случайным. Для двумерной сетки
есть случайная функция, то поле является случайным. Для двумерной сетки 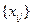 есть совокупность случайных величин, как правило, взаимно зависимых. Простейшие модели случайных полей используют взаимно независимые случайные величины. Такие поля называются полями с независимыми значениями. Они полностью описываются совокупностью (одномерных) функций распределения вероятностей случайных величин в каждой точке поля. В общем случае существуют корреляционные связи между случайными величинами в различных точках.
есть совокупность случайных величин, как правило, взаимно зависимых. Простейшие модели случайных полей используют взаимно независимые случайные величины. Такие поля называются полями с независимыми значениями. Они полностью описываются совокупностью (одномерных) функций распределения вероятностей случайных величин в каждой точке поля. В общем случае существуют корреляционные связи между случайными величинами в различных точках.
Случайное поле называется гауссовским, если оно описывается совместным гауссовским распределением вероятностей для совокупности 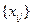 . В противном случае поле являются негауссовским. Поскольку статистическая зависимость в случае гауссовских полей является линейной, то гауссовские поля с зависимыми значениями оказываются коррелированными гауссовскими полями. Гауссовские поля с независимыми значениями оказываются некоррелированными.
. В противном случае поле являются негауссовским. Поскольку статистическая зависимость в случае гауссовских полей является линейной, то гауссовские поля с зависимыми значениями оказываются коррелированными гауссовскими полями. Гауссовские поля с независимыми значениями оказываются некоррелированными.
Для негауссовских полей некоррелированность не означает независимости. Примерами негауссовских полей с независимыми значениями являются поля случайных величин с равномерными распределениями, распределениями Релея, Вейбулла, логарифмическим нормальными и другими.
Если вид и параметры распределений в каждой точке одинаковы, поле называется однородным (пространственно стационарным). Поле может быть изотропным, если его свойства (все характеристики) меняются одинаково в разных направлениях на плоскости. Однородность поля не гарантирует его изотропности, тогда как неоднородное поле, очевидно, неизотропно.
Неоднородность поля помех может быть связана с появлением полезного сигнала в некоторой области изображения.
1.2 Основные характеристики распределений вероятности случайных величин
Обозначим через 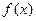 плотность вероятности случайной величины
плотность вероятности случайной величины  , которая имеет область значений
, которая имеет область значений 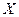 . Если
. Если  имеет размерность, (например, вольты), то
имеет размерность, (например, вольты), то 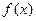 имеет обратную размерность (1/B). Это вытекает из условия нормировки плотности вероятности.
имеет обратную размерность (1/B). Это вытекает из условия нормировки плотности вероятности.
Основными характеристиками одномерных распределений являются статистические моменты (начальные, центральные, абсолютные и др.), кумулянты и квантили.
Начальные моменты  - го порядка
- го порядка 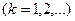 равны
равны 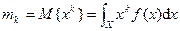 , где
, где  есть оператор математического ожидания. В частности,
есть оператор математического ожидания. В частности, 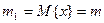 является математическим ожиданием случайной величины
является математическим ожиданием случайной величины  . Второй начальный момент
. Второй начальный момент  имеет размерность
имеет размерность  и называется мощностью
и называется мощностью  случайной величины. В общем случае полное описание одномерной плотности вероятности возможно лишь бесконечной последовательностью начальных моментов.
случайной величины. В общем случае полное описание одномерной плотности вероятности возможно лишь бесконечной последовательностью начальных моментов.
Центральные моменты  - го порядка
- го порядка 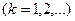 равны
равны  . Очевидно,
. Очевидно,  , а второй центральный момент
, а второй центральный момент  есть дисперсия
есть дисперсия  . Последнее выражение означает, что мощность флуктуаций (случайных изменений) есть полная мощность минус мощность постоянной составляющей.
. Последнее выражение означает, что мощность флуктуаций (случайных изменений) есть полная мощность минус мощность постоянной составляющей.
Для характеристики рассеяния случайной величины относительно ее математического ожидания применяется среднеквадратическое отклонение (СКО) 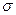 , которое определяется как корень квадратный из дисперсии. Иногда оно называется стандартным отклонением. Отношение
, которое определяется как корень квадратный из дисперсии. Иногда оно называется стандартным отклонением. Отношение 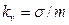 известно как коэффициент вариации.
известно как коэффициент вариации.
Последовательность центральных моментов уже не дает полного описания плотности вероятности, поскольку отсутствует информация о математическом ожидании. Однако эта последовательность полно описывает флуктуации (случайные изменения) величины относительно ее математического ожидания.
Кумулянты  - го порядка
- го порядка 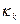 определяются как производные
определяются как производные  - го порядка логарифма характеристической функции
- го порядка логарифма характеристической функции 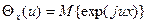 в точке
в точке 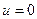 , т. е.
, т. е.  .
.
Характеристическая функция 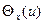 однозначно связана с плотностью вероятностей
однозначно связана с плотностью вероятностей 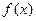 преобразованием Фурье, поэтому начальные моменты и кумулянты однозначно связаны, так что знание всех кумулянтов позволяет определить любой начальный момент и наоборот.
преобразованием Фурье, поэтому начальные моменты и кумулянты однозначно связаны, так что знание всех кумулянтов позволяет определить любой начальный момент и наоборот.
Имеют место следующие соотношения между кумулянтами и моментами:
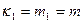 ,
,  ,
,  ,
,
 , и так далее.
, и так далее.
Цепочка кумулянтов бесконечна, также как и цепочка моментов. Единственным исключением является цепочка кумулянтов гауссовской плотности, в которой все кумулянты, кроме первых двух, равны нулю. Заметим, что цепочка моментов в этом случае все равно остается бесконечной. Таким образом, негауссовость распределения проявляется в наличии хотя бы одного ненулевого кумулянта порядка выше второго.
Отметим, что моменты и кумулянты являются размерными величинами. Для описания формы кривой распределения 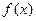 удобно ввести (безразмерные) кумулянтные коэффициенты
удобно ввести (безразмерные) кумулянтные коэффициенты  ,
, 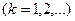 . Очевидно,
. Очевидно,  ,
, 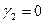 ,
, 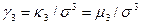 ,
, 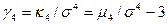 , и так далее. Обычно рассматриваются лишь два старших кумулянтных коэффициента:
, и так далее. Обычно рассматриваются лишь два старших кумулянтных коэффициента: 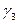 – коэффициент асимметрии,
– коэффициент асимметрии,  – коэффициент эксцесса.
– коэффициент эксцесса.
Для гауссовского распределения остается единственный ненулевой кумулянтный коэффициент  . Знак этого коэффициента определяется знаком математического ожидания. Его обратной величиной является коэффициент вариации. Любое негауссовское распределение характеризуется бесконечной последовательностью кумулянтных коэффициентов, поэтому совокупность
. Знак этого коэффициента определяется знаком математического ожидания. Его обратной величиной является коэффициент вариации. Любое негауссовское распределение характеризуется бесконечной последовательностью кумулянтных коэффициентов, поэтому совокупность  дает лишь частичную характеристику формы распределения.
дает лишь частичную характеристику формы распределения.
При  плотность вероятности имеет более «тяжелый» правый хвост, а при
плотность вероятности имеет более «тяжелый» правый хвост, а при 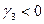 – более «тяжелый» левый хвост. Положительные значения коэффициента эксцесса отражают более острую вершину плотности в окрестности максимального значения (моды) по сравнению с гауссовской, а отрицательные – более плоскую.
– более «тяжелый» левый хвост. Положительные значения коэффициента эксцесса отражают более острую вершину плотности в окрестности максимального значения (моды) по сравнению с гауссовской, а отрицательные – более плоскую.
Моменты и кумулянты распределений не могут принимать произвольные значения. Математическое ожидание имеет область допустимых значений, которая совпадает с областью возможных значений самой случайной величины, а дисперсия всегда положительна: 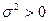 .
.
Существуют известные соотношения между  ,
, 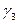 и
и  :
:  ,
,  , которые обеспечивают неотрицательность плотности вероятности. Для случайных величин, принимающих неотрицательные значения, таких как амплитуда, мощность, выполняется неравенство
, которые обеспечивают неотрицательность плотности вероятности. Для случайных величин, принимающих неотрицательные значения, таких как амплитуда, мощность, выполняется неравенство 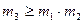 , отсюда следует
, отсюда следует  .
.
Иногда применяются абсолютные моменты  - го порядка
- го порядка 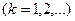 , начальные
, начальные 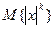 и центральные
и центральные 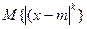 . Абсолютный центральный момент первого порядка
. Абсолютный центральный момент первого порядка  используется для характеристики рассеяния и называется средним отклонением. Отметим, что цепочка абсолютных начальных моментов уже не является полной характеристикой плотности ввиду потери информации о знаках в четных степенях. Это тем более относится к цепочке абсолютных центральных моментов.
используется для характеристики рассеяния и называется средним отклонением. Отметим, что цепочка абсолютных начальных моментов уже не является полной характеристикой плотности ввиду потери информации о знаках в четных степенях. Это тем более относится к цепочке абсолютных центральных моментов.
В связи с «проблемой моментов» возникают следующие два вопроса:
1. При каких условиях произвольная последовательность чисел представляет моменты (кумулянты) некоторой случайной величины?
2. При каких условиях последовательность моментов (кумулянтов) единственным образом определяют распределение случайной величины?
Эти условия связаны с областью значений и типом случайной величины (дискретная, непрерывная) и здесь не рассматриваются.
Квантилем, соответствующим вероятности  , т. е.
, т. е.  - квантилем, называется значение
- квантилем, называется значение  , для которого вероятность
, для которого вероятность  . Процентной точкой
. Процентной точкой  будем называть квантиль
будем называть квантиль  . В этом случае вероятность равна
. В этом случае вероятность равна  или
или  процентов. Медиана распределения
процентов. Медиана распределения  есть 0,5-квантиль, которая совпадает с 50-процентной точкой. Она является характеристикой положения наряду с математическим ожиданием. Мода распределения
есть 0,5-квантиль, которая совпадает с 50-процентной точкой. Она является характеристикой положения наряду с математическим ожиданием. Мода распределения 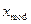 есть аргумент максимального значения плотности вероятности и также характеризует положение плотности. Если мода единственна, то распределение называют унимодальным.
есть аргумент максимального значения плотности вероятности и также характеризует положение плотности. Если мода единственна, то распределение называют унимодальным.
Существуют и другие характеристики одномерного распределения, например, факториальные моменты. Следует подчеркнуть, что в общем случае никакая конечная совокупность числовых характеристик не дает полного описания плотности вероятности. Однако имеются модельные распределения, для характеристики которых достаточно знать конечное число параметров.
1.3 Основные модельные распределения вероятности
Равномерное распределение  задается на отрезке
задается на отрезке  , где
, где  и имеет на этом отрезке постоянное значение плотности вероятности, равное
и имеет на этом отрезке постоянное значение плотности вероятности, равное 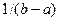 . Статистические моменты даются формулой
. Статистические моменты даются формулой 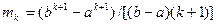 ,
, 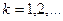 . Если
. Если 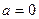 ,
, 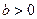 , то
, то 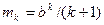 . В частности,
. В частности,  ,
,  , а дисперсия
, а дисперсия 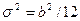 . Кумулянтные коэффициенты
. Кумулянтные коэффициенты  ,
, 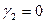 ,
,  отражают симметрию и плосковершинность кривой плотности вероятности (по отношению к гауссовской плотности). Коэффициент вариации равен
отражают симметрию и плосковершинность кривой плотности вероятности (по отношению к гауссовской плотности). Коэффициент вариации равен 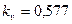 .
.
Нормальное или гауссовское распределение 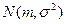 имеет плотность вероятности
имеет плотность вероятности  , где математическое ожидание
, где математическое ожидание 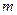 и дисперсия
и дисперсия  являются параметрами распределения. Все кумулянтные коэффициенты, начиная с третьего, равны нулю. Среднее отклонение равно
являются параметрами распределения. Все кумулянтные коэффициенты, начиная с третьего, равны нулю. Среднее отклонение равно  . Помимо отмеченного выше свойства кумулянтов, нормальное распределение играет фундаментальную роль в теории распределений. Это объясняется тем, что распределение суммы случайных величин при широких предположениях относительно свойств каждой из величин с ростом числа слагаемых стремится к гауссовскому распределению (соответствующие условия являются содержанием центральной предельной теоремы).
. Помимо отмеченного выше свойства кумулянтов, нормальное распределение играет фундаментальную роль в теории распределений. Это объясняется тем, что распределение суммы случайных величин при широких предположениях относительно свойств каждой из величин с ростом числа слагаемых стремится к гауссовскому распределению (соответствующие условия являются содержанием центральной предельной теоремы).
Отметим, что коэффициент вариации обращается в бесконечность в случае 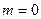 . Часто удобной величиной является кумулянтный коэффициент
. Часто удобной величиной является кумулянтный коэффициент  , который может принимать положительные и отрицательные значения.
, который может принимать положительные и отрицательные значения.
Для симметричных унимодальных распределений математическое ожидание совпадает с медианой и с модой. Следующие распределения описывают неотрицательные случайные величины.
Распределение Вейбулла 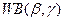 с параметром масштаба
с параметром масштаба  и параметром формы
и параметром формы 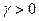 имеет плотность вероятности
имеет плотность вероятности  ,
,  . Начальные моменты распределения определяются выражением
. Начальные моменты распределения определяются выражением 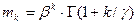 ,
, 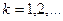 , где
, где 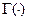 – гамма-функция,
– гамма-функция,  ,
,  . Для целых аргументов
. Для целых аргументов 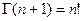 .
.
При 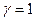 распределение Вейбулла переходит в экспоненциальное распределение
распределение Вейбулла переходит в экспоненциальное распределение  с плотностью вероятности
с плотностью вероятности  . У этого распределения математическое ожидание и дисперсия равны соответственно
. У этого распределения математическое ожидание и дисперсия равны соответственно 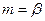 и
и  . Коэффициент вариации равен единице, коэффициенты асимметрии и эксцесса равны
. Коэффициент вариации равен единице, коэффициенты асимметрии и эксцесса равны 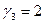 ,
,  . Иногда при сравнении распределений удобно пользоваться отношением
. Иногда при сравнении распределений удобно пользоваться отношением 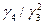 , которое в данном случае равно 1,5.
, которое в данном случае равно 1,5.
Плотности вероятности для распределений Вейбулла являются несимметричными, поэтому математическое ожидание отличается от моды и от медианы. Характерным является отношение математического ожидания к медиане  . Для экспоненциального распределения
. Для экспоненциального распределения  , а отношение
, а отношение  .
.
Для распределений Вейбулла с 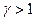 при увеличении значения
при увеличении значения 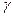 асимметрия и эксцесс уменьшаются, математическое ожидание
асимметрия и эксцесс уменьшаются, математическое ожидание  и медиана
и медиана  сближаются и стремятся к
сближаются и стремятся к 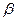 .
.
При  распределение переходит в распределение Релея
распределение переходит в распределение Релея 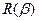
 , у которого математическое ожидание и второй момент равны
, у которого математическое ожидание и второй момент равны  ,
,  . Дисперсия распределения
. Дисперсия распределения 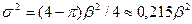 , т. е.
, т. е. 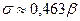 , а значение коэффициента вариации
, а значение коэффициента вариации 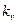 приблизительно равно
приблизительно равно 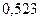 . Медиана релеевского распределения
. Медиана релеевского распределения  , а отношение математического ожидания к медиане
, а отношение математического ожидания к медиане  . Коэффициенты асимметрии и эксцесса в первом приближении равны
. Коэффициенты асимметрии и эксцесса в первом приближении равны 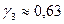 ,
,  , т. е. кривая плотности релеевского распределения более острая по сравнению с плотностью нормального распределения
, т. е. кривая плотности релеевского распределения более острая по сравнению с плотностью нормального распределения 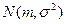 .
.
В первом приближении для всех распределений Вейбулла с 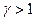 можно считать
можно считать  .
.
Логарифмическое нормальное распределение 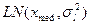 имеет плотность (для неотрицательных значений случайной величины)
имеет плотность (для неотрицательных значений случайной величины)  ,
,  , где
, где  есть дисперсия величины
есть дисперсия величины 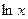 . Математическое ожидание и дисперсия равны
. Математическое ожидание и дисперсия равны 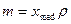 ,
, 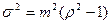 , где отношение математического ожидания к медиане
, где отношение математического ожидания к медиане  . Начальные моменты логарифмического нормального распределения равны
. Начальные моменты логарифмического нормального распределения равны  . Распределение является двухпараметрическим. Медиана является параметром масштаба, а в качестве параметра формы можно выбрать
. Распределение является двухпараметрическим. Медиана является параметром масштаба, а в качестве параметра формы можно выбрать 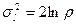 , отношение математического ожидания к медиане
, отношение математического ожидания к медиане 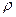 , или квадрат коэффициента вариации
, или квадрат коэффициента вариации 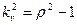 . Если вместо параметров
. Если вместо параметров 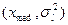 использовать
использовать  , то плотность записывается в виде
, то плотность записывается в виде 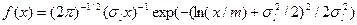 .
.
Любой кумулянтный коэффициент логарифмического нормального распределения выражается через отношение 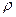 , либо через коэффициент вариации
, либо через коэффициент вариации 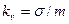 :
:  ,
,  . Кумулянтные коэффициенты всегда положительны, поскольку
. Кумулянтные коэффициенты всегда положительны, поскольку  . Часто вместо величины
. Часто вместо величины  используется
используется  , которая выражается в децибелах, т. е.
, которая выражается в децибелах, т. е. 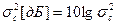 . В частности,
. В частности, 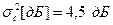 , соответствует
, соответствует  ,
, 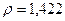 ,
, 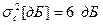 соответствует
соответствует 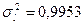 ,
,  . В первом приближении для плотностей логарифмического нормального распределения справедливо соотношение
. В первом приближении для плотностей логарифмического нормального распределения справедливо соотношение  .
.
Гамма-распределение  описывается плотностью вероятности (для неотрицательной случайной величины)
описывается плотностью вероятности (для неотрицательной случайной величины) 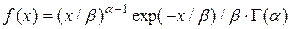 ,
,  , где параметр формы
, где параметр формы 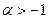 , а
, а  – параметр масштаба. Кумулянты распределения
– параметр масштаба. Кумулянты распределения 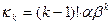 , откуда математическое ожидание и дисперсия равны
, откуда математическое ожидание и дисперсия равны  ,
, 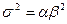 . Кумулянтные коэффициенты равны
. Кумулянтные коэффициенты равны  . При
. При 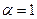 распределение сводится к экспоненциальному, которое является общим для семейств гамма-распределения и распределения Вейбулла. С увеличением значений параметра формы высшие кумулянтные коэффициенты убывают, т. е. форма плотности вероятности стремится к гауссовской.
распределение сводится к экспоненциальному, которое является общим для семейств гамма-распределения и распределения Вейбулла. С увеличением значений параметра формы высшие кумулянтные коэффициенты убывают, т. е. форма плотности вероятности стремится к гауссовской.
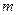 -распределение Накагами
-распределение Накагами  имеет плотность вероятности
имеет плотность вероятности  для
для  . Распределение хорошо моделирует амплитудные флуктуации и замирания сигналов в различных средах. Параметр формы
. Распределение хорошо моделирует амплитудные флуктуации и замирания сигналов в различных средах. Параметр формы 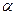 иногда обозначается буквой
иногда обозначается буквой 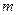 , что и определяет связь с названием распределения. При
, что и определяет связь с названием распределения. При 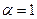 получается распределение Релея, случай
получается распределение Релея, случай  описывает сильные (глубокие) замирания, а
описывает сильные (глубокие) замирания, а 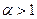 характерен для слабых замираний.
характерен для слабых замираний.
Моменты определяются по формуле  . В ряде случаев в качестве параметра масштаба используется второй момент
. В ряде случаев в качестве параметра масштаба используется второй момент  , отсюда
, отсюда 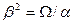 . Случайная величина с
. Случайная величина с 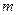 - распределением
- распределением  после возведения в квадрат приобретает гамма-распределение
после возведения в квадрат приобретает гамма-распределение 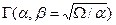 .
.
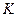 - распределение
- распределение  имеет плотность вероятности
имеет плотность вероятности 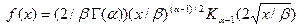 при
при  и
и 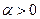 . Здесь
. Здесь  – представляет модифицированную функцию Бесселя второго рода*). Иногда в качестве параметра формы вводится величина
– представляет модифицированную функцию Бесселя второго рода*). Иногда в качестве параметра формы вводится величина 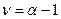 .
.
*) Справочник по специальным функциям: Под ред. М. Абрамовица, И. Стиган. Пер. с англ. – М.: Наука, 1979.
Начальные моменты вычисляются по формуле 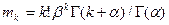 . Распределение можно получить путем умножения двух случайных величин с распределениями
. Распределение можно получить путем умножения двух случайных величин с распределениями  и
и 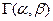 . Квадрат коэффициента вариации распределения
. Квадрат коэффициента вариации распределения  всегда больше единицы.
всегда больше единицы.
Распределение хорошо моделирует флуктуации интенсивности и эффекты затенения лучей при распространении вдоль неровной земной или морской поверхности.
При  распределение совпадает с распределением Вейбулла с параметром формы
распределение совпадает с распределением Вейбулла с параметром формы 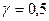 , вчетверо меньшим параметром масштаба
, вчетверо меньшим параметром масштаба  , а при
, а при  распределение стремится к экспоненциальному распределению
распределение стремится к экспоненциальному распределению 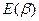 .
.
Другая форма 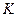 - распределения описывает амплитудные флуктуации. Величина
- распределения описывает амплитудные флуктуации. Величина 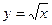 имеет плотность вероятности
имеет плотность вероятности 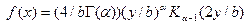 , где
, где  . Теперь четные начальные моменты
. Теперь четные начальные моменты 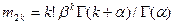 . При
. При  это распределение стремится к релеевскому распределению
это распределение стремится к релеевскому распределению 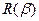 .
.
Рассмотренные одномерные распределения, конечно, не исчерпывают все применяемые модельные распределения. Можно указать более общие классы многопараметрических распределений, однако увеличение числа параметров резко усложняет теоретический анализ и практическое моделирование соответствующих полей. Другое направление развития моделей представляют случайные поля с зависимыми значениями, в частности, гауссовские коррелированные поля.
1.4 Моделирование случайных полей и выборочная оценка параметров распределений
В данной работе исследуются случайные поля с независимыми значениями. Формирование случайных чисел осуществляется на сетке (совокупности точек) размером  элементов. В программе предусмотрена визуализация формируемых случайных полей в двух окнах, что позволяет сравнивать различные распределения.
элементов. В программе предусмотрена визуализация формируемых случайных полей в двух окнах, что позволяет сравнивать различные распределения.
Отметим, что случайной величиной является яркость, которая связана с интенсивностью поля в данной точке. Разные цвета используются для лучшего различения градаций яркости.
Случайные числа с равномерным распределением получаются стандартным конгруэнтным методом (конгруэнтность есть равенство двух чисел по модулю 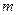 , например,
, например,  .
.
Рекуррентный алгоритм формирования случайного числа имеет вид  , где заданы константы
, где заданы константы  ,
, 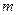 и начальное значение
и начальное значение  . При этом случайные числа
. При этом случайные числа 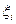 распределены равномерно в интервале
распределены равномерно в интервале  . Для получения требуемого интервала
. Для получения требуемого интервала  следует умножить число
следует умножить число 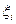 на
на 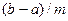 , а затем добавить
, а затем добавить  .
.
Если  и
и 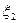 – два независимых случайных числа с равномерным распределением на интервале
– два независимых случайных числа с равномерным распределением на интервале  . Тогда два независимых случайных числа с нормальным распределением формируются по формулам:
. Тогда два независимых случайных числа с нормальным распределением формируются по формулам: 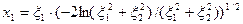 ,
, 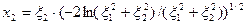 .
.
Случайные числа с распределением Вейбулла  получаются из равномерно распределенных на интервале
получаются из равномерно распределенных на интервале  путем нелинейного преобразования
путем нелинейного преобразования  . В частности, при
. В частности, при 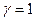 получаются числа с экспоненциальным распределением.
получаются числа с экспоненциальным распределением.
Формирование случайных чисел с логарифмическим нормальным распределением  легко осуществить, имея случайные числа с нормальным распределением. Если
легко осуществить, имея случайные числа с нормальным распределением. Если  , где
, где 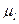 и
и 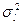 – математическое ожидание и дисперсия исходного нормального распределения, то
– математическое ожидание и дисперсия исходного нормального распределения, то  распределено логарифмически нормально с параметрами
распределено логарифмически нормально с параметрами  и
и 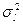 . Если требуется получить заданное математическое ожидание
. Если требуется получить заданное математическое ожидание 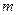 для логарифмического нормального распределения, то надо выбрать
для логарифмического нормального распределения, то надо выбрать  . Если
. Если  имеет стандартное нормальное распределение
имеет стандартное нормальное распределение  , то
, то  имеет логарифмическое нормальное распределение с параметрами
имеет логарифмическое нормальное распределение с параметрами  ,
,  или
или 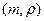 , где
, где 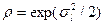 . Часто удобно использовать параметры
. Часто удобно использовать параметры  , где коэффициент вариации
, где коэффициент вариации  является параметром формы. Последний вариант применен в программе моделирования.
является параметром формы. Последний вариант применен в программе моделирования.
Случайное число с гамма-распределением  моделируется в частных случаях целых значений параметра формы
моделируется в частных случаях целых значений параметра формы 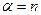 . В этих случаях оно может быть получено суммированием
. В этих случаях оно может быть получено суммированием  независимых экспоненциально распределенных чисел с распределением
независимых экспоненциально распределенных чисел с распределением 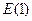 с последующим умножением на
с последующим умножением на  . Параметр
. Параметр 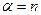 в этом случае равен числу суммируемых случайных чисел.
в этом случае равен числу суммируемых случайных чисел.
Имея выборку из 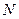 случайных чисел
случайных чисел  , можно вычислить выборочные начальные моменты
, можно вычислить выборочные начальные моменты  , которые являются оценками статистических моментов
, которые являются оценками статистических моментов  . В отличие от статистических моментов выборочные моменты являются случайными величинами и сами характеризуются математическими ожиданиями, дисперсиями и высшими моментами. Известно, что выборочные моменты являются состоятельными оценками для
. В отличие от статистических моментов выборочные моменты являются случайными величинами и сами характеризуются математическими ожиданиями, дисперсиями и высшими моментами. Известно, что выборочные моменты являются состоятельными оценками для 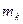 , т.е. для любого малого
, т.е. для любого малого  вероятность
вероятность  стремится к 1 с ростом
стремится к 1 с ростом 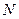 . В этом смысле (т. е. с вероятностью единица) выборочные характеристики сходятся к теоретическим значениям, однако скорость сходимости отличается для разных распределений и различных характеристик.
. В этом смысле (т. е. с вероятностью единица) выборочные характеристики сходятся к теоретическим значениям, однако скорость сходимости отличается для разных распределений и различных характеристик.
Программное обеспечение позволяет получать выборочные оценки математического ожидания, дисперсии, коэффициентов асимметрии и эксцесса, которые вычисляются по следующим формулам:  ,
,  ,
, 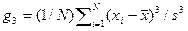 ,
,  .
.
Задание размера выборки N осуществляется вводом количества строк анализируемого поля (каждая строка содержит 256 выборок) в соответствующем окне изображения, т. е.  , где
, где  – количество первых строк поля.
– количество первых строк поля.
2. ОПИСАНИЕ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
ДЛЯ СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
2.1 Состав программного обеспечения
Программное обеспечение включает четыре блока программ, объединенных единой оболочкой:
1. Моделирование случайных полей.
2. Оценка характеристик и параметров.
3. Моделирование полезных сигналов.
4. Обнаружение сигналов.
Переход к тому или иному блоку программ осуществляется выбором соответствующего режима в главном меню (верхняя строка) с помощью клавиш-стрелок и [Enter]:
1. "Распределение" 2. "Оценка" 3. "Сигнал" 4. "Порог"
Режим "Выход" обеспечивает выход из программных блоков.
 2020-09-24
2020-09-24 558
558







