Шифры полиалфавитной подстановки

 

Слабая криптостойкость моноалфавитных подстановок преодолевается с применением подстановок многоалфавитных (полиалфавитных). Многоалфавитное шифрование (многоалфавитная замена) заключается в том, что для шифрования последовательных символов исходного текста используются одноалфавитные методы с различными ключами или, иными словами, – свои специальные алфавиты.

Например, первый символ заменяется по методу Цезаря со смещением 18, второй – со смещением 12 и т.д. до конца ключа, задающего переход к новому смещению. Затем процедура продолжается периодически. Более общей является ситуация, когда используется не шифр Цезаря, а последовательность произвольных подстановок, соответствующих одноалфавитным методам.

Шифр Виженера. Самым широко известным и одновременно самым простым алгоритмом такого рода является шифр Виженера (Vigenere). Этот шифр базируется на наборе правил моноалфавитной подстановки, представленных для латинского алфавита из 26 букв шифрами Цезаря со сдвигом от 0 до 25. Каждый из таких шифров можно обозначить ключевой буквой, являющейся буквой шифрованного текста, соответствующей букве a открытого текста. Например, шифр Цезаря, для которого смещение равно 3, обозначается ключевой буквой d. Для полного алфавита русского языка могут использоваться 32 шифра Цезаря со сдвигом от 0 до 32.

Для облегчения понимания и применения этой схемы была предложена матрица, названная “табло Виженера” (рис. 2.21 и 2.22). Все 26 (для русского алфавита – 33, а в данном случае – 32) шифров располагаются по горизонтали, и каждому из шифров соответствует своя ключевая буква, представленная в крайнем столбце слева. Алфавит, соответствующий буквам открытого текста, находится в первой сверху строке таблицы. Процесс шифрования прост – необходимо по букве Х, задаваемой ключом, и букве открытого текста У найти букву шифрованного текста, которая находится на пересечении строки Х и столбца У. В данном случае такой буквой является буква V.

Рис. 2.21. Современное табло Виженера для латинского алфавита

Чтобы зашифровать сообщение, нужен ключ, имеющий ту же длину, что и само сообщение. Обычно ключ представляет собой повторяющееся нужное число раз ключевое слово, чтобы получить строку подходящей длины. Например, если ключевым словом является deceptive / обманчивый /, сообщение «we are discovered save yourself» / мы раскрыты, спасайте себя / шифруется следующим образом.

Расшифровать текст также просто – буква ключа определяет строку, буква шифрованного текста, находящаяся в этой строке, определяет столбец, и в этом столбце в первой строке таблицы будет находиться соответствующая буква открытого текста.

Рис. 2.22. Таблица Виженера для русского алфавита

Рассмотрим еще один пример получения шифротекста с помощью таблицы Виженера. Пусть выбрано ключевое слово АМБРОЗИЯ. Необходимо зашифровать сообщение на русском языке ПРИЛЕТАЮ СЕДЬМОГО.

Выпишем исходное сообщение в строку и запишем под ним ключевое слово с повторением. В третью строку будем выписывать буквы шифротекста, определяемые из таблицы Виженера.

 

 

Преимущество этого шифра заключается в том, что для представления одной и той же буквы открытого текста в шифрованном тексте имеется много различных вариантов – по одному на каждую из неповторяющихся букв ключевого слова. Таким образом, скрывается информация, характеризующая частотность употребления букв. Но и с помощью данного метода все же не удается полностью скрыть влияние структуры открытого текста на структуру шифрованного.

Можно отметить два предложения по усовершенствованию шифра Виженера. Инженером компании AT&T Гилбертом Вернамом (Gilbert Vernam) в 1918 г. было предложено выбирать ключевое слово, по длине равное длине открытого текста, но отличающегося от открытого текста по статистическим показателям (то есть в общем случае речь шла о фрагменте некоторого текста). Кроме того, система Вернама оперирует не буквами, а двоичными числами[4]. Кратко ее можно выразить формулой:

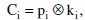
где р_i – i-я двоичная цифра открытого текста; k_i – i-я двоичная цифра ключа; C_i – i-я двоичная цифра шифрованного текста; ⓧ – операция XOR (исключающее “ИЛИ”)[5].

Таким образом, шифрованный текст генерируется путем побитового выполнения операции XOR для открытого текста и ключа. Благодаря свойствам этой операции для расшифровки достаточно выполнить подобную операцию:

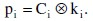
Сутью этой технологии является способ выбора ключа. Г.Вернам предложил использовать закольцованную ленту, что означает циклическое повторение ключевого слова, так что его система на самом деле предполагала работу хоть и с очень длинным, но все же повторяющимся ключом. Несмотря на то, что такая схема в силу очень большой длины ключа значительно усложняет задачу криптоанализа, схему, тем не менее, можно взломать, имея в распоряжении достаточно длинный фрагмент шифрованного текста, известные или вероятно известные фрагменты открытого текста либо и то, и другое сразу.

Офицер армейского корпуса связи Джозеф Моборн (Joseph Mauborgne) предложил такие улучшения схемы шифрования Вернама, которые сделали эту схему исключительно надежной. Моборн предложил отказаться от повторений, а случайным образом генерировать ключ, по длине равный длине сообщения. Такая схема, получившая название ленты однократного использования (или схемы с одноразовым блокнотом), взлому не поддается. В результате ее применения на выходе получается случайная последовательность, не имеющая статистической взаимосвязи с открытом текстом. Поскольку в этом случае шифрованный текст не дает никакой информации об открытом тексте, нет способа и взломать код.

Сложность практического применения этого метода заключается в том, что и отправитель, и получатель должны располагать одним и тем же случайным ключом и иметь возможность защитить его от посторонних. Поэтому, несмотря на все преимущества шифра Вернама-Моборна перед другими шифрами, на практике к нему прибегают редко.

 

Шифр “двойной квадрат” Уитстона. В 1854 г. англичанин Чарльз Уитстон разработал новый метод шифрования биграммами, который называют “двойным квадратом”. Свое название этот шифр получил по аналогии с полибианским квадратом, изобретенным в древнем мире. Шифр Уитстона открыл новый этап в истории развития криптографии. В отличие от полибианского шифр «двойной квадрат» использует сразу две таблицы, размещенные по одной горизонтали, а шифрование идет биграммами, как в шифре Плейфейера. Эти не столь сложные модификации привели к появлению на свет качественно новой криптографической системы ручного шифрования. Шифр «двойной квадрат» оказался очень надежным и удобным и применялся Германией даже в годы Второй мировой войны.

Поясним процедуру шифрования этим шифром на примере. Пусть имеются две таблицы со случайно расположенными в них буквами русского алфавита (рис. 2.23)[6]. Перед шифрованием исходное сообщение разбивают на биграммы. Каждая биграмма шифруется отдельно. Первую букву биграммы находят в левой таблице, а вторую букву – в правой таблице. Затем мысленно строят прямоугольник так, чтобы буквы биграммы лежали в его противоположных вершинах. Другие две вершины этого прямоугольника дают буквы биграммы шифротекста. Первый символ шифрованной пары должен лежать в одной строке с первым символом исходной.

Ж

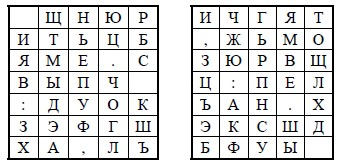
Рис. 2.23. Две таблицы со случайно расположенными символами русского алфавита для шифра «двойной квадрат»

 

Предположим, что шифруется биграмма исходного текста ИЛ. Буква И находится в столбце 1 и строке 2 левой таблицы. Буква Л находится в столбце 5 и строке 4 правой таблицы. Это означает, что прямоугольник образован строками 2 и 4, а также столбцами 1 левой таблицы и 5 правой таблицы. Следовательно, в биграмму шифротекста входят буква О, расположенная в столбце 5 и строке 2 правой таблицы, и буква В, расположенная в столбце 1 и строке 4 левой таблицы, т.е. получаем биграмму шифротекста ОВ.

Если обе буквы биграммы сообщения лежат в одной строке, то и буквы шифротекста берут из этой же строки. Пусть первый символ имеет позицию (s, c) в левой таблице. Тогда он заменяется тем символом правой таблицы, какой там стоит на позиции (s, c). Пусть второй символ имеет позицию (s2, c2) в правой таблице. Тогда он заменяется тем символом левой таблицы, какой там стоит на позиции (s2, c2).

Поэтому биграмма сообщения ТО превращается в биграмму шифротекста ЖБ. Аналогичным образом шифруются все биграммы сообщения:

ЖБ

Шифрование методом «двойного квадрата» дает весьма устойчивый к вскрытию и простой в применении шифр. Взламывание шифротекста «двойного квадрата» требует больших усилий, при этом длина сообщения должна быть не менее тридцати строк.

Расшифровывание требует тех же действий, что и шифрование, только в обратном порядке. Обратный порядок означает, между прочим, что первая буква биграммы шифротекста выбирается в правой таблице, а вторая – в левой.

Две таблицы со случайно расположенными в них буквами естественного алфавита можно рассматривать как два секретных ключа. В то же время их можно рассматривать как форму представления двух специальных алфавитов для записи шифротекстов. Это доказывает, что шифр “двойной квадрат” Уитстона является частным случаем много алфавитных шифров.