Шифры моноалфавитной подстановки

 

Шифры моноалфавитной (одноалфавитной) подстановки относятся к категории шифров замены (подстановки). Другое их название – шифры простой замены. В шифре простой замены каждый символ исходного текста заменяется по определенному правилу символами одного и того же специального алфавита шифротекста на всем протяжении текста.

Шифр Цезаря.

Историческим примером шифра замены является шифр Цезаря (I век до н.э.), описанный историком Древнего Рима Светонием. Гай Юлий Цезарь использовал в своей переписке шифр собственного изобретения. Применительно к современному русскому языку он состоял в следующем. Выписывался алфавит: А, Б, В, Г, Д, Е,...; затем под ним выписывался тот же алфавит, но со сдвигом на 3 буквы влево (табл. 2.5). Можно сказать, что осуществился переход к специальному алфавиту, на котором будет записываться шифротекст.

 

Таблица 2.5

 

Подстановки по шифру Цезаря для алфавита русского языка

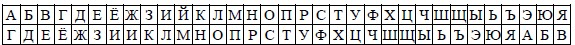
Обратите внимание на то, что алфавит считается “циклическим”, поэтому после Я идет А. При шифровке буква А заменялась буквой Г, Б заменялась на Д, В – на Е и т.д. Так, например, слово “РИМ” превращалось в слово “УЛП”. Получатель сообщения “УЛП” искал эти буквы в нижней строке и по буквам над ними восстанавливал исходное слово “РИМ”. Ключом в шифре Цезаря является величина сдвига 3 алфавита открытого текста. Преемник Юлия Цезаря – цезарь Август – использовал тот же шифр, но с ключом-сдвигом 4. Слово “РИМ” он в этом случае зашифровал бы в буквосочетание “ФМР”.

Итак, смещение K=3 или K=4 можно рассматривать как ключ шифра.

В таблице 2.6 показаны подстановки, соответствующие шифру Цезаря для латинского алфавита. Английская фраза (открытый текст) meet me after the toga party после шифрования примет следующий вид (шифрованный текст): PHHW PH DIWHU WKH WRJD SDUMB.

Послание Цезаря «VENI VIDI VICI» в переводе на русский язык означающее «Пришел. Увидел. Победил», направленное его другу Аминтию после победы над понтийским царем Фернаком, сыном Митридата, выглядело бы в зашифрованном виде так: YHQL YLGL YLFL.

 

Таблица 2.6

 

Подстановки по шифру Цезаря для латинского алфавита

 

A—> D	J—> M	S—> V
В —> Е	К —> N	Т —> W
С —> F	L—> O	U—> X
D —> G	M—> P	V—> Y
E —> H	N—> O	W—> Z
F —> I	O—> R	X —> А
G —> J	P—> S	Y—> B
H —> K	Q —> Т	Z—> C
I —> L	R—> U

 

Если каждой букве назначить числовой эквивалент (а = 1, b = 2 и т.д.), то алгоритм шифрования по Цезарю применительно к латинскому алфавиту можно выразить следующей формулой, которая показывает, каким образом каждая буква открытого текста p заменяется буквой шифрованного текста C:

С = Е(p) = (p + 3) mod(26).

Введем понятие обобщенного алгоритма (шифра) Цезаря, сдвиг K исходного алфавита в котором возможен на любую величину, но не больше, чем количество букв в применяемом алфавите минус 1. Для латинского алфавита обобщенный алгоритм Цезаря записывается формулой:

 

С = Е(р) = (р + K) mod(26),

 

где K принимает значения в диапазоне от 1 до 25. Алгоритм расшифровывания также прост:

p = D(С) = (С – K)mod(26)

Достоинством системы шифрования Цезаря является простота шифрования и расшифровывания. К недостаткам системы Цезаря следует отнести:

—   подстановки, выполняемые в соответствии с системой Цезаря, не маскируют частот появления различных букв исходного открытого текста;

— сохраняется алфавитный порядок в последовательности заменяющих букв; при изменении значения К изменяются только начальные позиции такой последовательности;

— число возможных ключей К мало;

— шифр Цезаря легко вскрывается на основе анализа частот появления букв в шифротексте и даже на основе простого перебора вариантов.

Две практические задачи криптоанализа: доказательство слабой криптографической стойкости алгоритма Цезаря и шифров моноалфавитной подстановки.

Если известно, что определенный текст был шифрован с помощью шифра Цезаря, то с помощью простого перебора всех вариантов раскрыть шифр очень просто – для этого достаточно проверить 25 возможных вариантов ключей. На рис. 2.19 показаны результаты применения этой стратегии к указанному выше первому сообщению. В данном случае открытый текст распознается в третьей строке.

Применение метода последовательного перебора всех возможных вариантов оправдано следующими тремя важными характеристиками данного шифра.

1. Известны алгоритмы шифрования и дешифрования.

2. Необходимо перебрать всего 25 вариантов.

3. Язык открытого текста известен и легко узнаваем.

В большинстве случаев, когда речь идет о защите сетей, можно предполагать, что алгоритм известен. Единственное, что делает криптоанализ на основе метода последовательного перебора практически бесполезным – это применение алгоритма, для которого требуется перебрать слишком много ключей. Например, алгоритм DES, использующий 56-битовые ключи, требует при последовательном переборе рассмотреть пространство из 2⁵⁶, или более чем 7х10¹⁶ ключей.

Третья характеристика также важна. Если язык, на котором написан открытый текст, неизвестен, то расшифровыванный текст можно не распознать. Более того, исходный текст может состоять из сокращений или быть каким-либо образом сжат – это также затрудняет распознавание.

Рассмотрим теперь более простую возможность повысить криптостойкость шифров моноалфавитной подстановки. Если в латинском алфавите шифротекста допустить использование любой из перестановок 26 символов алфавита, то мы получим 26!, или более чем 4х10²⁶ возможных ключей (ключ в данном случае – применяемый для записи шифротекста алфавит, полученный на основе перестановок символов обычного алфавита, а данный подход можно охарактеризовать как наивысший уровень развития идеи «шифра Цезаря»). Это на 10 порядков больше, чем размер пространства ключей DES, и это кажется достаточным для того, чтобы сделать невозможным успешное применение криптоанализа на основе метода последовательного перебора.

 

Рис. 2.19. Криптоанализ шифра Цезаря методом перебора всех вариантов ключей

Однако для криптоаналитика существует и другая линия атаки. Если криптоаналитик имеет представление о природе открытого текста (например, о том, что это несжатый текст на английском языке), можно использовать известную информацию о характерных признаках, присущих текстам на соответствующем языке. Чтобы показать, как этот подход применяется на практике, рассмотрим небольшой пример. Допустим, нам требуется расшифровать следующий шифрованный текст:

UZQSOVUOHXMOPVGPOZPEVSGZWSZOPFPESXUDBMETSXAIZ

VUEPHZHMDZSHZOWSFPAPPDTSVPQUZWYMXUZUHSX

EPYEPOPDZSZUFPOMBZWPFUPZHMDJUDTMOHMQ

На первом этапе можно определить относительную частоту появления в тексте различных букв и сравнить их со среднестатистическими данными для букв английского языка (рис. 2.20).

Рис. 2.20. Относительная частота появления букв в английском тексте

Если сообщение достаточно длинное, этой методики уже может быть достаточно для распознавания текста, но в нашем случае, когда сообщение небольшое, точного соответствия ожидать не приходится. В нашем случае относительная частота вхождения букв в шифрованном тексте (в процентах) оказывается следующей:

 

Сравнивая эти результаты с данными, показанными на рис. 2.20, можно заключить, что, скорее всего, буквы Р и Z шифрованного текста являются эквивалентами букв е и t открытого текста, хотя трудно сказать, какой именно букве – Р или Z – соответствует е, а какой – t. Буквы S, U, О, М и Н, обладающие относительно высокой частотой появления в тексте, скорее всего, соответствуют буквам из множества {г, n, i, о, а, s}. Буквы с низкой частотой появления (а именно А, В, G, Y, I, J), по-видимому, соответствуют буквам множества {w, v, b, k, x, q, j, z}.

Дальше можно пойти несколькими путями. Можно, например, принять какие-то предположения о соответствиях и на их основе попытаться восстановить открытый текст, чтобы увидеть, выглядит ли такой текст похожим на что-либо осмысленное. Более систематизированный подход заключается в продолжении поиска в тексте новых характерных закономерностей. Например, может быть известно, что в рассматриваемом тексте обязательно должны присутствовать некоторые слова. Или же можно искать повторяющиеся последовательности букв шифрованного текста и пытаться определить их эквиваленты в открытом тексте.

Один из очень эффективных методов заключается в подсчете частоты использования комбинаций, состоящих из двух букв. Такие комбинации называют биграммами. Для значений относительной частоты появления в тексте биграмм тоже можно построить гистограмму, подобную показанной на рис. 2.20. Известно, что в английском языке самой распространенной является биграмма th. В нашем шифрованном тексте чаще всего (три раза) встречается комбинация ZW. Поэтому можно предположить, что Z соответствует t а W – h. Тогда из ранее сформулированной гипотезы вытекает, что Р соответствует е. Заметим, что в шифрованном тексте буквосочетание ZWP имеется, и теперь мы можем представить его как the. В английском языке the является самой распространенной триграммой (т.е. комбинацией из трех букв), поэтому можно надеяться, что мы движемся в правильном направлении.

Теперь обратите внимание на комбинацию ZWSZ в первой строке. Конечно, мы не можем сказать с полной уверенностью, что эти буквы принадлежат одному и тому же слову, но, если предположить, что это так, они соответствуют слову thSt. Отсюда заключаем, что букве S соответствует а.

Теперь мы имеем следующий результат:

Выяснив значение всего лишь четырех букв, мы расшифровали уже значительную часть сообщения. Продолжая анализ частоты появления букв, а также применяя метод проб и ошибок, остается проделать совсем немного работы, чтобы получить окончательный ответ. Расшифровыванный исходный текст (с добавленными в него пробелами) имеет следующий вид:

it was disclosed yesterday that several informal but direct contacts have been made with political representatives of the viet cong in Moscow /вчера стало известно, что в Москве состоялся ряд неофициальных, но прямых контактов с политическими представителями вьетконга/