Согласно первому началу термодинамики при обратимых процессах энергообмена между системой и окружающей средой количество теплоты 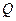 , полученное системой, расходуется на изменение внутренней энергии
, полученное системой, расходуется на изменение внутренней энергии 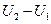 системы и совершение макроскопической работы
системы и совершение макроскопической работы 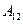 :
:
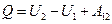 .
.
Здесь макроскопическая работа определяется формулой
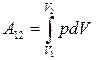 ,
,
где p – давление, V – объем, индексы 1 и 2 обозначают соответственно начальное и конечное равновесное состояние системы.
Внутренняя энергия идеального одноатомного газа зависит только от температуры T газа и описывается выражением
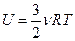 ,
,
где 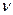 - число молей газа,
- число молей газа, 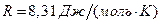 - универсальная газовая постоянная.
- универсальная газовая постоянная.
Уравнение состояние идеального газа (уравнение Клапейрона - Менделеева) имеет вид:
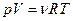 ,
,
где  , m – масса газа,
, m – масса газа, 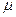 - молярная масса газа.
- молярная масса газа.
Задача №10
Определить изменение внутренней энергии 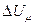 одного моля идеального одноатомного газа при изобарном изменении его объема от
одного моля идеального одноатомного газа при изобарном изменении его объема от 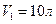 (
(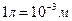 ) до
) до 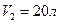 , если давление газа
, если давление газа 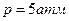 (
(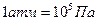 ).
).
Решение
Задача решается на основе формулы для внутренней энергии 1 моля идеального одноатомного газа
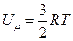 (4.10.1)
(4.10.1)
с использованием уравнения Клапейрона – Менделеева при 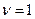
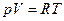 . (4.10.2)
. (4.10.2)
Согласно (1.1) изменение внутренней энергии
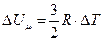 (4.10.3)
(4.10.3)
обусловлено изменением температуры 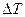 газа. Из уравнения (1.2) следует, что при постоянном давлении
газа. Из уравнения (1.2) следует, что при постоянном давлении
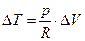 , (4.10.4)
, (4.10.4)
где 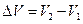 .
.
Подставляя (1.4) в (1.3), получим
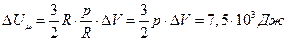 . (4.10.5)
. (4.10.5)
В процессе изобарного расширения газ совершил работу
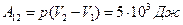
и получил извне количество теплоты
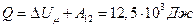 .
.
Ответ: 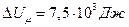 .
.
Конструкция любой тепловой машины содержит нагреватель, рабочее тело и холодильник. За один цикл рабочее тело получает от нагревателя количество теплоты 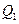 , которое частично расходуется на совершение макроскопической работы
, которое частично расходуется на совершение макроскопической работы 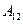 , а оставшееся количество теплоты
, а оставшееся количество теплоты 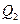 отдается холодильнику. В соответствии с первым началом термодинамики
отдается холодильнику. В соответствии с первым началом термодинамики
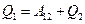 .
.
Затем цикл повторяется. Цикл Карно состоит из двух изотерм и двух адиабат, изображенных на диаграмме pV.
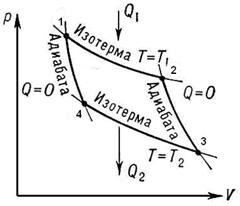
Здесь 1 – начальное равновесное состояние рабочего тела. Участок 12 – изотермическое расширение рабочего тела при температуре нагревателя 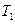 , где рабочее тело получает от нагревателя количество теплоты
, где рабочее тело получает от нагревателя количество теплоты 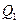 . Участок 23– адиабатное расширение рабочего тела. Участок 34-изотермическое сжатие рабочего тела при температуре холодильника
. Участок 23– адиабатное расширение рабочего тела. Участок 34-изотермическое сжатие рабочего тела при температуре холодильника 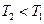 , где рабочее тело отдает холодильнику количество теплоты
, где рабочее тело отдает холодильнику количество теплоты 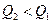 . Участок 41 – адиабатное сжатие рабочего тела и переход его в начальное состояние 1. Все процессы происходят обратимым образом и рабочее тело в любой точке цикла находится в равновесном состоянии. В этом случае выполняется равенство Клаузиуса
. Участок 41 – адиабатное сжатие рабочего тела и переход его в начальное состояние 1. Все процессы происходят обратимым образом и рабочее тело в любой точке цикла находится в равновесном состоянии. В этом случае выполняется равенство Клаузиуса
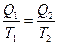 ,
,
а коэффициент полезного действия идеальной тепловой машины описывается формулами
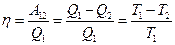
(определение к.п.д. с использованием первого начала термодинамики и равенства Клаузиуса для идеальной тепловой машины, работающей по циклу Карно).
Задача№11
Идеальная тепловая машина, работающая по циклу Карно, получает теплоту от нагревателя с температурой 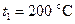 и отдает теплоту холодильнику с температурой
и отдает теплоту холодильнику с температурой 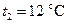 , совершая за один цикл работу
, совершая за один цикл работу 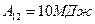 . Определить количество теплоты
. Определить количество теплоты 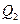 , отдаваемое холодильнику за один цикл.
, отдаваемое холодильнику за один цикл.
Решение
Задача решается с помощью формулы, которая выражает закон сохранения энергии для идеальной тепловой машины, работающей по циклу Карно,
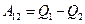 (4.11.1)
(4.11.1)
и равенства Клаузиуса для обратимых процессов
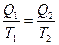 , (4.11.2)
, (4.11.2)
где 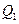 и
и 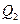 - количество теплоты, полученное от нагревателя с температурой
- количество теплоты, полученное от нагревателя с температурой 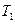 , и отданное холодильнику с температурой
, и отданное холодильнику с температурой 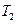 , соответственно.
, соответственно.
Исключая из системы уравнений (3.1) и (3.2) 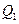 , получим
, получим
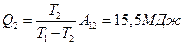 , (4.11.3)
, (4.11.3)
где 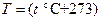 К.
К.
Ответ: 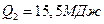 .
.
 2020-09-24
2020-09-24 104
104








