А.А. Колоколов
«Механика и молекулярная физика»
Методические указания к решению задач
для студентов I-го курса дневного отделения
Москва
2014
УДК
Колоколов А.А.
А.А.Колоколов. – М.: ГОУ ВПО МГТУ «СТАНКИН», 2014. – __с.
Методические указания предназначены для студентов первого курса…
УДК
© Колоколов А.А.
© ГОУ ВПО МГТУ «Станкин», 2014
Динамика материальной точки
В классической нерелятивистской механике, где скорость движения тел считается много меньше скорости света в вакууме 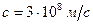 , основным законом динамики является II-ой закон Ньютона. Согласно этому закону в инерциальной системе отсчета первая производная импульса
, основным законом динамики является II-ой закон Ньютона. Согласно этому закону в инерциальной системе отсчета первая производная импульса 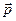 тела по времени
тела по времени 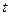 равна полной силе
равна полной силе  , действующей на это тело,
, действующей на это тело,
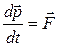 . .
| (1.0.1) |
Здесь  , m – инертная масса тела,
, m – инертная масса тела, 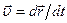 - мгновенная скорость тела,
- мгновенная скорость тела, 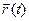 - радиус-вектор тела, определяющий его положение в выбранной инерциальной системе отсчета.
- радиус-вектор тела, определяющий его положение в выбранной инерциальной системе отсчета.
При определении мгновенной скорости тело рассматривается как материальная точка, т.е. линейные размеры тела считаются малыми по сравнению с характерными расстояниями решаемой задачи и не учитывается вращательное движение тела.
Если масса тела m при движении сохраняется постоянной, уравнение (1.0.1) упрощается и принимает вид
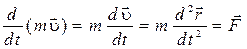 , ,
| (1.0.2) |
где 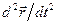 - мгновенное ускорение тела. Это обыкновенное дифференциальное уравнение второго порядка по времени. Для однозначного определения решения уравнения (1.0.2), т.е. нахождения функции
- мгновенное ускорение тела. Это обыкновенное дифференциальное уравнение второго порядка по времени. Для однозначного определения решения уравнения (1.0.2), т.е. нахождения функции 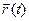 , необходимо в некоторый момент времени
, необходимо в некоторый момент времени 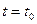 задать два начальных условия:
задать два начальных условия:
 , , 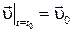 . .
| (1.0.3) |
В этом случае при заданной силе  все последующие состояния тела
все последующие состояния тела 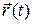 ,
, 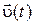 для
для 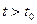 находятся однозначно.
находятся однозначно.
Определение движения тела по заданным начальным условиям и известной силе называется прямой задачей динамики. В обратной задаче требуется найти силу, которая обеспечивает необходимые характеристики движения тела (это задача управления движением тела).
Задача № 1
Два тела с массами m 1 и m 2 связаны между собой нерастяжимой и невесомой (m =0) нитью, перекинутой через невесомый блок (рис.1.1). Коэффициент трения скольжения между телом 1 и горизонтальной поверхностью μ=0,2. Ускорение свободного падения g =9,8м/с2. Блок считается невесомым. Трением в блоке можно пренебречь. Определить ускорения тел a 1 и a 2, если в начальный момент времени t =0 они были неподвижны. Рассмотреть два случая: 1) m 1=10кг, m 2=5кг; 2) m 1=10кг, m 2=1кг.
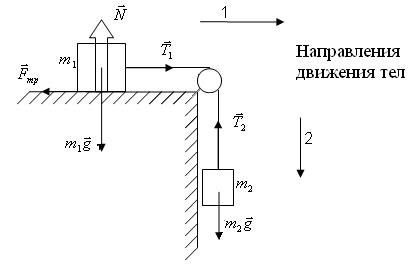
Рис.1.1
Решение
Это прямая задача динамики, где по заданным действующим силам необходимо рассчитать движение тел в системе с кинематическими связями. Решение задачи выполняется с помощью следующего алгоритма.
1. Укажем все силы, которые согласно условиям задачи действуют на тела системы с отличной от нуля массой (движение невесомых тел определяется связями): силы тяжести 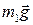 и
и 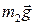 , силы натяжения
, силы натяжения 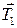 и
и 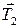 , сила реакции опоры
, сила реакции опоры 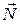 , сила трения
, сила трения 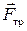 .
.
2. Согласно II-ому закону Ньютона запишем в векторной форме уравнения движения тел 1 и 2:
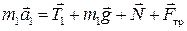 , ,
| (1.1.1) |
 . .
| (1.1.2) |
3. Поскольку тела движутся вдоль прямых, то удобно перейти от векторных уравнений к одномерным скалярным уравнениям, используя проекции уравнений (1.1.1)-(1.1.2) на направления соответствующих движений:
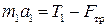 , ,
| (1.1.3) |
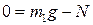 , ,
| (1.1.4) |
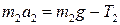 . .
| (1.1.5) |
В полученные 3 уравнения входят 6 неизвестных величин: a 1, a 2, T 1, T 2, N и F тр. Для однозначного нахождения всех 6 неизвестных систему уравнений (1.1.3)-(1.1.5) необходимо дополнить еще тремя независимыми уравнениями.
4. Для получения дополнительных уравнений воспользуемся условиями задачи и законами физики.
Поскольку нить нерастяжима, то величины ускорений должны быть одинаковыми:
 . .
| (1.1.6) |
Нить и блок считаются невесомыми, трение в блоке не учитывается, поэтому величины сил натяжения равны друг другу во всех точках нити:
| T 1= T 2= T. | (1.1.7) |
Сила трения имеет различную физическую природу и величину в зависимости от того, движется тело 1 относительно поверхности или нет:

| (1.1.8) |
Здесь F тр.п. – сила трения покоя и F тр.ск. – сила трения скольжения.
В зависимости от условий задачи возможны два решения.
I. Допустим, что действующие силы обеспечивают движение тел и
| F тр= F тр.ск.=μ N. | (1.1.9) |
В этом случае полная система уравнений принимает вид:
 , ,
| (1.1.10) |
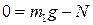 , ,
| (1.1.11) |
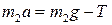 . .
| (1.1.12) |
Решая эту систему равнений, получим:
 , ,
| (1.1.13) |
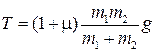 , ,
| (1.1.14) |
| N = m 1 g. | (1.1.15) |
Данное решение справедливо, если a >0 или m 2>μ m 1.
Физический смысл последнего условия заключается в том, что сила тяжести m 2 g, действующая на тело 2, должна превышать максимальное значение силы трения покоя 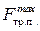 = F тр.ск.=μ N =μ m 1 g, действующей на тело 2 и препятствующей движению.
= F тр.ск.=μ N =μ m 1 g, действующей на тело 2 и препятствующей движению.
II. Если m 2<μ m 1, тела остаются в состоянии покоя и
| F тр= F тр.п.. | (1.1.16) |
Соответствующая полная система уравнений принимает вид (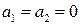 ):
):
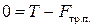 , ,
| (1.1.17) |
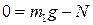 , ,
| (1.1.18) |
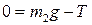 . .
| (1.1.19) |
Решение этой системы дает:
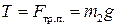 , ,
| (1.1.20) |
 . .
|
Для m 1=10кг, m 2=5кг и μ=0,2 справедливо условие m 2>μ m 1, поэтому тела движутся с ускорением
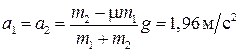 . .
| (1.1.21) |
При m 1=10кг, m 2=1кг и μ=0,2 выполняется условие m 2<μ m 1, сила трения покоя F тр.п.= m 2 g и тела остаются в состоянии покоя, когда
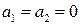 . .
| (1.1.21) |
Ответ: 1)  ; 2)
; 2) 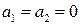 .
.
Задача №2
На краю горизонтального диска радиусом R =0,1м неподвижно лежит маленькая шайба (рис.2.1). В момент времени t =0 диск начинает вращаться вокруг вертикальной оси, проходящей через его центр, с угловым ускорением ε=1рад/с2. Через какое время t 1 шайба соскользнет с диска, если коэффициент скольжения между шайбой и поверхностью диска μ=0,2?
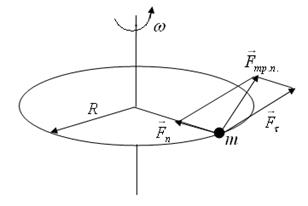
Рис.2.1
Угловая скорость ω и угловое ускорение ε определяются следующим образом
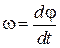 , , 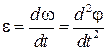
| (1.2.1) |
где φ - угол поворота диска вокруг вертикальной оси.
Шайба совершает ускоренное движение по окружности, где её ускорение 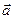 удобно представить в виде векторной суммы.
удобно представить в виде векторной суммы.
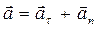 . .
| (1.2.2) |
Здесь 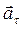 – тангенциальное ускорение, направленное по касательной к окружности
– тангенциальное ускорение, направленное по касательной к окружности
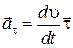 . .
| (1.2.3) |
где 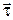 - единичный вектор касательной к окружности, направленный по вектору линейной скорости
- единичный вектор касательной к окружности, направленный по вектору линейной скорости  . Это ускорение определяет скорость изменения величины линейной скорости
. Это ускорение определяет скорость изменения величины линейной скорости 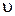 . Ускорение
. Ускорение 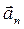 – нормальное ускорение, перпендикулярное к касательной окружности в точке нахождения шайбы и направленное к центру окружности
– нормальное ускорение, перпендикулярное к касательной окружности в точке нахождения шайбы и направленное к центру окружности
 . .
| (1.2.4) |
Единичный вектор нормали 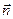 перпендикулярен к вектору
перпендикулярен к вектору 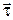 и направлен к центру окружности. Нормальное ускорение определяет скорость изменения направления вектора
и направлен к центру окружности. Нормальное ускорение определяет скорость изменения направления вектора  .
.
Решение
Это пример обратной задачи динамики, где по заданному ускорению тела требуется найти необходимую силу.
1. Определим все силы, которые действуют на шайбу согласно условиям задачи: сила тяжести 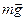 , сила реакции опоры
, сила реакции опоры 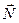 и сила трения покоя
и сила трения покоя 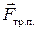 (шайба считается неподвижной относительно поверхности диска).
(шайба считается неподвижной относительно поверхности диска).
2. Запишем в векторной форме уравнение движения шайбы в лабораторной системе отсчета:
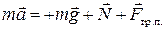 . .
| (1.2.5) |
Поскольку ускорение шайбы в вертикальном направлении равно нулю, то
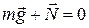
| (1.2.6) |
и уравнение (1.2.5) упрощается:
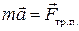
| (1.2.7) |
Используя разложение полного ускорения шайбы на тангенциальное 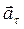 и нормальное
и нормальное 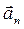 ускорения, запишем уравнение (1.2.7) в виде:
ускорения, запишем уравнение (1.2.7) в виде:
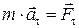 , , 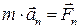
| (1.2.8) |
где 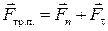 .
.
3. Перейдем от векторной формы записи уравнения (1.2.8) к скалярной, используя проекции на направления ускорений 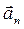 и
и 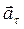 ,
,
 , , 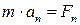
| (1.2.9) |
4. Определим зависимость величины полного ускорения шайбы
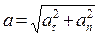
| (1.2.10) |
от времени. Согласно определению
 . .
| (1.2.11) |
Здесь использована известная формула для линейной скорости материальной точки, движущейся по окружности, 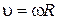 .
.
Нормальное ускорение определяется выражением
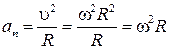 , ,
| (1.2.12) |
в которое входит неизвестная угловая скорость ω(t). Для нахождения ω(t) используем определение углового ускорения
 . .
| (1.2.13) |
Разделим в этом дифференциальном уравнении относительно угловой скорости переменные ω и 

| (1.2.14) |
и проинтегрируем левую часть по времени от t =0 до текущего момента времени t, а правую часть по угловой скорости от начального значения 0 до текущего значения ω(t)
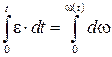 . .
| (1.2.15) |
Выполняя интегрирование
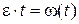
| (1.2.16) |
и подставляя (1.2.16) в (1.2.10), найдем, что
 . .
| (1.2.17) |
Из (1.2.10), (1.2.11) и (1.2.17) следует, что величина полного ускорения
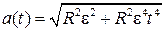
| (1.2.18) |
монотонно растет со временем.
5. В соответствии с ростом величины ускорения должна расти сила трения покоя, обеспечивающая это ускорение,
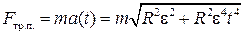 . .
| (1.2.19) |
Однако величина силы трения покоя ограничена сверху величиной силы трения скольжения F тр.ск.=μ N =μ mg:
| F тр.п.≤ μ mg, | (1.2.20) |
поэтому условие движения шайбы вместе с диском принимает вид
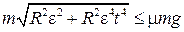 . .
| (1.2.21) |
Отсюда находим, что в момент времени t 1, когда
 , ,
| (1.2.22) |
шайба слетит с диска. Таким образом,
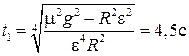 . .
| (1.2.23) |
Отметим, что при μ g < R ε шайба слетит с диска сразу после начала вращения.
Ответ: t 1=4,5с.
Задача №3
Автомобиль массой m =2000кг движется прямолинейно со скоростью υ0=72км/ч. В момент времени t =0 на него начинает действовать тормозящая сила, линейно растущая со временем согласно формуле  , где
, где 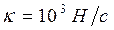 . Определите время t 1, необходимое для полной остановки автомобиля, и соответствующий тормозной путь S 1.
. Определите время t 1, необходимое для полной остановки автомобиля, и соответствующий тормозной путь S 1.
Решение
Это прямая задача механики, где по заданной силе необходимо определить движение тела.
1. При t >0 на автомобиль действует единственная горизонтальная сила 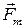 , направленная против вектора скорости автомобиля. Векторное уравнение движения автомобиля в горизонтальной плоскости запишется следующим образом:
, направленная против вектора скорости автомобиля. Векторное уравнение движения автомобиля в горизонтальной плоскости запишется следующим образом:
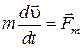 . .
| (1.3.1) |
2. Перейдем к скалярной форме записи с помощью проекции уравнения (1.3.1) на направление вектора скорости 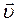 :
:
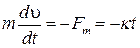 . .
| (1.3.2) |
Это обыкновенное дифференциальное уравнение первого порядка по времени относительно неизвестной функции υ.
3. Дифференциальное уравнение (1.3.2) решается методом разделения переменных υ и t:
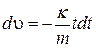 . .
| (1.3.3) |
Проинтегрируем левую часть по скорости от её начального значения υ0 до текущей величины υ(t), а правую часть по времени от начального момента t =0 до текущего момента времени t
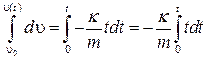 . .
| (1.3.4) |
Выполняя интегрирование, получим
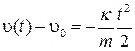
| (1.3.5) |
или
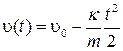 . .
| (1.3.6) |
4. В момент остановки автомобиля t = t 1
 , ,
| (1.3.7) |
поэтому из (1.3.6) находим, что
 . .
| (1.3.8) |
5. Тормозной путь S 1 находится с помощью определения величины скорости для прямолинейного движения:
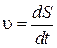 , ,
| (1.3.9) |
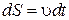 , ,
| (1.3.10) |

| |

| (1.3.11) |
Ответ: t 1=8,94с; S 1=119м.
2. Гармонические колебания. Кинематика гармонических колебаний. Свободные незатухающие колебания
Рассмотрим одномерное движение частицы массой m вдоль оси х под действием консервативной силы:
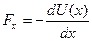 , ,
| (2.0.1) |
где U (x) – потенциальная энергия частицы.
Согласно II-ому закону Ньютона уравнение движения частицы имеет вид:
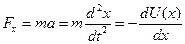 . .
| (2.0.2) |
Нас интересуют возможные положения равновесия частицы, где скорость, ускорение и действующая на частицу сила равны нулю:

| (2.0.3) |
Согласно (2.0.2) в положении равновесия производная потенциальной энергии по координате обращается в ноль,
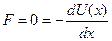 , ,
| (3.0.4) |
поэтому потенциальная энергия  в этих точках имеет экстремум и принимает либо максимальное, либо минимальное значение (точки перегиба здесь не рассматривается). Максимум потенциальной энергии соответствует неустойчивому положению равновесия, поскольку при сколь угодно малом отклонении частицы от данного положения равновесия частица под действием силы
в этих точках имеет экстремум и принимает либо максимальное, либо минимальное значение (точки перегиба здесь не рассматривается). Максимум потенциальной энергии соответствует неустойчивому положению равновесия, поскольку при сколь угодно малом отклонении частицы от данного положения равновесия частица под действием силы  будет удаляться от исходного положения. В точке минимума потенциальной энергии имеет место устойчивое положение равновесия. В этом случае частица, выведенная из положения равновесия внешним воздействием, стремится вернуться в исходное положение под действием возвращающей силы. При любом смещении частицы из положения устойчивого равновесия возвращающая сила всегда направлена к точке равновесия.
будет удаляться от исходного положения. В точке минимума потенциальной энергии имеет место устойчивое положение равновесия. В этом случае частица, выведенная из положения равновесия внешним воздействием, стремится вернуться в исходное положение под действием возвращающей силы. При любом смещении частицы из положения устойчивого равновесия возвращающая сила всегда направлена к точке равновесия.
Наше рассмотрение ограничено важным частным случаем движения частицы в малой окрестности устойчивого положения равновесия в точке х =0, когда потенциальная энергия описывается формулой:
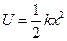 . .
| (2.0.6) |
Здесь k >0 – постоянная величина.
Для этого случая уравнение движения частицы записывается следующим образом:
 , ,
| (2.0.7) |
или
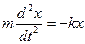 . .
| (2.0.8) |
Перенесем член - kx в левую часть равенства с изменением знака и получим следующее уравнение:
 . .
| (2.0.9) |
Разделим левую и правую части полученного уравнения на массу m
 , ,
| (2.0.10) |
и введем обозначение 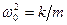 . В результате приходим к дифференциальному уравнению вида
. В результате приходим к дифференциальному уравнению вида
 . .
| (2.0.11) |
Данное обыкновенное дифференциальное уравнение второго порядка по времени описывает механическую систему, которая называется гармоническим осциллятором. Примером гармонического осциллятора может служить шарик, подвешенный на вертикальной пружине.
Общее решение полученного дифференциального уравнения может быть записано в виде:
 , ,
| (2.0.12) |
где 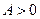 – амплитуда гармонических колебаний,
– амплитуда гармонических колебаний, 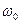 – круговая, или циклическая частота колебаний, связанная с частотой колебаний
– круговая, или циклическая частота колебаний, связанная с частотой колебаний  . Аргумент косинуса называется фазой колебаний, а постоянная
. Аргумент косинуса называется фазой колебаний, а постоянная 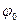 - начальной фазой. При подстановке функции (2.0.12) в дифференциальное уравнение (2.0.11) это уравнение превращается в числовое тождество
- начальной фазой. При подстановке функции (2.0.12) в дифференциальное уравнение (2.0.11) это уравнение превращается в числовое тождество  для всех моментов времени.
для всех моментов времени.
Неизвестные величины А и 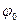 находятся с помощью двух начальных условий, определяющих начальное состояние частицы и обычно задаваемых для момента времени t =0,
находятся с помощью двух начальных условий, определяющих начальное состояние частицы и обычно задаваемых для момента времени t =0,
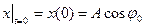 , , 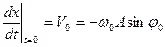 . .
| (2.0.13) |
Из начальных условий (3.0.13) следует, что
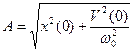 , , 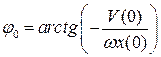 . .
| (2.0.14) |
Число начальных условий должно равняться числу неизвестных постоянных в общем решении обыкновенного дифференциального уравнения. В свою очередь число произвольных постоянных в общем решении обыкновенного дифференциального уравнения равно порядку этого уравнения, который определяется высшей производной искомой функции по времени.
Приведённое выше решение уравнения гармонического осциллятора описывает свободные незатухающие колебания. Смещение x, скорость V и ускорение a данных колебаний определяются формулами:
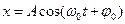 , ,
| (2.0.15) |
 , ,
| (2.0.16) |
 . .
| (2.0.17) |
В случае свободных незатухающих гармонических колебаний полная механическая энергия осциллятора Е сохраняется постоянной. Она равна сумме его кинетической
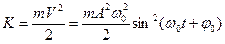
| (2.0.18) |
и потенциальной
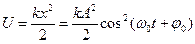
| (2.0.19) |
энергий. С учетом (2.0.12) выражение для полной энергии принимает вид:
 . .
| (2.0.20) |
Здесь использовано соотношение  .
.
Задача №4
Найти результирующее движение  в случае двух гармонических колебаний одинаковой частоты, происходящий вдоль оси х с амплитудами А и В.
в случае двух гармонических колебаний одинаковой частоты, происходящий вдоль оси х с амплитудами А и В.
Решение
1. Задача решается методом векторных диаграмм. Будем рассматривать смещение x как проекцию на ось x вектора постоянной длины A, который вращается с постоянной угловой скоростью ω в плоскости X0Y вокруг точки x=y= 0
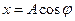 , ,
| (2.4.1) |
где  . Формула (2.4.1) описывает гармонические колебания вдоль оси x с циклической частотой
. Формула (2.4.1) описывает гармонические колебания вдоль оси x с циклической частотой 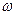 , амплитудой A и начальной фазой
, амплитудой A и начальной фазой  .
.
2. Если частица одновременно участвует в двух гармонических колебаниях вдоль оси x, то для начального момента времени t =0 из одной точки x=y=0 строятся два вектора, положение и длина которых определяются соответственно амплитудой и начальной фазой этих колебаний. Суммарное движение частицы описывается вектором, равным сумме этих двух векторов.
3. Найдем графически сумму двух гармонических колебаний
 . .
| (2.4.2) |
Из точки О, как показано на рис.4.1, построим два вектора, соответствующие гармоническим колебаниям в начальный момент времени t =0. Суммарный вектор  имеет длину
имеет длину
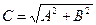
| (2.4.3) |
и начальную фазу
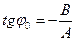 . .
| (2.4.4) |
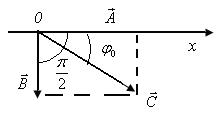
Рис.4.1
При t >0 все три вектора  ,
,  и
и  вращаются с одинаковой угловой скоростью ω, равной частоте гармонических колебаний. Проекция вектора
вращаются с одинаковой угловой скоростью ω, равной частоте гармонических колебаний. Проекция вектора  на ось х описывает результирующее движение частицы в виде
на ось х описывает результирующее движение частицы в виде
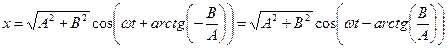 . .
| (2.4.5) |
Ответ:  .
.
Задача №5
Частица совершает гармонические колебания около положения равновесия х =0 с циклической частотой ω=4 рад/с так, что в начальный момент времени t =0 её координата x 0=0,25м, а скорость V 0=1м/с. Найдите смещение частицы x (t) как функцию времени t.
Решение
1. Общее выражение, описывающее гармонические незатухающие колебания, имеет вид:
 , ,
| (2.5.1) |
где А, ω и φ0 - постоянные величины. Согласно условиям задачи известны циклическая частота
| ω=4 рад/с | (2.5.2) |
и состояние частицы в момент времени t =0:
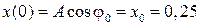 м , м ,
| (2.5.3) |
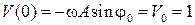 м/с2 . м/с2 .
| (2.5.4) |
2. Из (2.5.3) и (2.5.4) получаем, что амплитуда колебаний
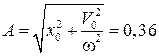 м м
| (2.5.5) |
и начальная фаза
 . .
| (2.5.6) |
3. C учётом (2.5.5) и (2.5.6) выражение (2.5.1) принимает вид
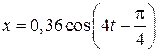 м, м,
| (2.5.7) |
где время t измеряется в секундах.
Ответ: 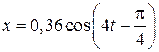 м, где время t измеряется в секундах.
м, где время t измеряется в секундах.
Задача №6
Рассмотреть движение тела массой m =1 кг в колебательных системах 1 и 2, показанных на рис.6.2. Коэффициенты жёсткости пружины 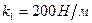 и
и 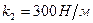 . Массами пружин и трением можно пренебречь. Определите периоды T 1 и T 2 гармонических колебаний тела в этих системах.
. Массами пружин и трением можно пренебречь. Определите периоды T 1 и T 2 гармонических колебаний тела в этих системах.
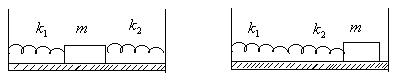
Система 1 Система 2
Рис.6.2
Решение
Для расчёта механической колебательной системы необходимо: 1) найти положение равновесия системы, 2) проанализировать его устойчивость, записав выражение для силы, возникающей при малом смещении тела из положения равновесия и 3) получить уравнение движения тела в малой окрестности устойчивого положения равновесия, записав его в стандартной форме уравнения движения гармонического осциллятора.
Определим все силы, действующие на тело согласно условиям задачи: сила тяжести 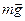 , сила реакции опоры
, сила реакции опоры 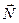 , силы упругости деформированных пружин
, силы упругости деформированных пружин 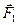 и
и 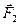 . В нашем случае достаточно рассмотреть только горизонтальное движение тела, поскольку вертикально направленные силы взаимно скомпенсированы.
. В нашем случае достаточно рассмотреть только горизонтальное движение тела, поскольку вертикально направленные силы взаимно скомпенсированы.
Очевидно, что в обеих системах имеются положения равновесия, причем будем считать, что для системы 1 в положении равновесия обе пружины не деформированы. Для каждой системы введём ось х, вдоль которой происходит движение тела, и направим её слева направо. При этом примем, что положение равновесия находится в точке х =0.
Система 1
1. Определим устойчивость положения равновесия. При смещении тела относительно равновесия пружины деформируется таким образом, что возникающие силы упругости обеих пружин направлены в одну сторону – к положению равновесия тела. Следовательно, формируется возвращающая сила и положение равновесия устойчивое.
2. Если смещение тела относительно положения равновесия х, полная сила упругости, действующая на тело,
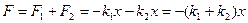 . .
| (2.6.1) |
Здесь учитывается то обстоятельство, что смещения тела и прикреплённых к нему концов пружины одинаковые.
3. Согласно II - ому закону Ньютона уравнение движения тела имеет вид:
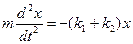
| (2.6.2) |
или
 , ,
| (2.6.3) |
где
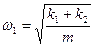
| (2.6.4) |
- циклическая частота и
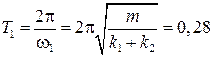 с с
| (2.6.5) |
- период гармонических колебаний тела в системе 1.
Система 2
1. Определим устойчивость положения равновесия. При смещении тела относительно положения равновесия пружины деформируются таким образом, что возникающие силы упругости обеих пружин направлены в одну сторону – к положению равновесия тела. Следовательно, формируется возвращающая сила и положение равновесия устойчивое.
2. Смещение х тела относительно положения равновесия равно сумме смещений правых концов обеих пружин
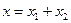 , ,
| (2.6.6) |
при этом на тело действует сила упругости только пружины 2
 . .
| (2.6.7) |
3. Согласно II – ому закону Ньютона уравнение движения тела запишется в виде
 . .
| (2.6.8) |
4. Поскольку пружины считаются невесомыми, то согласно III – ему закону Ньютона для сил упругости пружин выполняется равенство
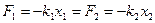
| (2.6.9) |
и
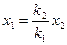 . .
| (2.6.10) |
Тогда из (2.6.6) и (2.6.10) следует, что
 . .
| (2.6.11) |
5. С учётом (2.6.11) уравнение движения тела (2.6.8) запишется следующим образом:
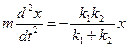
| (2.6.12) |
или
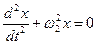 , ,
| (2.6.13) |
где

| (2.6.14) |
- циклическая частота и
 с с
| (2.6.15) |
- период гармонических колебаний тела в системе 2.
Согласно полученным результатам эквивалентная жёсткость k пружин в системе 1 определяется формулой
 , ,
|
а в системе 2 – формулой
 . .
|
Ответ:  с,
с, 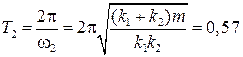 с.
с.
Динамика вращательного движения твердого тела. Закон сохранения момента импульса
Для описания вращения тела вокруг неподвижной оси используются следующие физические величины:
1. Момент инерции тела I относительно заданной оси, характеризующий инертность тела в отношении вращательного движения.
2. Момент импульса тела L=I w относительно заданной оси, являющийся количественной мерой вращательного движения тела, ω– угловая скорость вращения тела вокруг оси.
3. Момент силы М относительно заданной оси, который действует на тело и определяет скорость изменения во времени его момента импульса относительно оси вращения
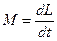 . .
| (3.0.1) |
Если при вращении момент инерции тела остается постоянным, то уравнение вращательного движения преобразуется к виду:
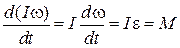 , ,
| (3.0.2) |
где 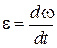 – угловое ускорение тела.
– угловое ускорение тела.
При описании вращательного движения твердого тела вокруг неподвижной точки используется момент импульса относительно точки, который определяется с помощью векторного произведения
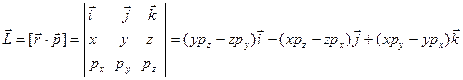 , ,
| (3.0.3) |
где  – радиус-вектор, проведенный из выбранной точки в ту точку, где находится начало вектора импульса
– радиус-вектор, проведенный из выбранной точки в ту точку, где находится начало вектора импульса 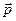 (в точку нахождения частицы).
(в точку нахождения частицы).
Аналогично можно определить вектор момента 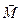 силы
силы  относительно заданной точки
относительно заданной точки
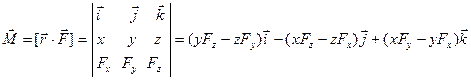 . .
| (3.0.4) |
Момент импульса  или силы
или силы  относительно точки О обозначается как
относительно точки О обозначается как  или
или  (рис. 3.01).
(рис. 3.01).

Рис. 3.01
Точка О – начало координат, 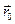 – радиус-вектор точки O ´, где находится начало вектора
– радиус-вектор точки O ´, где находится начало вектора 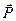 и точка приложения силы
и точка приложения силы  .
.
Рассмотрим проекцию вектора 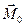 на ось z, проходящую через точку О. Из выражения (3.0.4) получим:
на ось z, проходящую через точку О. Из выражения (3.0.4) получим:
 . .
| (3.0.5) |
Величина Mz называется моментом силы  относительно заданной оси z. Важно отметить, что Mz не зависит от координаты z точки приложения силы и определяется только той компонентой силы, которая лежит в плоскости, перпендикулярной оси z. Эта компонента обозначается
относительно заданной оси z. Важно отметить, что Mz не зависит от координаты z точки приложения силы и определяется только той компонентой силы, которая лежит в плоскости, перпендикулярной оси z. Эта компонента обозначается  . Соответственно,
. Соответственно, 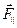 обозначает компоненту силы, параллельную оси z (рис. 3.02). Таким образом, полная сила
обозначает компоненту силы, параллельную оси z (рис. 3.02). Таким образом, полная сила
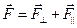 . .
| (3.0.6) |
Момент силы  относительно оси z можно записать следующим образом:
относительно оси z можно записать следующим образом:
 . .
| (3.0.7) |
Длина отрезка 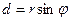 , перпендикулярного к его компоненте силы
, перпендикулярного к его компоненте силы  , называется плечом силы
, называется плечом силы 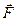 , j – угол между радиусом-вектором
, j – угол между радиусом-вектором 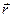 и компонентой силы
и компонентой силы  . Отрезки прямых d, r и
. Отрезки прямых d, r и 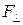 лежат в плоскости проходящей через точку O ´ приложении силы
лежат в плоскости проходящей через точку O ´ приложении силы  перпендикулярно оси z. Выбор знака в формуле (3.0.7) зависит от ориентации вектора
перпендикулярно оси z. Выбор знака в формуле (3.0.7) зависит от ориентации вектора  относительно оси z.
относительно оси z.

Рис. 3.02
Точка О – точка пересечения плоскости, проходящей через точку O ´ приложения силы 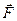 перпендикулярно оси z.
перпендикулярно оси z.
Для описания вращения твердого тела вокруг неподвижной оси используется уравнение моментов относительно этой оси
 , ,
| (3.0.8) |
где
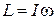
| (3.0.9) |
- момент импульса твердого тела относительно оси вращения, I – момент инерции твердого тела относительно этой оси, ω - угловая скорость вращения твердого тела и 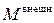 - момент всех внешних сил, действующих на тело, относительно рассматриваемой оси. Согласно третьему закону Ньютона, суммарный момент всех внутренних сил относительно произвольной оси всегда равен нулю.
- момент всех внешних сил, действующих на тело, относительно рассматриваемой оси. Согласно третьему закону Ньютона, суммарный момент всех внутренних сил относительно произвольной оси всегда равен нулю.
Если при вращении твердого тела его момент инерции сохраняется постоянным, уравнение моментов относительно неподвижной оси упрощается и принимает вид:
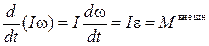 , ,
| (3.0.10) |
где

| (3.0.10) |
-угловое ускорение твердого тела и φ - угол поворота твердого тела вокруг оси вращения.
Из уравнения моментов относительно неподвижной оси следует, что момент импульса относительно этой оси сохраняется постоянным
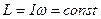 , ,
| (3.0.11) |
если полный момент всех внешних сил, действующих на твердое тело, относительно рассматриваемой оси равен нулю
| М внешн = 0. | (3.0.12) |
Кинетическая энергия K твердого тела, вращающегося вокруг неподвижной оси, описывается выражением
 . .
| (3.0.13) |
Изменение кинетической энергии K может быть обусловлено работой как внешних, так и внутренних сил, поэтому
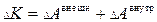 . .
| (3.0.14) |
При повороте абсолютно твердого тела на бесконечно малый угол Δφ работа внешних сил
| Δ А внешн = М внешнΔφ. | (3.0.15) |
Если полный момент внешних сил, действующих на тело равен нулю, то изменение кинетической энергии вращающегося тела возможно за счет работы внутренних сил, которая меняет момент инерции твердого тела
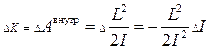 . .
| (3.0.16) |
Здесь L = const, поскольку М внешн= 0.
Задача №7
В устройстве, показанном на рис.7.1, определите ускорения тел с массами m 1 и m 2 (m 1 > m 2), связанных невесомой, нерастяжимой нитью, перекинутой через блок. Блок представляет собой однородный цилиндр с массой М и радиусом R. Нить по блоку не проскальзывает, трение в оси блока пренебрежимо мало. Ускорение свободного падения g.
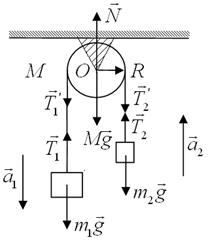
Рис.7.1
Решение
1. Определим все силы, действующие на тела системы с отличной от нуля массой: силы тяжести 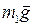 ,
, 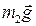 ,
, 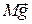 , силы натяжения нити
, силы натяжения нити 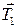 ,
, 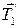 ,
,  ,
, 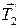 и сила реакции
и сила реакции  крепления блока.
крепления блока.
2. Запишем в векторной форме уравнения поступательного движения тел 1 и 2
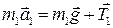 , ,
| (3.7.1) |
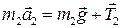 . .
| (3.7.2) |
Для блока поступательное движение отсутствует, поэтому
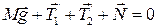 . .
| (3.7.3) |
Блок совершает вращательное движение вокруг своей оси симметрии, проходящей через центр масс блока перпендикулярно плоскости рисунка. Уравнение моментов относительно оси вращения блока имеет вид
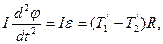
| (3.7.4) |
где момент инерции однородного блока относительно его оси симметрии

| (3.7.5) |
3. Перейдем от векторной формы записи уравнений (3.7.1) - (3.7.2) к скалярной, используя проекции этих уравнений на направления ускорений тел 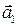 и
и 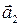
 , ,
| (3.7.6) |
 , ,
| (3.7.7) |
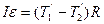 , ,
| (3.7.8) |
которая содержит 7 неизвестных величин:  .
.
4. Получим полную систему из 7 независимых уравнений, используя законы физики и условия задачи.
Благодаря нерастяжимости нити величины ускорений тел одинаковые:
 . .
| (3.7.9) |
Поскольку нить не проскальзывает по поверхности блока, то в каждой точке контакта линейные скорости элементов нити υ и поверхности блока ω R равны по величине
| υ=ω R . | (3.7.10) |
Отсюда получаем, что величины ускорения a тел и углового ускорения ε блока связаны соотношением
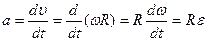 . .
| (3.7.11) |
Согласно условию задачи нить невесомая, поэтому сила натяжения одинаковая во всех точках нити слева от блока
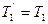 , ,
| (3.7.12) |
и во всех точках нити справа от блока
 . .
| (3.7.13) |
На основе уравнений (3.7.6) – (3.7.13) приходим к полной системе из 4 независимых уравнений для нахождения 4 неизвестных величин:
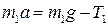 , ,
| (3.7.14) |
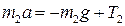 , ,
| (3.7.15) |
 , ,
| (3.7.16) |
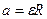 . .
| (3.7.17) |
5. Решая систему уравнений (3.7.14) – (3.7.17), находим величину ускорения тел
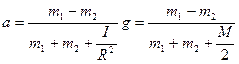 . .
| (3.7.18) |
Согласно полученному результату учет массы блока уменьшает ускорение тел.
Ответ: 
 .
.
Задача №8
Маховик в виде однородного диска с массой m= 10кг и радиусом R= 0,2м вращается вокруг своей оси симметрии с начальной угловой скоростью ω0=100рад/с. В момент времени t =0 к маховику начинают прижимать две тормозные колодки с силой F =50H каждая (рис.17.1). Коэффициент трения скольжения между маховиком и тормозными колодками μ=0,3. Определите изменение во времени угловой скорости ω(t) вращения маховика. Через какое время t 1 маховик остановиться?

Рис.8.1
Решение
Уравнение моментов относительно оси вращения маховика имеет вид
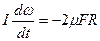 , ,
| (3.8.1) |
где μ F – сила трения скольжения между маховиком и тормозной колодкой и

| (3.8.2) |
-момент инерции маховика относительно его оси симметрии.
Разделим переменные ω и t в дифференциальном уравнении (3.8.1)
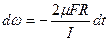
| (3.8.3) |
и проинтегрируем левую часть полученного равенства по ω от начальной угловой скорости ω о до текущей угловой скорости ω(t), а правую часть по t от начального момента времени t =0до текущего момента t

| (3.8.4) |
Выполняя интегрирование, получим зависимость угловой скорости маховика от времени
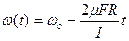 . .
| (3.8.5) |
Время t 1, через которое маховик остановится, находится с помощью уравнения
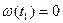 . .
| (3.8.6) |
Отсюда следует, что время остановки маховика
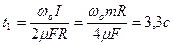 . .
| (3.8.7) |
Ответ: 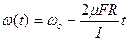 ,
, 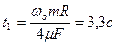 .
.
Задача №9
Однородный цилиндр массой с m и радиусом R скатывается без проскальзывания по наклонной плоскости с углом наклона α относительно горизонтали (рис.9.1). Ускорение свободного падения g. Определите ускорение  центра масс цилиндра. Как со временем изменяется скорость υ центра масс цилиндра, если его начальная скорость равнялась нулю?
центра масс цилиндра. Как со временем изменяется скорость υ центра масс цилиндра, если его начальная скорость равнялась нулю?
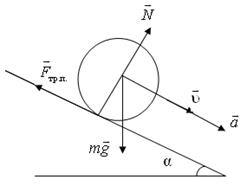
Рис.9.1
Решение
1.Определим все силы, которые действуют на цилиндр согласно условиям задачи: сила тяжести
 2020-09-24
2020-09-24 417
417







