2020-09-24
6396
Двух световых волн. Связь между разностью фаз
И оптической разностью хода двух интерферирующих волн.
Общая схема получения интерференционной картины.
Мы уже обсуждали, что реальные световые волны не являются строго монохроматическими в силу фундаментальных физических причин. Волны от двух независимых источников некогерентны и не могут дать интерференционной картины.
Когерентные световые волны можно получить, разделив (например, с помощью отражений или преломлений) волну, излучаемую одним источником, на две части.
Если заставить эти волны пройти разные оптические длины пути, а потом наложить друг на друга, будет наблюдаться интерференция.
Оптической длиной пути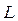 
называется произведение геометрической длины пути светового луча 
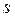на абсолютный показатель преломления 
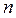среды, в которой этот путь пройден.
Пусть разделение на две когерентные волны происходит в точке О (рис. 6.1.2). До точки Р первая волна проходит в среде с показателем преломления n 1 геометрический путь s 1. Вторая волна проходит в среде с показателем преломления n 2геометрическийпуть s 2.
Если в точке О фаза колебания равна w t, то первая волна возбудит в точке Р колебания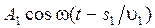 
. А вторая волна – колебание 
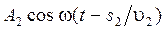. Здесь 
, 
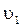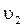– фазовые скорости волны в первой и во второй средах соответственно.
По определению абсолютного показателя преломления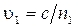 
, 
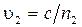. Разность фаз колебаний, возбуждаемых волнами в точке Р, будет равна:
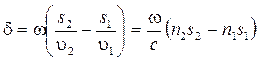. (6.1.5)
 |
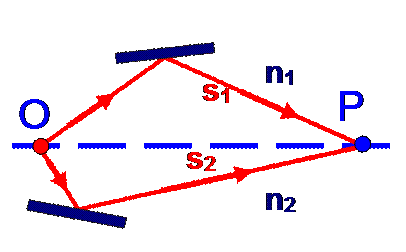| Рис. 6.1.2. Общая схема получения интерференционной картины |
Величина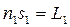 
представляет собой оптическую длину пути в среде споказателем преломления n 1. Величина 
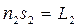– соответственно оптическая длина пути в среде с показателем преломления n 2.
Разность оптических длин путей называется оптической разностью хода волн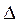 
:
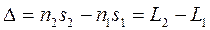. (6.1.6)
|
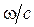как 
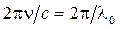(где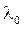 
- длина волны в вакууме), получим связь между разностью фаз δ и оптической разностью хода 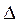двух интерферирующих волн: 
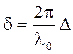. (6.1.7)
