2020-09-24
96
Тема 8
Отражение и преломление плоских волн.
При решении многих практически важных задач нельзя считать, что среда является однородной. На структуру поля и характер распространения волны существенно влияет граница раздела сред, обладающих разными свойствами. Попадая на поверхность раздела двух сред, электромагнитная волна может частично (или полностью) отразиться либо частично (либо полностью) пройти в другую среду. Кроме того, возможно и более сложное явление, называемое дифракцией волн.
Рассматриваем задачу такого типа: падение плоской электромагнитной волны на плоскую бесконечно протяженную границу раздела двух однородных изотропных сред. При анализе распространения плоской электромагнитной волны в неограниченной однородной среде использована прямоугольная система координат, одна из осей которой (ось 
) совпадала с направлением распространения волны.
Рассмотрим линейно поляризованную волну. Предположим, что волна распространяется в однородной изотропной среде вдоль оси 
, образующей с осями 
прямоугольной системы координат углы 
соответственно (рис.23). Поле однородной плоской волны в среде без потерь можно представить в виде
(1)
где 
- переменная, определяющая положение точки на оси 
.
Векторы 
и 
не зависят от координат и лежат в плоскостях, перпендикулярных оси , причем
(2)
где 
- координатный орт переменной 
. Поверхности равных фаз волны (1) образуют семейство плоскостей, перпендикулярных оси Z', и удовлетворяют уравнению 
, где 
- радиус-вектор, проведенный из начала координат до произвольной точки, лежащей на рассматриваемой ПРФ. Для перехода к координатам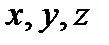 
нужно вычислить скалярное произведение вектора на вектор 
. Учитывая, что 
, запишем
(3)
Подставляя выражение (3) в (1), получаем
(4)
Если проводимость среды отлична от нуля, то в формуле (4) нужно параметр 
считать комплексной величиной, равной 
, векторы 
и 
- значениями комплексных амплитуд векторов 
в начале координат, a 
в соотношении (2) заменить на 
.
Прежде чем перейти к анализу волновых явлений на границе раздела двух сред, введем некоторые определения. Назовем плоскость, проходящую через нормаль к поверхности раздела двух сред параллельно направлению распространения волны, плоскостью падения. Вектор напряженности электрического поля плоской волны перпендикулярен направлению ее распространения, а по отношению к плоскости падения может быть ориентирован произвольно. Однако, не нарушая общности анализа, можно ограничиться рассмотрением двух ориентаций вектора 
, а именно:
вектор 
перпендикулярен плоскости падения (нормально поляризованная плоская волна);
вектор 
параллелен плоскости падения (параллельно поляризованная плоская волна).
Очевидно, что волну с любой другой ориентацией вектора 
, а также волны, имеющие круговую или эллиптическую поляризацию, можно представить в виде суперпозиции двух волн, одна из которых является нормально поляризованной, а вторая - параллельно поляризованной.
