2020-09-24
303
Тема: Определение максимума мощности в цепи постоянного тока с применением производной.
Цель работы: Корректировать знания, умения и навыки по теме: «Дифференциальное и интегральное исчисление».
Задание: Выполните задание по чертежу:
| 1. |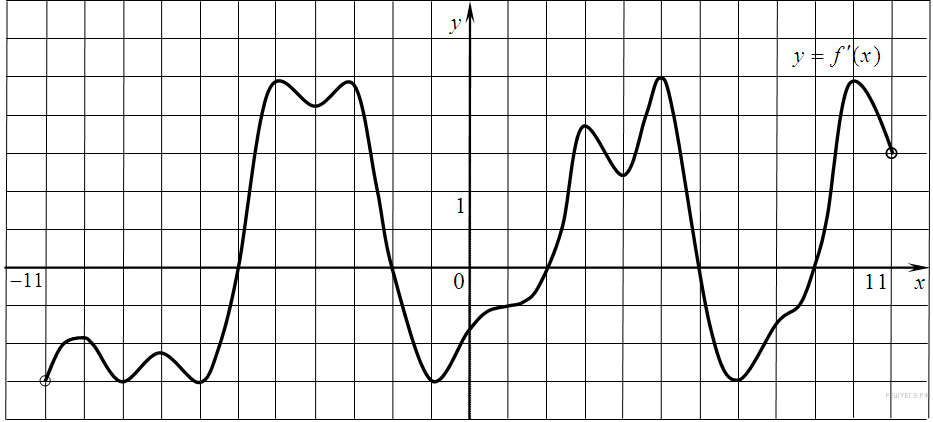 
На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].
| 4. |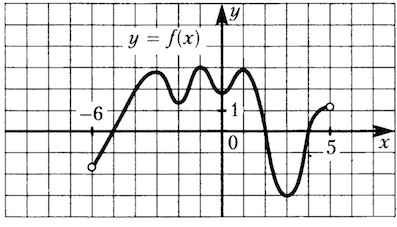 
На рисунке изображен график функции у = f (x), определенной на интервале (-6; 5). Найдите сумму точек экстремума функции
f (x).
|
| 2. | 
На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].
| 5. |
На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
|
| 3. |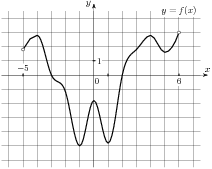 
На рисунке изображен график функции у = f (x), определенной на интервале
(-5; 6). Найдите сумму точек экстремума функции f(x).
| 6. |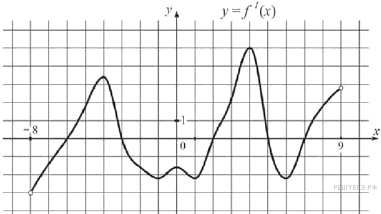 
На рисунке изображён график производной функции определенной на интервале (−8; 9). Найдите количество точек минимума у = f (x), функции принадлежащих отрезку [−4; 8].
|
Задание: Выполните задание по чертежу:
|
|
|
| 7. | 
На рисунке изображен график производной функции f(x), определенной на интервале
(−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
| 10. | 
На рисунке изображен график производной функции f(x), определенной на интервале
(−11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
|
| 8. | 
На рисунке изображен график производной функции f(x), определенной на интервале
(−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
| 11. | 
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
|
| 9. | 
На рисунке изображён график производной функции  и восемь точек на оси абсцисс: x1, x2, x3,…, x8. В ответе укажите точки, в которых функция убывает.
| 12. | 
На рисунке изображён график производной функции и восемь точек на оси абсцисс: x1, x2, x3,…, x8. В ответе укажите точки, в которых функция возрастает.
|
Задание: Найти точки экстремума и определить их характер:
| 13. | y=x 
| 16. | y=-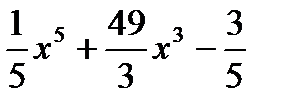 
|
| 14. | y=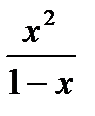 
| 17. | y=(x+1)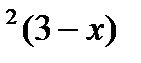 
|
| 15. | y=x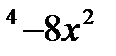 
| 18. | y=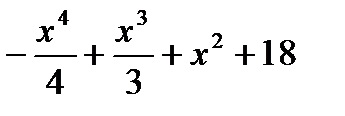 
|
Задание: Исследуйте на экстремум функцию:
| 19. |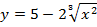 
| 22. |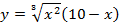 
|
| 20. | 
| 23. |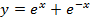 
|
| 21. |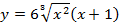 
| 24. |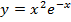 
|
Задание: Постройте график функции:
| 25. |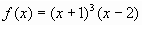 
| 28. |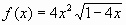 
|
| 26. |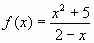 
| 29. | 
|
| 27. | 
| 30. |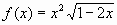 
|
Пояснения к работе:
Необходимые формулы:
