Задания на практическую работу
Все задания на практические работы составлены в 30 вариантах. Вариант практической работы соответствует номеру студента по списку в журнале.
Таблица вариантов практической работы
| № варианта | Номера задач | № варианта | Номера задач |
| 1 | 1,7,13,19,25 | 16 | 3,8,13,21,28 |
| 2 | 2,8,14,20,26 | 17 | 2,7,13,20,26 |
| 3 | 3,9,15,21,27 | 18 | 1,12,13,24,25 |
| 4 | 4,10,16,22,28 | 19 | 2,11,14,23,26 |
| 5 | 5,11,17,23,29 | 20 | 3,10,15,22,27 |
| 6 | 6,12,18,24,30 | 21 | 4,9,16,21,28 |
| 7 | 1,8,15,22,29 | 22 | 5,8,17,20,29 |
| 8 | 2,9,16,23,30 | 23 | 6,7,18,19,30 |
| 9 | 3,10,17,24,29 | 24 | 1,11,15,21,29 |
| 10 | 4,11,18,22,30 | 25 | 2,10,16,20,30 |
| 11 | 5,12,15,23,29 | 26 | 3,9,17,19,26 |
| 12 | 6,8,16,24,30 | 27 | 4,8,18,21,28 |
| 13 | 6,11,16,21,26 | 28 | 5,7,15,20,27 |
| 14 | 5,10,15,20,25 | 29 | 6,8,16,22,25 |
| 15 | 4,9,14,19,27 | 30 | 1,7,17,21,29 |
ПРАКТИЧЕСКАЯ РАБОТА №1
Тема: Вычисление производных сложных функций.
Цель работы: Корректировать знания, умения и навыки по теме: «Дифференциальное и интегральное исчисление».
Задание: Пользуясь формулами и правилами дифференцирования, найдите производные элементарных функций:
| 1. | а) 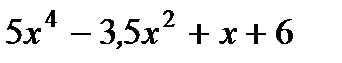 ;
б) ;
б)  ;
в) ;
в) 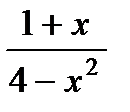 . .
| 4. | а) 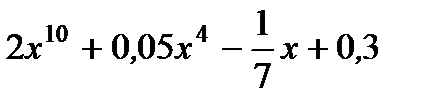 ;
б) ;
б)  ;
в) ;
в)  . .
|
| 2. | а)  ;
б) ;
б) 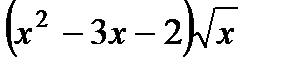 ;
в) ;
в)  . .
| 5. | а) 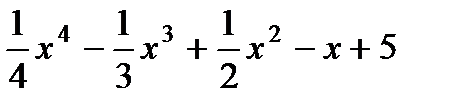 ;
б) ;
б) 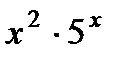 ;
в) ;
в) 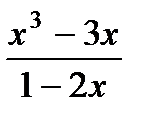 . .
|
| 3. | а) 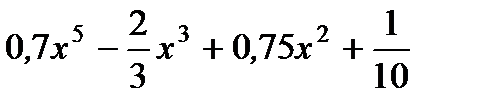 ;
б) ;
б) 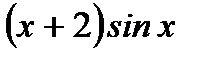 ;
в) ;
в) 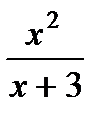 . .
| 6. | а)  ;
б) ;
б) 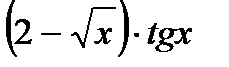 ;
в) ;
в) 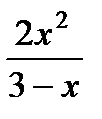 . .
|
Задание: Вычислить производную сложной функции:
| 7. | 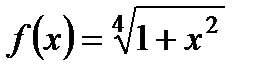 ; ;
| 10. | 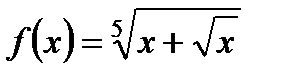 ; ;
|
| 8. |  ; ;
| 11. | 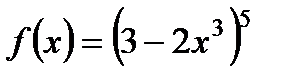 ; ;
|
| 9. |  ; ;
| 12. | 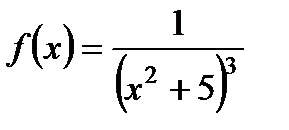 ; ;
|
Задание: Вычислите производную сложной функций:
| 13. | 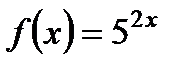 ; ;
| 16. | 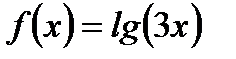 ; ;
|
| 14. | 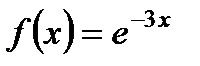 ; ;
| 17. | 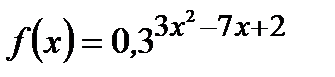 ; ;
|
| 15. |  ; ;
| 18. | 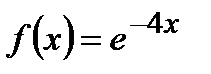 ; ;
|
Задание: Вычислите производную сложной функции:
| 19. | 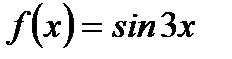 ; ;
| 22. |  ; ;
|
| 20. | 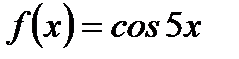 ; ;
| 23. | 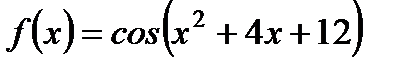 ; ;
|
| 21. |  ; ;
| 24. |  ; ;
|
Задание: Найдите угол, который образует с положительным лучом оси абсцисс касательная к графику функции:
| 25. |  в точке в точке 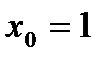 . .
| 28. | 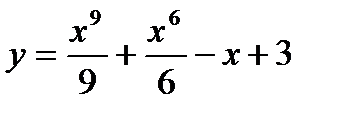 в точке в точке 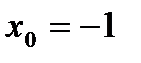 . .
|
| 26. |  в точке в точке 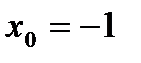 . .
| 29. | у = 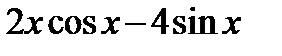 в точке х = 0. в точке х = 0.
|
| 27. | 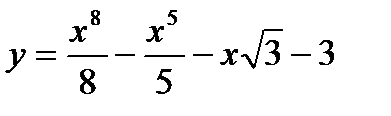 в точке в точке 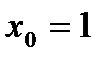 . .
| 30. | у = 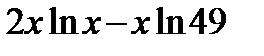 в точке х = 7. в точке х = 7.
|
Пояснения к работе:
Необходимые формулы:

Правило вычисления сложной функции.
Если y=f(u), где u=u(x), то есть y — сложная функция, то производная сложной функции находится по следующему правилу: y’=f'(u)·u'(x), то есть производную внешней функции f надо умножить на производную внутренней функции u.
Содержание отчета
1. Титульный лист в соответствии с СТП1.2-2005.
2. Цель работы
3. Задание
4. Выполненная практическая работа в соответствии с заданием
5. Ответы на контрольные вопросы
6. Вывод
Контрольные вопросы:
1. Дайте определение производной функции.
2. Дайте определение сложной функции.
3. Напишите основные формулы дифференцирования.
4. Запишите правило нахождения производной сложной функции.
5. В чем заключается геометрический и механический смысл производной.
ПРАКТИЧЕСКАЯ РАБОТА №2
Тема: Вычисление простейших определенных интегралов.
Цель работы: Корректировать знания, умения и навыки по теме: «Дифференциальное и интегральное исчисление».
Задание: Вычислить определенный интеграл
| 1. | 
| 4. | 
|
| 2. | 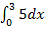
| 5. | 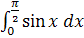
|
| 3. | 
| 6. | 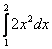
|
Задание: Вычислить определенный интеграл:
| 7. | 
| 10. | 
|
| 8. | 
| 11. | 
|
| 9. | 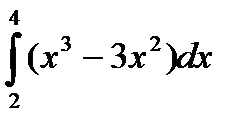
| 12. | 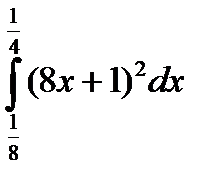
|
Задание: Вычислить определенный интеграл методом непосредственного интегрирования:
| 13. | 
| 16. | 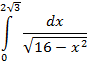
|
| 14. | 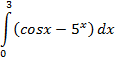
| 17. | 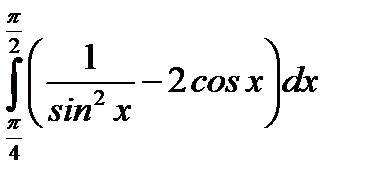
|
| 15. | 
| 18. | 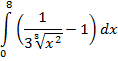
|
Задание: Вычислить интеграл способом подстановки (замены переменной):
| 19. | 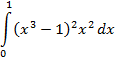
| 22. | 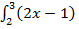 3 dx 3 dx
|
| 20. | 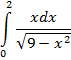
| 23. | 
|
| 21. | 
| 24. | 
|
Задание: Вычислить интеграл методом интегрирования по частям:
| 25. | 
| 28. | 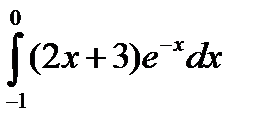
|
| 26. | 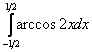
| 29. | 
|
| 27. | 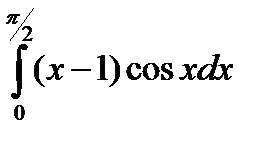
| 30. | 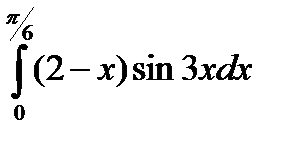
|
Пояснения к работе:
Необходимые формулы:
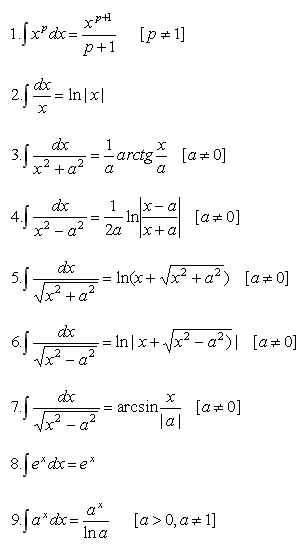
Интегрирование произведения (функции) на постоянную: 
 2020-09-24
2020-09-24 233
233







