Методы теплового моделирования

Метод изотермических элементов (метод сосредоточенных параметров) заключается в следующем: моделируемый объект разбивается на отдельные дискретные элементы таким образом, что температуру каждого элемента в некотором приближении можно считать однородной и изменяющейся только со временем. Эти элементы называются узлами. Каждый узел состоит из одной или нескольких поверхностей с заданными коэффициентами поглощения солнечного излучения A_S и степенями черноты e, описывающими их радиационные свойства.

Математическая модель объекта строится как система уравнений теплового баланса для каждого узла и включает тепловые потоки к узлу от лучистого и кондуктивного теплообмена его с другими узлами, потоки от тепловыделяющего оборудования, нагревателей системы терморегулирования и от внешнего окружения (Земли и Солнца). Так как конвективный теплообмен в орбитальных условиях отсутствует, то система дифференциальных уравнений, описывающая тепловую математическую модель объекта, имеет вид

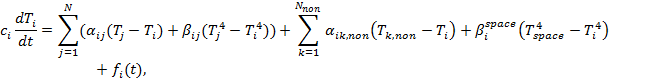
где t – время; N – число узлов; i – номер узла; 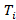,  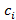 – температура и теплоемкость i-го узла; a_ij, b_ij – термические проводимости и коэффициенты лучистой термической связи между i-м и j-м узлами соответственно; T_k,non­, N_non, a_ik,non – температуры немоделируемых объектов, их количество и кондуктивные связи с расчетными узлами; T_space – температура открытого космоса;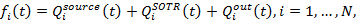 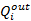 – внешние тепловые потоки от Земли и Солнца, поглощенные поверхностью i-го узла;  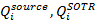– тепловые потоки к i-му узлу от тепловыделяющего оборудования и СОТР КА.

Так как основные законы лучистого теплообмена справедливы для замкнутой системы поверхностей, в математическую модель введен дополнительный нерасчетный узел «космос» с фиксированной температурой T_space, представляющий собой сферу с абсолютно черной внутренней поверхностью, которая содержит геометрическую модель КА.

Очень многие теплоэнергетические задачи теоретического характера сводятся к решению дифференциальных уравнений. Универсальным численным методом решения дифференциальных уравнений и их систем является разностный метод, называемый также методом конечных разностей или методом сеток [4]. Сущность этого метода заключается в том, что в области изменения переменных величин вводят некоторую сетку, а все производные, входящие в дифференциальные уравнения и условия однозначности, заменяют алгебраическими комбинациями от значений функции в узлах сетки. Решая полученную в результате такой замены систему алгебраических уравнений, называемую разностными уравнениями или разностной схемой, находят приближенные значения функции в узлах сетки. Таблица этих значений и принимается за решение исходной задачи.

Рассмотрим пример построения разностной схемы для дифференциального уравнения первого порядка вида

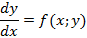
Заменим область непрерывного изменения аргумента дискретным множеством точек (вводим сетку)

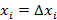
где ∆x – шаг сетки. Производную в уравнении заменим отношением конечных разностей и получаем разностное уравнение вида

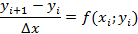
или

С помощью соотношения можно последовательно найти все значения y_i, и таким образом получить решение поставленной задачи. Следует отметить, что для одного и того же дифференциального уравнения могут быть построены различные разностные схемы. Например, изначальное уравнение может быть аппроксимировано разностным уравнением вида

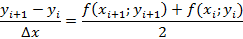
Замена исходного дифференциального уравнения разностным приводит к появлению погрешности численного метода, связанной с погрешностью аппроксимации. Для характеристики качества аппроксимации используют понятие ее порядка. Аппроксимация имеет порядок p, если ее погрешность, обусловленная заменой дифференциального уравнения разностным, пропорциональна шагу сетки в степени p.

Чем выше порядок аппроксимации, тем меньше при той же сетке погрешность, обусловленная заменой дифференциального уравнения разностным. Однако при этом существенно усложняется и разностная схема, поэтому разностные схемы высокого порядка (p >2) используются редко.

Наиболее часто для двумерных задач применяется прямоугольная сетка, узлы которой лежат на пересечении прямых, параллельных координатным осям (рис. 4.4), а для трехмерных – сетка из прямоугольных параллелепипедов, узлы которой лежат на пересечении плоскостей, параллельных координатным осям (рис. 4.5). Если область исследования является кругом, цилиндром или шаром, то обычно переходят к полярной, цилиндрической или сферической системе координат, соответственно меняется и вид сетки.

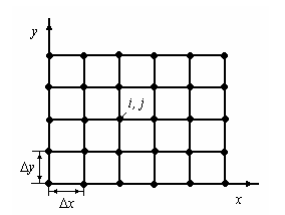
Рисунок 4.4 Прямоугольная сетка для двумерной задачи

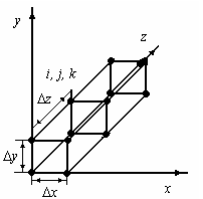
Рисунок 4.5 Сетка из прямоугольных параллелепипедов для трехмерной задачи

Одна из независимых переменных может иметь смысл времени τ. Совокупность узлов сетки с параметрами, принадлежащими одному моменту времени, называют слоем. В дальнейшем из всей совокупности узлов выделяют узлы внутренние и граничные. Значения искомой функции во внутренних узлах находят в результате решения системы разностных уравнений, а в граничных узлах определяют из граничных условий.

При записи разностного уравнения для какого-либо узла используют значения функции в узлах, лежащих в окрестности рассматриваемого. Конфигурацию этих узлов называют шаблоном разностной схемы.

Ещё один метод теплового моделирования - метод конечных элементов (МКЭ). Это численный метод решения дифференциальных уравнений, широко используемый в различных областях техники.

Основная идея МКЭ состоит в том, что любую непрерывную в некоторой области величину (например, внутреннее усилие в фундаментной балке, перемещение в плите перекрытия и т.п.) можно аппроксимировать дискретной моделью, которая создается из множества кусочно-непрерывных функций, определенных в конечном числе подобластей (элементов). Обычно такими функциями являются полиномы – линейные, квадратичные, кубичные и т.д. Кусочно-непрерывные функции строятся с помощью значений непрерывной величины в точках соединения элементов (в узлах) [6].

Таким образом, чтобы определить неизвестную непрерывную величину, нужно определить ее значения в узлах.

Основные этапы создания дискретной модели неизвестной величины следующие:

1. В исследуемой области задается конечное число точек (узлов).

2. Значения непрерывной величины в каждом узле считаются неизвестными, они должны быть определены.

3. Исследуемая область разбивается на конечное число подобластей (элементов), имеющих общие точки (узлы).

4. Непрерывная величина в каждом элементе аппроксимируется полиномом, который определяется с помощью узловых значений этой величины: для каждого элемента определяется свой полином, но его коэффициенты подбираются так, чтобы сохранялась непрерывность величины на каждой границе элемента.

Если неизвестная непрерывная величина ϕ определена в двух- или трехмерной области, аппроксимирующими являются функции от х и у или от х, у и z соответственно. Двумерная область разбивается обычно на элементы в форме треугольника или четырехугольника, трехмерная область – на элементы в форме тетраэдра или параллелепипеда. Аппроксимирующие функции изображаются в таком случае плоскими (рис. 4.6а) или криволинейными (рис. 4.6б) поверхностями (двумерная область).

Рисунок 4.6 Аппроксимирующие функции

Из сказанного выше следует, что основными преимуществами МКЭ являются следующие:

1. Возможность исследовать тела (конструкции), составленные из нескольких материалов (так как свойства материалов соседних элементов могут быть разными).

2. Возможность исследовать области (конструкции) любой формы (так как криволинейная область аппроксимируется прямолинейными элементами или точно описывается криволинейными элементами).

3. Возможность учета различных граничных условий: с разрывной нагрузкой, смешанных.

4. Возможность составления общих методик и программ для решения различных по физике задач одного определенного вида (например, программа осесимметричной задачи о распространении тепла может быть использована для решения любой задачи данного типа: о распределении напряжений в осесимметричной конструкции и т.п.).

Метод конечных объёмов — численный метод интегрирования систем дифференциальных уравнений в частных производных.

Основные положения МКО удобно излагать, рассматривая «стандартное» уравнение баланса некой величины φ в контрольном объеме Ω, ограниченном поверхностью S = ∑S_k с внешней нормалью :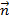

Здесь 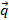 – вектор плотности потока величины φ, включающий конвективную и диффузионную составляющие, Q – плотность распределения объемных источников,  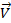– вектор скорости, ρ – плотность среды, α – коэффициент диффузии. В качестве φ может фигурировать, например, внутренняя энергия текущей среды, концентрация примеси, кинетическая энергия турбулентности и т.д. В пределе, при стягивании объема в точку, можно на основании формулы Остроградского-Гаусса переписать это уравнение в дифференциальной форме: 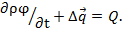Отметим, что последняя, в силу более частого использования в литературе, иногда считается первичной, а интегральная формулировка закона сохранения «выводится» из дифференциальной путем интегрирования по объему.

Согласно МКО пространственная дискретизация задачи осуществляется путем разбиения расчетной области на небольшие соприкасающиеся объемы, для каждого из которых записывается балансовое соотношение (рис. 4.7). Внутри каждого контрольного объема находится одна (и только одна) точка «привязки» искомого сеточного решения [7]. В большинстве разработок, ориентированных на решение трехмерных задач для областей сложной геометрии, в качестве контрольного объема используются ячейки расчетной сетки: узлы сетки располагаются в вершинах многогранника (для структурированных сеток – гексаэдра, см. рис.ниже), сеточные линии идут вдоль его ребер, а значения искомых величин приписываются геометрическому центру ячейки. Альтернативные варианты (например, построение контрольного объема вокруг узла сетки или введение различных контрольных объемов для разных переменных) встречаются реже и рассматриваться не будут.

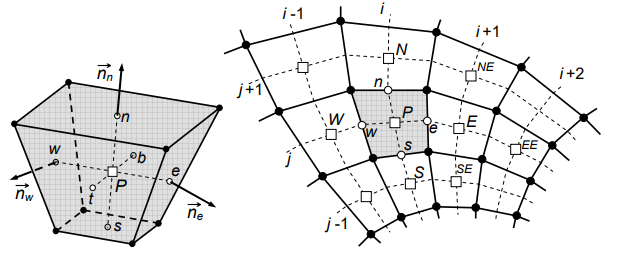
Рисунок 4.7 Структурированная сетка контрольных объемов с «привязкой» переменных к центру ячеек

 • – узел сетки, … – центр ячейки, о – центр грани.

Для получения дискретного аналога балансового уравнения в выбранной ячейке необходимо вычислить интегралы, входящие в него, используя какие-либо квадратурные формулы. При этом крайне важно, чтобы для соприкасающихся ячеек поверхностный интеграл по их общей грани S_k вычислялся идентично. Последнее требование, легко реализуемое при составлении компьютерной программы, обеспечивает консервативность численной схемы, т.е. точное (в рамках принятого способа вычисления интегралов) соблюдение баланса φ согласно уравнению баланса для всей области течения. Это свойство МКО выгодно отличает его от МКР и МКЭ, в которых реализация строгой консервативности схемы является скорее исключением, чем правилом.

На границе рассматриваемой области происходит взаимодействие с окружающей средой, которое должно быть описано граничными условиями.

Три наиболее важных типа граничных условий: граничное условие первого рода (условие Дирихле); граничное условие второго рода (условие Неймана); граничное условие третьего рода (условие Робена) [8].

Краевая задача с граничными условиями первого рода (задача Дирихле). Требуется найти решение уравнения в некоторой области пространства, которое принимает на границе области заданные значения. В качестве примера можно привести задачу о нахождении стационарного распределения температуры внутри области, если задана температура на границе этой области. Другой пример: найти распределение потенциала внутри области, если известен потенциал на границе.

Краевая задача с граничным условием второго рода (задача Неймана). Требуется найти решение уравнения в некоторой области пространства, на границе которой задана внешняя нормальная производная (которая пропорциональна втекающему потоку). Это общая задача и для теплопроводности, и для электростатики, если на границе задан поток (электронов, тепла и т.д.) [9].

Краевая задача с граничным условием третьего рода. Требуется найти такое решение уравнения в некоторой области пространства, которое удовлетворяет на границе условию вида:

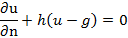
где h - заданная константа, a g - заданная функция, которая, вообще говоря, меняется вдоль границы.

Теперь рассмотрим эти условия на следующем примере: пусть рассматриваемый объект – это твердое тело, обменивающееся теплотой с окружающей средой (рис. 4.8). Требуется найти температурное поле t (x, y, z, τ) в объекте.

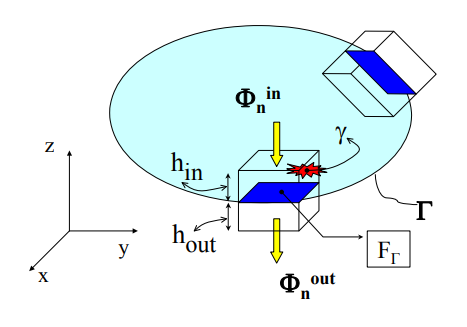
Рисунок 4.8 Рассматриваемое в примере твердое тело

 

Математическая формулировка этой задачи состоит из дифференциального уравнения теплопроводности:

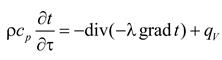
и описания теплового взаимодействия с окружающей средой, которое предстоит составить.

Граничное условие первого рода (условие Дирихле). С чисто математической точки зрения, было бы достаточно положить температуру поверхности тела равной некоторой заданной (известной до решения задачи) функции tГ от координат точек на поверхности и от времени:

В простейшем случае это может быть некоторая постоянная температура:

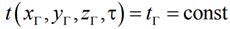
Однако пока остается неясным, как осуществить такое условие для реального объекта, в лабораторных или промышленных установках.

Граничное условие второго рода (условие Неймана). Пусть описание некоторой задачи на вербальном уровне выглядит так: твердое тело обогревается снаружи мощным потоком высокотемпературного теплового излучения q_R. Соответствующая математическая формулировка:

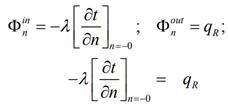
где q_R – заданная величина теплового потока на поверхности, возможно, функция времени и координат точек на поверхности; 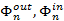 – плотность потоков по обеим сторонам границы раздела. Задав плотность потока, мы фактически задаем градиент температуры на поверхности: n означает внешнюю нормаль, а запись n = –0 подчеркивает, что величины вычисляются внутри объекта бесконечно близко к его поверхности.

Граничное условие третьего рода (условие смешанного типа, условие Роббина). На практике граница Г чаще всего отделяет элементы конструкций (твердые тела) от обтекающих их потоков газов или жидкостей (теплоносителей). В свое время Исаак Ньютон экспериментально, с помощью специально изготовленных им термометров, исследовал охлаждение первоначально сильно нагретых металлических тел в воздухе. Он обнаружил, что скорость падения температуры пропорциональна самой температуре тела:

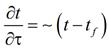
В современной формулировке закон охлаждения Ньютона записывается следующим образом:

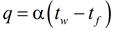
Где  – температурный напор, разность температур стенки (поверхности) и окружающей среды.

Ясно, почему в этом уравнении должен фигурировать температурный напор: при одинаковых температурах поверхности и окружающей среды никакого теплового потока не возникает. Из общих соображений понятно также, что если теплоотвод пропорционален разности температур, то и скорость понижения температуры тела будет пропорциональна этой разности температур.

Пусть охлаждение твердого тела в среде с температурой t_f происходит по закону Ньютона–Рихмана. Соответствующая математическая формулировка граничного условия третьего рода получается следующим образом:

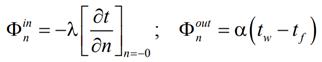
и окончательно:

 

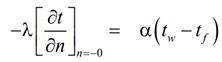
При задании граничных условий третьего рода устанавливается связь между неизвестными заранее температурой и градиентом температуры на поверхности. Вариация параметров α и t_f предоставляет широкие возможности регулирования условий охлаждения (или нагрева) тел. Если обеспечить очень высокое значение коэффициента теплоотдачи α, например, посредством интенсивного перемешивания жидкости, то фактически будет реализовано условие Дирихле, поскольку из последнего уравнения следует, что t_w →t_f при α → ∞ и конечном значении теплового потока.

Если задать очень малое значение α, то получится условие адиабатической поверхности, т.е. частный случай условия Неймана при нулевом тепловом потоке на поверхности. Если t_f>>t_w, то фактически опять будет задано условие Неймана с подводимым к поверхности тепловым потоком q ≈ αt_f.