2020-09-24
117
Рассмотрим теперь интегрирование функций, содержащих радикалы. Не от всякой иррациональной функции интеграл выражается через элементарные функции. Однако в наиболее простых случаях, когда над радикалами выполняются рациональные действия, это удается сделать. Необходимо отметить, что все такие иррациональные функции интегрируются посредством их рационализации, то есть избавления от корней.
1. Пусть дан интеграл
,
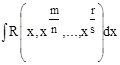где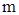 
, 
,…, 
, 
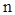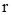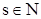. Найдем общий знаменатель дробей 
,…, 
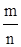. Пусть это число 
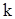. Сделаем подстановку 
, 
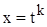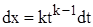. В этом случае все дробные степени становятся целыми и подынтегральная функция становится рациональной относительно 
.
2. Рассмотрим общий случай подобных интегралов:
,
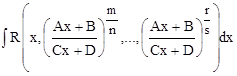где , ,…, , .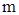
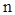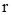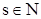Чтобы получить рациональную функцию, находят общий знаменатель дробей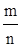 
,…, (обозначим его 
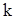) и делают замену переменной 
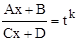. В этом случае
.
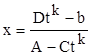
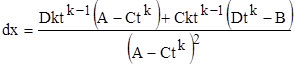Очевидно, есл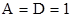и 
и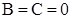 
, то случай 2 переходит в случай 1. Кроме того, необходимо иметь в виду, что в обоих случаях основания всех степеней должны быть одинаковы: в первом случае 
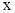, во втором – 
.
|
|
|
Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
Рассмотри снова интегралы, содержащие квадратный трехчлен:
.
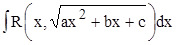Выделив полный квадрат под корнем, получим один из трех интегралов: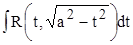 
, 
, 
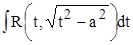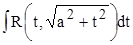. Все они вычисляются с помощью тригонометрических подстановок.
1. 
.
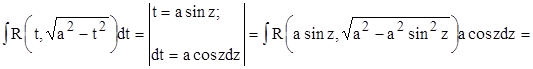
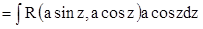2. 
.
3. 
.
Во всех трех случаях после проведенных подстановок интегралы пришли к виду, рассмотренному в п. 2.
