Контрольная работа
Дисциплина:
«Высшая математика»
Тема:
«Универсальная тригонометрическая подстановка»
Универсальная тригонометрическая подстановка
Рассмотрим интегрирование выражений полностью зависящих от тригонометрических функций, над которыми выполняются лишь арифметические операции. Такие выражения называются рациональными функциями от тригонометрических функций и в данном случае обозначаются  . Например,
. Например,
 ,
, 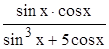 ,
,  .
.
В то же время функция 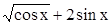 рациональной не является.
рациональной не является.
Теорема. Интеграл вида 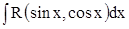 с помощью подстановки
с помощью подстановки 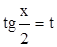 преобразуется в интеграл от рациональной дроби.
преобразуется в интеграл от рациональной дроби.
Для доказательства выразим  ,
, 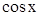 и
и 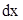 через
через  :
:
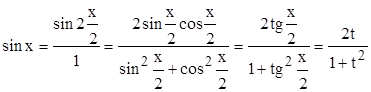 ;
;
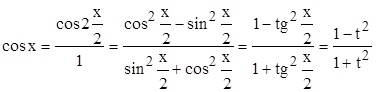 ;
;
 .
.
В результате проведенных преобразований  ,
, 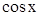 и
и 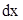 превратились в рациональные дроби от
превратились в рациональные дроби от  . Подставляя их в исходный интеграл, получаем:
. Подставляя их в исходный интеграл, получаем:
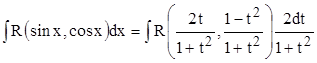 .
.
В данном выражении рациональные дроби подставлены в рациональную функцию. Так как над ними выполняются лишь арифметические операции, то в результате получается также рациональная дробь. Итак, рациональную функцию от тригонометрических функций можно проинтегрировать, превратив ее в рациональную дробь.
Подстановка
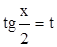 ,
, 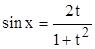 ,
,  ,
, 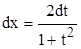
называется универсальной тригонометрической подстановкой.
Частные случаи интегрирования выражений, содержащих тригонометрические функции
Рассмотренная в п. 11 универсальная тригонометрическая подстановка позволяет вычислить любой интеграл от функции вида  . Однако на практике она часто приводит к слишком сложным рациональным функциям, интегрирование которых представляет значительную трудность. Есть целый ряд интегралов от тригонометрических функций, которые можно вычислить значительно проще.
. Однако на практике она часто приводит к слишком сложным рациональным функциям, интегрирование которых представляет значительную трудность. Есть целый ряд интегралов от тригонометрических функций, которые можно вычислить значительно проще.
1. Интегралы типа  удобно вычислять с помощью подстановки
удобно вычислять с помощью подстановки 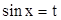 . Тогда
. Тогда 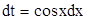 и получаем простой интеграл
и получаем простой интеграл 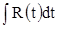 .
.
2. Интегралы типа 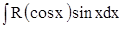 удобно вычислять с помощью подстановки
удобно вычислять с помощью подстановки  . Тогда
. Тогда  и интеграл приводится к виду
и интеграл приводится к виду 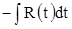 .
.
3. Если подынтегральная функция зависит только от 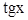 (
(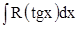 ), то удобна замена
), то удобна замена  . В этом случае
. В этом случае 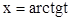 и
и 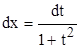 . В результате получаем
. В результате получаем 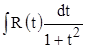 .
.
4. Если подынтегральная функция является рациональной относительно четных степеней  и
и 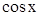 , то есть
, то есть 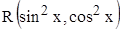 , то в этом случае также удобна замена
, то в этом случае также удобна замена  . При этом:
. При этом:
 ;
;
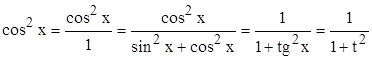 ;
;
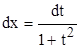 .
.
Данная подстановка в этом случае дает более простую рациональную дробь, чем с использованием универсальной тригонометрической подстановки.
Пусть дан интеграл  , где
, где 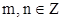 и при этом хотя бы одно из этих чисел нечетное. Допустим, что
и при этом хотя бы одно из этих чисел нечетное. Допустим, что 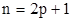 . Тогда
. Тогда
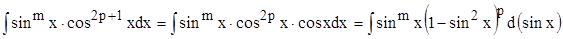 .
.
Далее делается замена 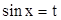 , и получаем
, и получаем 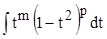 .
.
6. Пусть дан интеграл 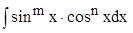 , где
, где 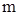 и
и 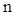 неотрицательные и четные. Положим, что
неотрицательные и четные. Положим, что  ,
, 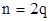 . Тогда
. Тогда
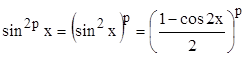 ;
; 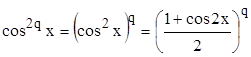 .
.
Данная замена позволяет в два раза понизить степень тригонометрических функций. Раскрывая скобки в интеграле 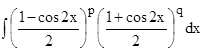 , получаем снова случаи 5 или 6.
, получаем снова случаи 5 или 6.
7. Пусть дан  , где
, где 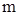 и
и  – четные и хотя бы одно из этих чисел отрицательно. Тогда удобна та же замена, что и в случае 4.
– четные и хотя бы одно из этих чисел отрицательно. Тогда удобна та же замена, что и в случае 4.
8. В случае 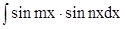 используется тригонометрическая формула
используется тригонометрическая формула

и интеграл превращается в два табличных интеграла.
9. В случае 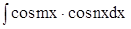 используется тригонометрическая формула
используется тригонометрическая формула
 .
.
10. В случае 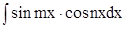 используется тригонометрическая формула
используется тригонометрическая формула
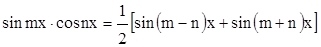 .
.
3. Тригонометрические подстановки для интегралов вида 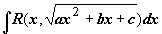
Рассмотрим тригонометрические подстановки для вычисления таких интегралов, которые сводят подынтегральную функцию к функции, рационально зависящей от  и
и 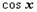 . Вначале выполняется выделение полного квадрата в трёхчлене (и соответствующей линейной замены переменной), в результате этого интеграл сводится, в зависимости от знаков
. Вначале выполняется выделение полного квадрата в трёхчлене (и соответствующей линейной замены переменной), в результате этого интеграл сводится, в зависимости от знаков 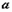 и дискриминанта трёхчлена, к интегралу одного из следующих трёх видов:
и дискриминанта трёхчлена, к интегралу одного из следующих трёх видов:
 ,
,  ,
, 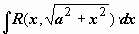 .
.
Следующий шаг:
1) 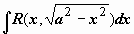 рационализируется подстановкой x = a sin t (или x = a cos t). Замена переменной в неопределённом интеграле.
рационализируется подстановкой x = a sin t (или x = a cos t). Замена переменной в неопределённом интеграле.
2)  рационализируется подстановкой
рационализируется подстановкой 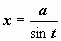 (или
(или 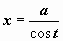 , или
, или 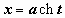 ).
).
3) 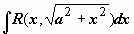 рационализируется подстановкой x = a tg t (или x = a ctg t, или x = a sh t).
рационализируется подстановкой x = a tg t (или x = a ctg t, или x = a sh t).
 Пример 1.
Пример 1. 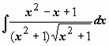 . Интеграл вида
. Интеграл вида  , из возможных подстановок наиболее удобной оказывается x = ctg t.
, из возможных подстановок наиболее удобной оказывается x = ctg t.
 ,
,
поэтому 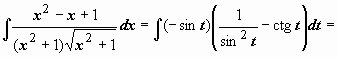
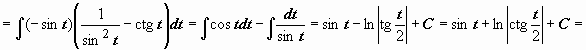
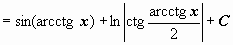
или
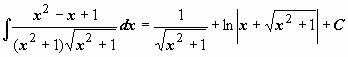 .
.
 Пример 2.
Пример 2.
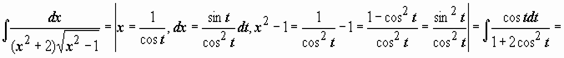

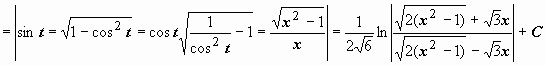
 2020-09-24
2020-09-24 1276
1276