2020-09-24
282
Расчетная схема экспериментального сосуда показана на рис.1, а. Для определения меридиональных, кольцевых и радиальных напряжений 
от внутреннего давления p используются следующие уравнения:
уравнение равновесия элемента
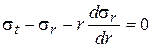. (1)
Данное уравнение выражает условие равновесия выделенного элемента оболочки (рис.1, б) под действием нагрузок в направлении радиуса обечайки;
уравнение совместности деформаций
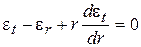. (2)
Уравнение (2) выражает связь между относительными кольцевыми и радиальными деформациями данного элемента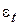 
и 
;
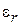уравнение равновесия зоны
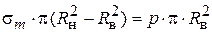. (3)
В соответствии с уравнением (3) действие растягивающих сил в меридиональном направлении уравновешивается внутренними меридиональными силами (напряжением 
).
 |
Рис.1. Расчетная схема экспериментального сосуда (а), схема распределения
напряжений в элементе толстостенной оболочки (б) и эпюры напряжений
от внутреннего давления (в)
Согласно обобщенному закону Гука относительные деформаци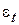и 
и 
связаны с напряжениям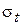и 
, 
и 
следующим образом:
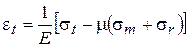, (4)
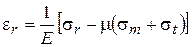. (5)
Выражения для 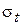и , получаемые совместным решением уравнений (1), (2), (4), (5), имеют вид
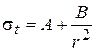, (6)
. (7)
Константы интегрирования A и B в выражениях (6), (7) определяются из граничных условий на внутренней и наружной поверхностях оболочки:
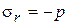при 
,
при 
.
С учетом (3) окончательные выражения для меридиональных, кольцевых и радиальных напряжений записываются в виде
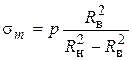, (8)
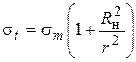, (9)
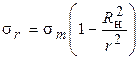. (10)
Приведенные формулы известны как формулы Ламе (по имени французского математика и инженера Габриеля Ламе, работавшего в Петербургской академии наук и впервые решившего данную задачу в 1830 – 1833 гг.).
Эпюры напряжений, построенные по формулам Ламе, показаны на рис.1, в.
