Теоретические сведения

Занятие №1

Раздел 1 Элементы теории вероятностей

Тема 1.1 Основные понятия теории вероятностей

- Предмет теории вероятностей.

- Испытание и событие.

- Виды событий.

- Виды случайных событий.

- Операции над событиями.

Цель: рассмотреть основные понятия теории вероятностей.

Рекомендуемая литература:

1 Валуцэ, И. И. Математика для техникумов на базе средней школы: учеб. пособие / И. И. Валуцэ, Г. Д. Дилигул. – М.: Наука, 1989. – 2-е изд., перераб. и доп.- 576 с.: ил.

2 Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие для среднего профессионального образования / В. Е. Гмурман. — 11-е изд., перераб. и доп. — Москва: Издательство Юрайт, 2020. — 406 с. — (Профессиональное образование). — ISBN 978-5-534-08569-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/451168, c. 157-158

Ход занятия:

1) Ознакомиться с теоретическим материалом по теме.

Теоретические сведения

Теория вероятностей – это раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.

Примеры событий:

– попадание в цель при выстреле из орудия (опыт — произведение выстрела; событие — попадание в цель);

– выпадение двух гербов при трёхкратном бросании монеты (опыт — трёхкратное бросание монеты; событие — выпадение двух гербов);

– появление ошибки измерения в заданных пределах при измерении дальности до цели (опыт — измерение дальности; событие — ошибка измерения).

Можно привести бесчисленное множество подобных примеров. События обозначаются заглавными буквами латинского алфавита А, В, С и т.д.

Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие А — выпадение трех очков на первой игральной кости, событие В — выпадение трех очков на второй кости. А и В — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие А — наудачу взятая коробка окажется с обувью черного цвета, событие В — коробка окажется с обувью коричневого цвета, А и В — несовместные события.

Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.

Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.

Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.

События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.

Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера. А — появление красного шара при одном извлечении, В — появление белого шара, С — появление шара с номером. События образуют полную группу совместных событий.

Введем понятие противоположного, или дополнительного, события. Под противоположным событием понимается событие 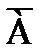, которое обязательно должно произойти, если не наступило некоторое событие 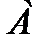. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие 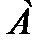, либо бракованным — событие .

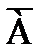При разработке аппарата и методики исследования случайных событий в теории вероятностей очень важным является понятие суммы и произведения событий.

Суммой, или объединением нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

Сумма 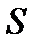событий А, В, С,…,N обозначается так:

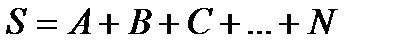Например, если событие 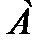есть попадание в цель при первом выстреле, событие В — при втором, то событие 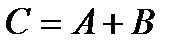есть попадание в цель вообще, безразлично, при каком выстреле — первом, втором или при обоих вместе.

Произведением, или пересечением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Произведение 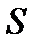событий А, В, С,…,N обозначается так:

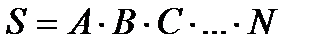Например, если событие 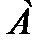есть попадание в цель при первом выстреле, событие В — при втором, то событие 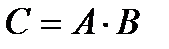состоит в том, что в цель попали при обоих выстрелах.

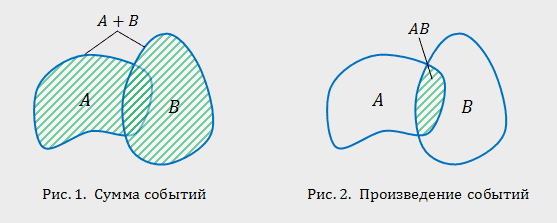
Понятия суммы и произведения событий имеют наглядную геометрическую интерпретацию. Пусть событие 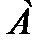состоит в попадании точки в область, событие В — в попадании в область, тогда событие 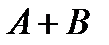состоит в попадании точки в область, заштрихованную на рис. 1, и событие 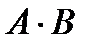— в попадании точки в область, заштрихованную на рис. 2.