Лекция №4
Тема: «Дифференциальное исчисление»
Важнейшим понятием математического анализа является производная, которая определяет скорость изменения функции.
Дифференциальное исчисление – раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций.
Понятие производной
Пусть задана некоторая функция y = f(x).
Возьмем какое-нибудь значение х0 из области определения этой функции: х0 Є D(f). Соответствующее значение функции в этой точке будет равно y0 = f(x0).
Определение:
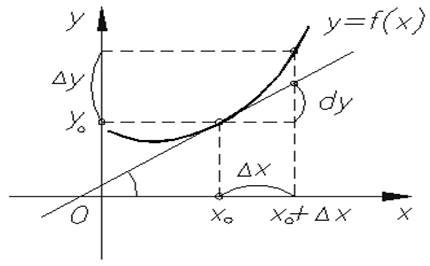
приращением аргумента х в точке х0 называется величина ∆х = х – х0 (разность между двумя значениями аргумента: новым и исходным)
Зададим аргументу xo приращение ∆х, тогда значение функции в новой точке х = х0+∆х будет равно f(х0 + ∆х).
Определение: приращением функции y = f(x)в точке х0 называется величина
∆у = у – у0 = f(х0 + ∆х) – f(х0)
Определение производной. Производной у'(х) от функции y = f(x)в точке х0 называется предел отношения приращения функции к приращению аргумента при ∆х→0, если он существует, то есть
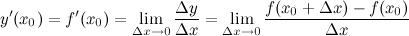
Геометрический смысл производной - значение производной функции y = f(x) в точке равно угловому коэффициенту касательной к графику данной функции в точке х0 : f '(х0) = tg 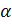 =k
=k
Задание: на чертеже обозначить угол 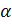 (см. угол, который выделен дугой)
(см. угол, который выделен дугой)
Если функция y = f(x) имеет производную в точке х0 (дифференцируема в точке), то она непрерывна в этой точке.
Функция y = f(x)имеет производную на интервале (а;b) (дифференцируема на этом интервале), если производная f '(х) существует в каждой точке этого интервала.
Операция нахождения производной функции называется дифференцированием этой функции.
Фактически производная функции показывает скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции – производная от пути по времени есть мгновенная скорость движения.
Пусть задан путь 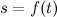 движения материальной точки. Скорость данной материальной точки в момент времени
движения материальной точки. Скорость данной материальной точки в момент времени 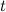 есть производная от пути
есть производная от пути  по времени
по времени 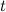 :
:
s | (t) = v(t)
Соответственно, вторая производная функции - скорость изменения скорости, т.е. ускорение.
s''(t) = a(t)
Формулы дифференцирования
Таблица производных
| (xp)' = pxp-1 | (sin x)' = cos x |
| x' = 1 | (cos x)' = - sin x |
(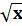 )' = )' = 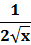
| (tgx)' = 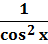
|
( )' = )' = 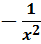
| (ctgx)' = 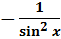
|
| C' = 0,где С - const | (arcsin x)' = 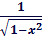
|
| (ex)'= ex | (arccos x)' = 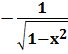
|
(ax)'= ax 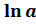
| (arctg x)' = 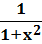
|
(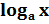 )' = )' = 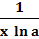
| (arcctg x)' = 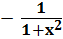
|
(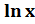 )' = )' = 
|
 2020-10-10
2020-10-10 168
168







