Схема взаимодействия комплекса физических процессов, протекающих при сварке и влияющих на качество получаемых сварных соединений, показана на рис. 12.13. Процессы отмечены номерами, а стрелками изображены связи между ними – явления, вызывающие влияние одного процесса на другой.

Рис. 12.13. Схема взаимодействия процессов при сварке: 1 – процессы в сварочном источнике питания; 2 – процессы в источнике энергии сварки, например, в сварочной дуге; 3 – протекание электрического тока через сварное соединение; 4 – распространение теплоты при нагреве и охлаждении; 5 – структурные и фазовые превращения, в том числе плавление и кристаллизация сварного шва; 6 – изменение свойств материала; 7 – диффузия примесей, механическое перемешивание материала сварного шва; 8 – образование сварочных деформаций и напряжений; 9 – повреждение или полное разрушение сварного соединения
Многие процессы оказывают взаимное влияние друг на друга, т. е. связи между ними являются двусторонними. Например, изменение температуры вызывает фазовые превращения в сварном шве и зоне его термического влияния. В свою очередь выделение и поглощение теплоты от превращений изменяет температуру.
Часто важность и влияние прямой и обратной связи несоизмеримы, тогда более слабой из них можно пренебречь. Например, расширение материала от нагрева является главной причиной сварочных деформаций и напряжений, а выделение теплоты при пластической деформации незначительно по сравнению с теплотой от сварочной дуги.
Схема на рис. 12.13 демонстрирует сложность совокупности процессов при сварке и многочисленность связывающих их явлений. Каждому способу сварки соответствует определенный список основных процессов, которые имеют наиболее важное значение для этого способа и требуют обязательного учета при его моделировании. Менее важные процессы могут быть учтены в граничных условиях при моделировании основных процессов.
Некоторые явления, возникающие при сварке (нагрев и охлаждение, действие агрессивных сред, деформации) могут присутствовать и в эксплуатационных нагрузках, т. е. действовать на готовую конструкцию, влияя на ее работоспособность.
Теория упругости и пластичности
Все рассмотренные ранее процессы энергомассопереноса можно представить себе как протекание некоторой идеальной жидкости через пористую среду. Поэтому их можно описать аналогичными уравнениями. Процесс деформирования твердого тела ближе к течению вязкой жидкости. В ней действует не только давление, но и внутреннее трение: при движении некоторого фрагмента вязкой среды он вовлекает в это движение смежные фрагменты не только впереди и позади, но и по бокам от своей траектории.
В связи с этим поле деформаций и напряжений в твердом теле нельзя описать распределением скалярной функции (потенциала). Это поле является векторным, и в каждой его точке необходимо указать три компоненты вектора - например, перемещения этой точки по трем координатным осям.
Поведение упругого материала описывает теория упругости. Согласно этой теории, между деформациями и напряжениями такого материала существует однозначная связь (не обязательно пропорциональная). Более сложное упругопластическое поведение материала описывает теория пластичности. Эти две теории лежат в основе дисциплины «сопротивление материалов».
Теория деформаций
Существует три вида движения твердого тела (рис. 12.14): поступательное, вращательное и деформационное (изменение расстояний между точками тела). Изменение линейных размеров называется линейной деформацией, а изменение угловых размеров - угловой.

Рис. 12.14. Схема перемещений и деформаций твердого тела
Всего в каждом элементарном объеме тела могут присутствовать три компоненты линейной деформации по трем осям и три компоненты угловой деформации. Для сокращения количества аналогичных формул используют тензорную форму записи:
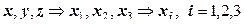 ;
;
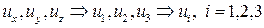 .
.
Компоненты линейной деформации выражают через изменения длины отрезков в теле (разности перемещений их концов):
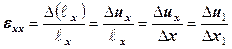 ;
;
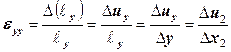 и т. д.
и т. д.
Общая формула:
 . (12.29)
. (12.29)
Компоненты угловой деформации выражают через разности перемещений концов отрезков, направленных по нормали к этим отрезкам:
 .
.
Это угол взаимного поворота двух перпендикулярных отрезков. При малых значениях перемещений формулу можно упростить:
 [рад];
[рад];
 .
.
Введя обозначение 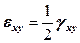 , получим единую формулу для малых линейных и угловых деформаций, которая включает в себя формулу (12.29), как частный случай:
, получим единую формулу для малых линейных и угловых деформаций, которая включает в себя формулу (12.29), как частный случай:
 . (12.30)
. (12.30)

Это средние деформации по длине отрезков 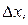 . Для бесконечно малой окрестности точки отношения превращаются в частные производные, поэтому деформации в точке тела
. Для бесконечно малой окрестности точки отношения превращаются в частные производные, поэтому деформации в точке тела
 . (12.31)
. (12.31)
Формулы (12.29-12.31) просты (устанавливают линейную зависимость деформаций от перемещений), но приводят к погрешности при поворотах тела как единого целого. По этим формулам поворот выглядит как сжатие. Рассмотрим изменение длины 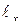 отрезка с учетом больших продольных и поперечных перемещений одного из его концов (рис. 12.15):
отрезка с учетом больших продольных и поперечных перемещений одного из его концов (рис. 12.15):


Рис. 12.15. Искажение деформации при повороте тела
Из рис. 12.15 видно, что в гибких стержнях и оболочках даже малых деформациях могут возникать большие перемещения (из  не следует, что
не следует, что 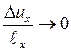 и
и 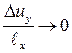 ).
).
Формула, исключающая ложные деформации от поворота тела или его фрагмента в пространстве:
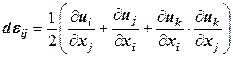 . (12.32)
. (12.32)
В этой формуле применена сокращенная тензорная запись скалярного произведения векторов, выражение 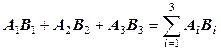 записывают как
записывают как 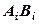 , пропуская знак суммы. О необходимости вычисления и суммирования произведений при всех значениях «слепого» индекса i сигнализирует его двукратное повторение в формуле. Традиционная запись последнего члена уравнения (12.32)
, пропуская знак суммы. О необходимости вычисления и суммирования произведений при всех значениях «слепого» индекса i сигнализирует его двукратное повторение в формуле. Традиционная запись последнего члена уравнения (12.32)
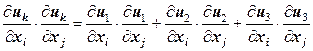 .
.
Для линейной деформации из (12.32) получаем
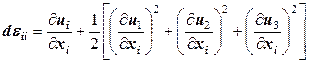 .
.
Формула (12.32) дает компоненты деформации в системе координат, связанной с волокнами материала. В результате перемещений точек эта система поворачивается в пространстве относительно исходной системы координат. Компоненты поворота, найденные по формулам
 (12.33)
(12.33)
позволяют рассчитать компоненты деформации в исходной системе координат.
Деформацию, измеренную по отношению к исходным размерам тела 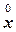 , называют деформацией Коши,
, называют деформацией Коши,
 , (12.34)
, (12.34)
а по отношению к размерам тела после его деформирования 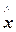 - деформацией Альманси:
- деформацией Альманси:
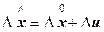 ,
,
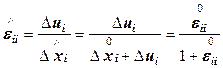 . (12.35)
. (12.35)
Истинные деформации, или деформации Генки, определяют по отношению к текущим размерам тела, меняющимся в процессе деформирования:
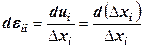 .
.
Для этого необходимо разбить процесс на бесконечно мелкие шаги и найти деформацию интегрированием от  до
до 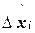 :
:
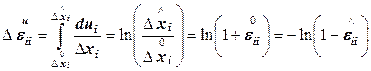 . (12.36)
. (12.36)
Различие между тремя видами деформации становится существенным при 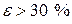 .
.
Деформации Коши и Альманси несимметричны при растяжении и сжатии. Если отрезок длиной  растянуть в два раза, то
растянуть в два раза, то 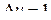 ,
, 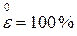 ,
,  , а
, а 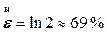 . Если тот же отрезок сжать в два раза, то
. Если тот же отрезок сжать в два раза, то 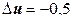 ,
,  ,
, 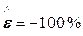 , а
, а  . Деформация Коши
. Деформация Коши  означает, что размер стал нулевым
означает, что размер стал нулевым  , а дальше размер меняет знак, «выворачивается наизнанку». Аналогично поведение деформации Альманси при
, а дальше размер меняет знак, «выворачивается наизнанку». Аналогично поведение деформации Альманси при  . Деформацию Генки называют истинной, поскольку она имеет одинаковые числовые значения при растяжении и сжатии в два раза и сохраняет физический смысл при любых значениях деформации:
. Деформацию Генки называют истинной, поскольку она имеет одинаковые числовые значения при растяжении и сжатии в два раза и сохраняет физический смысл при любых значениях деформации:  имеет место, когда тело вытягивается в длинную нить, а
имеет место, когда тело вытягивается в длинную нить, а 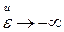 , когда тело расплющивается в тонкую пластину. Возможность пересчета любого из трех видов деформации в остальные показывает, что все они равноценны.
, когда тело расплющивается в тонкую пластину. Возможность пересчета любого из трех видов деформации в остальные показывает, что все они равноценны.
Совокупность компонент деформации называют тензором:
 . (12.37)
. (12.37)
Тензор – это вектор второго порядка, характеризуемый величиной и парой направлений (каждая компонента деформации связана с двумя осями, вдоль одной оси направлен отрезок, вдоль другой – перемещение конца отрезка). Закон парности касательных деформаций, являющийся следствием формул (12.31) и (12.32):
 (12.38)
(12.38)
сокращает число независимых компонент тензора до шести. Три параметра характеризуют ориентацию главных осей деформации в выбранной системе координат, а три других (инварианты) характеризуют деформированное состояние и не зависят от выбора системы координат.
Первый инвариант тензора 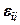 – относительное изменение объема
– относительное изменение объема 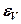 :
:
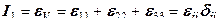 ,
,
где 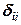 - символ Кронекера,
- символ Кронекера,  .
.
Шаровой тензор соответствует состоянию всестороннего равноосного растяжения или сжатия, при котором изменяется объем тела без изменения его формы:
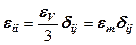 . (12.39)
. (12.39)
Найдя первый инвариант любого тензора, можно выделить из него шаровую составляющую (шаровой тензор):
 . (12.40)
. (12.40)
Девиатор тензора может быть найден путем вычитания из него шаровой составляющей. Девиатор деформации  характеризует только изменение формы тела, его шаровая составляющая нулевая:
характеризует только изменение формы тела, его шаровая составляющая нулевая:
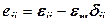 ; (12.41)
; (12.41)
 ; (12.42)
; (12.42)
 . (12.43)
. (12.43)
Компоненты тензора зависят от выбора осей. Если в системе координат  все угловые компоненты тензора становятся равными нулю и остаются только линейные деформации
все угловые компоненты тензора становятся равными нулю и остаются только линейные деформации
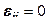 при
при 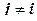 ,
,
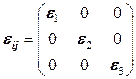 , (12.44)
, (12.44)
то такие оси и компоненты деформации называют главными:
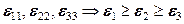 . (12.45)
. (12.45)
У шарового тензора все оси главные.
Угловые деформации при повороте осей на 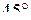 переходят в линейные, и наоборот:
переходят в линейные, и наоборот:  (рис. 12.16), поскольку при взаимном повороте двух осей (при угловой деформации) изменяется расстояние между парой точек, лежащих на этих осях (происходит линейная деформация отрезка, соединяющего эту пару точек).
(рис. 12.16), поскольку при взаимном повороте двух осей (при угловой деформации) изменяется расстояние между парой точек, лежащих на этих осях (происходит линейная деформация отрезка, соединяющего эту пару точек).
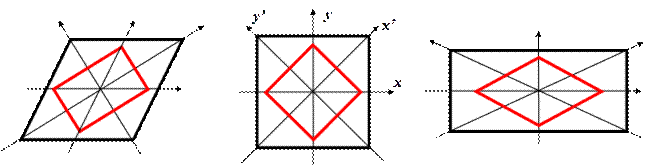
Рис. 12.16. Связь линейных и угловых деформаций
Всего тензор имеет шесть независимых параметров, в том числе три инварианта. Полный комплект инвариантов включает три параметра. Примеры таких комплектов:  ;
; 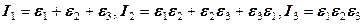 . Любые комбинации из инвариантов также являются инвариантами.
. Любые комбинации из инвариантов также являются инвариантами.
Главные деформации  – это корни кубического уравнения
– это корни кубического уравнения
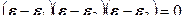 (12.46)
(12.46)
или
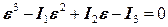 . (12.47)
. (12.47)
Способ нахождения главных компонент:
1) имеются формулы расчета инвариантов 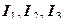 по компонентам произвольного тензора, например:
по компонентам произвольного тензора, например:
 ;
;
2) найдя инварианты, нужно составить и решить кубическое уравнение (12.47).
Один из важнейших инвариантов девиатора деформации – интенсивность деформации:
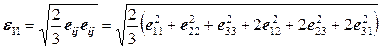 . (12.48)
. (12.48)
Любая деформация представляет собой изменение формы и размеров элементарного объема материала. Если в исходном состоянии этот объем имел форму сферы и радиус  , то после деформации он превращается в эллипсоид, осями симметрии которого являются главные оси деформации, а длина осей эллипсоида составляет
, то после деформации он превращается в эллипсоид, осями симметрии которого являются главные оси деформации, а длина осей эллипсоида составляет 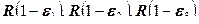 . Дальнейшую деформацию можно представить себе либо как растяжение и сдвиг этого эллипсоида (в результате каждый раз получается опять эллипсоид), либо как его вращение в пространстве с изменением длины главных осей.
. Дальнейшую деформацию можно представить себе либо как растяжение и сдвиг этого эллипсоида (в результате каждый раз получается опять эллипсоид), либо как его вращение в пространстве с изменением длины главных осей.
Первый инвариант деформации показывает изменение объема эллипсоида (независимо от формы и соотношения осей), второй - суммарное изменение формы (сумму квадратов отклонений точек эллипсоида от эквивалентной по объему сферы). Третий инвариант, например параметр Лодэ
 (12.49)
(12.49)
показывает особенности формы эллипсоида: если 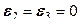 (осевое растяжение), то
(осевое растяжение), то 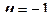 ; если
; если 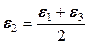 (кручение), то
(кручение), то  ; если
; если 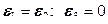 (двухосное растяжение), то
(двухосное растяжение), то 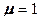 .
.
Деформированное состояние можно изобразить в виде кругов Мора (рис. 12.17). Значение первого инварианта (объемной деформации) отображает расположение кругов на оси 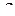 ; значение второго (интенсивности деформации) – радиус большого круга, значение третьего (параметра Лодэ
; значение второго (интенсивности деформации) – радиус большого круга, значение третьего (параметра Лодэ 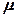 ) - соотношение размеров малых кругов.
) - соотношение размеров малых кругов.

Рис. 12.17. Круги Мора для линейных и угловых деформаций ( – угол между главной осью и осью координат; заштрихована область возможных сочетания линейных и угловых деформаций при различной ориентации осей координат)
– угол между главной осью и осью координат; заштрихована область возможных сочетания линейных и угловых деформаций при различной ориентации осей координат)
Теория напряжений
Механическим напряжением σ называется отношение силы P, действующей между двумя частями твердого тела, к площади A разделяющей их поверхности (рис. 12.18):
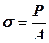 . (12.50)
. (12.50)
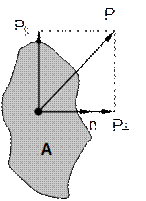
Рис. 12.18. Схема определения нормального и касательного напряжений
По размерности напряжение аналогично давлению и измеряется в мегапаскалях: 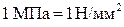 .
.
Если поверхность плоская, а сила перпендикулярна плоскости (действует по нормали к ней), напряжение называется нормальным:
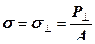 ,
,
а если сила действует вдоль плоскости (по касательной), напряжение называется касательным:
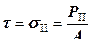 .
.
Нормальная сила аналогична силе давления, а касательная – силе трения. В общем случае сила P направлена под углом к поверхности и может быть разложена на составляющие 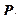 и
и 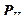 . Напряженное состояние в элементарном объеме характеризуют компоненты напряжения на трех секущих поверхностях, перпендикулярных осям координат. Силу, передаваемую через поверхность, можно разложить по осям координат и найти для каждого сечения три компоненты напряжения: нормальную и две касательных. Для обозначения компоненты используют два индекса, один из которых обозначает ось, нормальную к поверхности, а другой – ось, по которой действует составляющая силы. В тензорной записи оси обозначают номерами 1, 2 и 3, нормальные компоненты
. Напряженное состояние в элементарном объеме характеризуют компоненты напряжения на трех секущих поверхностях, перпендикулярных осям координат. Силу, передаваемую через поверхность, можно разложить по осям координат и найти для каждого сечения три компоненты напряжения: нормальную и две касательных. Для обозначения компоненты используют два индекса, один из которых обозначает ось, нормальную к поверхности, а другой – ось, по которой действует составляющая силы. В тензорной записи оси обозначают номерами 1, 2 и 3, нормальные компоненты 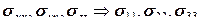 , а касательные компоненты
, а касательные компоненты 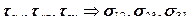 . Общая формула
. Общая формула
 . (12.51)
. (12.51)
Компоненты образуют тензор
 . (12.52)
. (12.52)
Формула (12.51) дает среднее напряжение на площадке 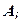 ; на бесконечно малой площадке (в точке)
; на бесконечно малой площадке (в точке)  .
.
Напряженное состояние в элементарном объеме изображают в виде кубика, на гранях которого стрелками показаны все компоненты тензора деформаций (рис. 12.19). По условиям равновесия этого кубика, в однородном поле напряжений одноименные компоненты напряжения на противоположных гранях равны и противоположно направлены. Касательные напряжения на противоположных гранях дают пары сил, создающие моменты. По условию равновесия, эти моменты должны быть уравновешены относительно каждой оси. Отсюда следует закон парности касательных напряжений:
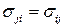 (12.53)
(12.53)
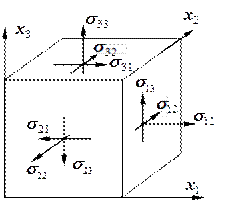
Рис. 12.19. Изображение компонент тензора напряжения
Тензор напряжения можно разделить на две составляющие: шаровой тензор 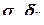 и девиатор
и девиатор 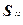 :
:
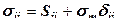 ; (12.54)
; (12.54)
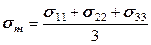 (12.55)
(12.55)
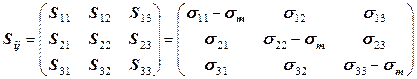 ; (12.56)
; (12.56)
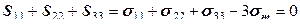 . (12.57)
. (12.57)
Изменение размеров при деформации сказывается на напряжениях. Напряжение называют условным при делении силы на начальное значение площади сечения и истинным - при делении силы на текущее значение (с учетом деформаций).
Главные напряжения  , а также коэффициенты кубического уравнения для их определения
, а также коэффициенты кубического уравнения для их определения
 : (12.58)
: (12.58)
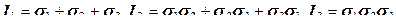
являются инвариантами тензора напряжений.
Наиболее важный физический смысл имеют два инварианта: среднее (гидростатическое) напряжение 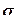 и интенсивность напряжения (инвариант девиатора)
и интенсивность напряжения (инвариант девиатора)
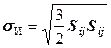 . (12.59)
. (12.59)
Первый из них выражает фактор напряженного состояния, изменяющий объем данного фрагмента тела, а второй пропорционален сумме квадратов всех компонент девиатора, т. е. суммирует (независимо от знака) все компоненты напряжения, вызывающие изменения формы. Их отношение
 (12.60)
(12.60)
называется показателем объемности напряженного состояния.
Если девиатор представить себе как вектор с компонентами 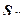 в многомерном пространстве, то
в многомерном пространстве, то 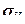 отражает длину (модуль) этого вектора. Коэффициент
отражает длину (модуль) этого вектора. Коэффициент 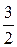 подобран так, чтобы в простейшем случае одноосного растяжения, когда все компоненты, кроме
подобран так, чтобы в простейшем случае одноосного растяжения, когда все компоненты, кроме 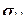 , равны нулю, получить
, равны нулю, получить 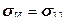 .
.
В сопротивлении материалов 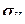 обычно используют в качестве эквивалентного напряжения
обычно используют в качестве эквивалентного напряжения  при различных схемах НДС. Например, при действии растяжения и сдвига
при различных схемах НДС. Например, при действии растяжения и сдвига  .
.
Аналогично в формуле (12.48) множитель подобран так, чтобы при одноосном пластическом растяжении, когда изменением объема можно пренебречь (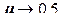 ;
;  ), получить
), получить  .
.
Главные напряжения и деформации часто бывают нужны. Например, если требуется найти истинные деформации, то для их линейных компонент имеется достаточно простая формула (12.36), а для сдвиговых компонент (при 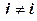 ) формулы гораздо сложнее. Поэтому рассчитывают все компоненты деформации Коши, затем переходят к главным осям этих деформаций, по формуле (12.36) рассчитывают главные истинные деформации в этих же осях, а затем возвращаются к исходной системе координат.
) формулы гораздо сложнее. Поэтому рассчитывают все компоненты деформации Коши, затем переходят к главным осям этих деформаций, по формуле (12.36) рассчитывают главные истинные деформации в этих же осях, а затем возвращаются к исходной системе координат.
Для нахождения компонент тензора напряжения в других осях координат используют уравнения равновесия клина (рис. 12.20):
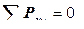 :
:
 ;
;
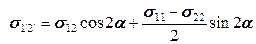 ;
;
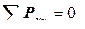 :
:
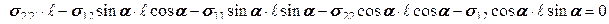
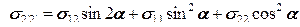 .
.
При  ; при
; при 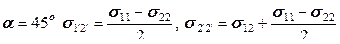 ;
;
при 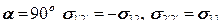 .
.
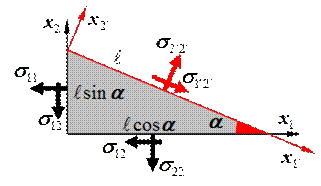
Рис. 12.20. Определение компонент напряжения в другой системе координат
 2020-10-10
2020-10-10 201
201








