Объемные графики строит функция ezsurf(функция, Хmin, Xmax, Ymin, Ymax) где по умолчанию переменные ограничены от 0 до 2π.
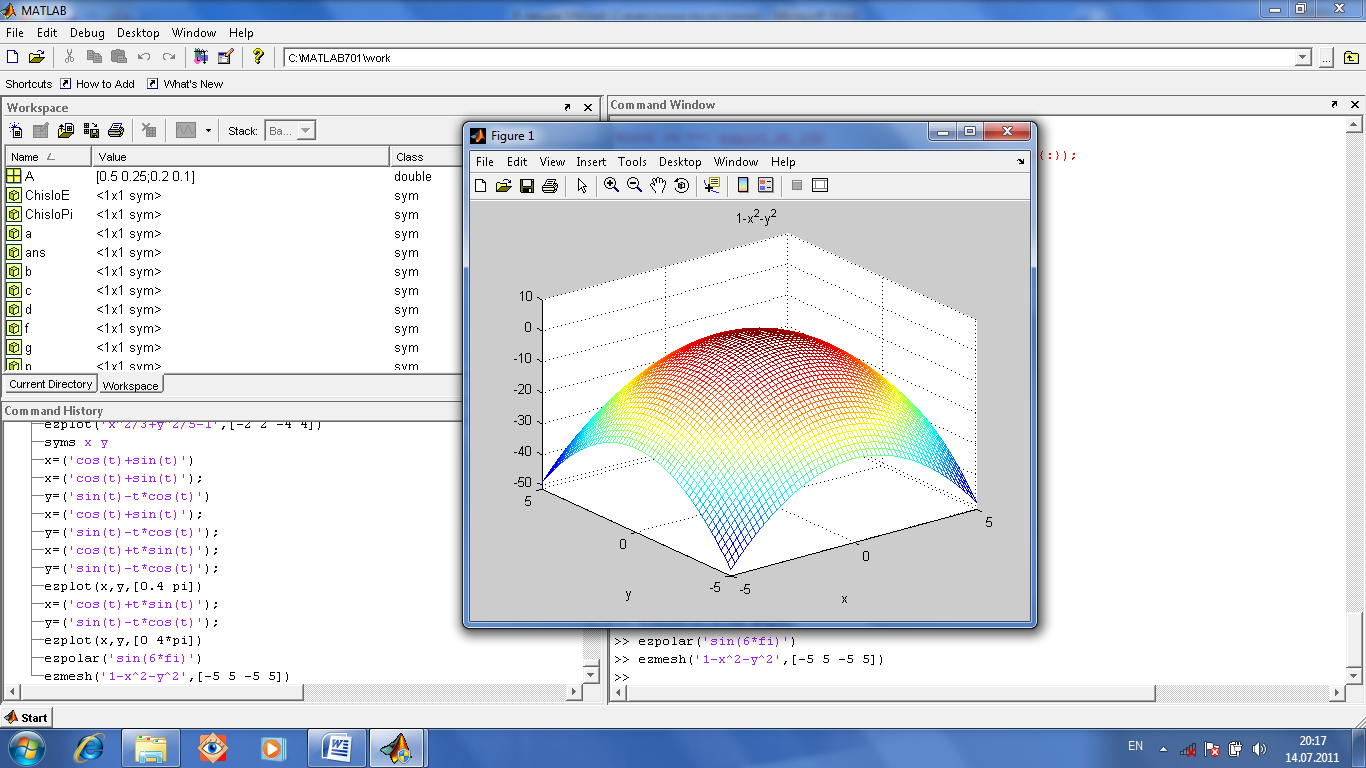
Если нужно показать еще и линии уровня, то можно использовать функцию ezsurfc. Если надо нанести контурные линии, то можно (рис.1.59) использовать ezmesh.
|
Рис.1.59. Объемный график символьной функции ezmesh('1-x^2-y^2',[-5 5 -5 5])
А если надо строить поверхность с нанесением контуров и линиями уровня, то можно использовать ezmeshc.
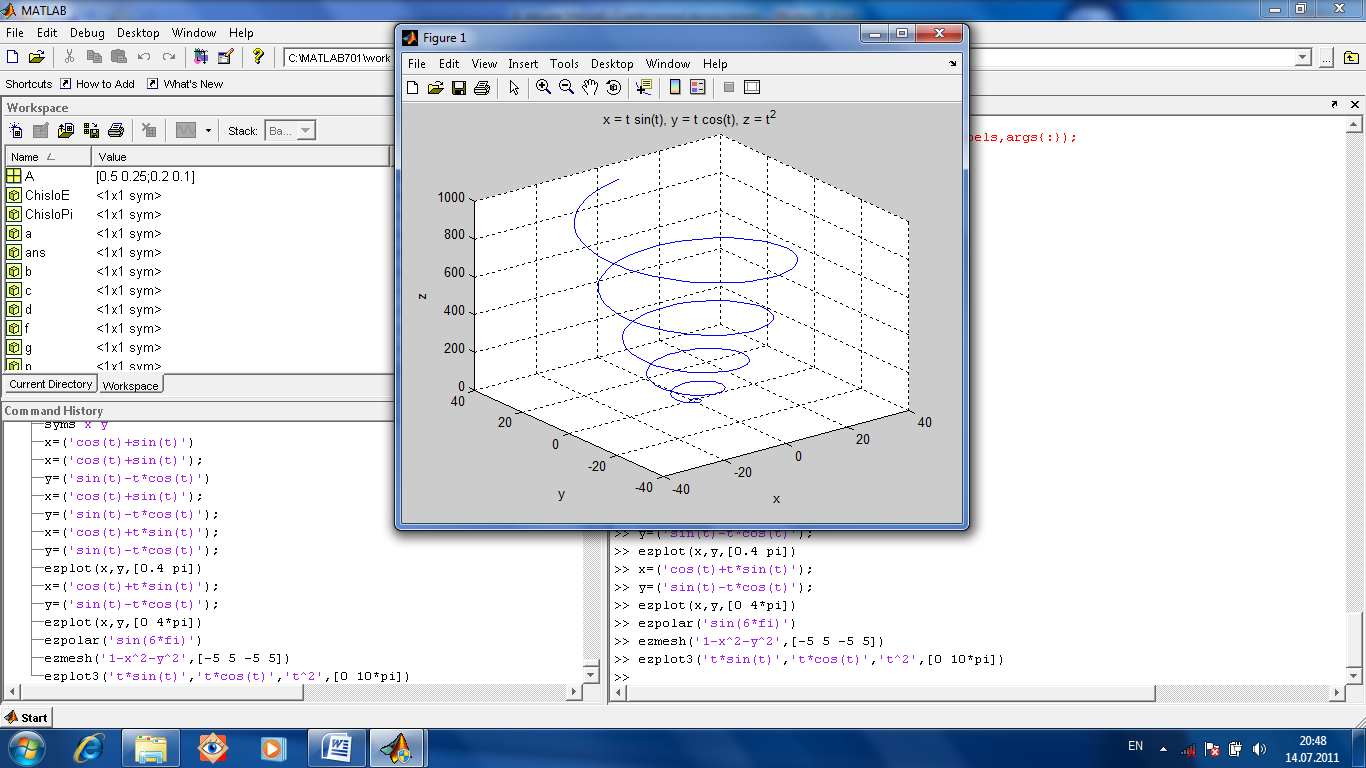
Для построения поверхности, заданной функциями в параметрическом виде (рис.1.60), используется ezplot3(X,Y,Z, [Tmin,Tmax]), где указаны аргументы (зависящие от параметра) и границы изменения параметра. По умолчанию параметр изменяется от 0 до 2π. Аргументы можно указывать как символьные выражения.
|
Рис.1.60. График поверхности, ezplot3('t*sin(t)','t*cos(t)','t^2',[0 10*pi])
Решение уравнений и систем в символьном виде. Функция solve(уравнение1, уравнение2, и т.д., переменнаяХ1, переменнаяХ2, и т.д.) возвращает значения переменных, перечисленных в ее аргументах, при которых соблюдаются равенства, заданные уравнениями, перечисленными в ее аргументах. Если же вычислить значение переменной не удалось, то она будет выражена через остальные переменные.
| >> syms x >> solve(x^5-x^3+1, x) ans = .95904771789275592744010129430222+.4283659562541893163489787094*i .34079486619700641527131389381414+.7854231030494490805285528960*i -1.2365057033914990243375748009761 -.34079486619700641527131389381414-.785423103049449080528552896*i .95904771789275592744010129430222-.428365956254189316348978709*i |
Или, например, с несколькими переменными, или тригонометрическая функция.
| >> syms a b c >> y=solve(a*x^2+b*x+c, x) y = 1/2/a*(-b+(b^2-4*a*c)^(1/2)) 1/2/a*(-b-(b^2-4*a*c)^(1/2)) | >> f=sym('sin(x)^2-x/2'); >> y=solve(f,x) y = 0 |
Для примера найдем уравнение окружности, проходящей через точки М(26, 4), О(9, 21), К(17, 17). Для этого составим систему из трех уравнений окружности, в каждое из которых подставлены координаты одной из точек. Решим его функцией solve и затем сформируем уравнение окружности (ответ нашей задачи) с помощью функции simplify, которая подставит найденные корни уравнения на соответствующие места в формуле. Функцию solve удобно применять для решения систем уравнений. После нахождения корней уравнений, удобно применить функцию simplify. Она подставит на место соответствующих переменных их вычисленные значения.
| function Start_sym5 syms x0 y0 R f1=sym('(26-x0)^2+(4-y0)^2-R^2'); f2=sym('(9-x0)^2+(21-y0)^2-R^2'); f3=sym('(17-x0)^2+(17-y0)^2-R^2'); [R,x0,y0]=solve(f1,f2,f3,x0,y0,R) syms xx yy RR F=simplify(subs('(x-xx)^2+(y-yy)^2-RR^2',{xx yy RR},{x0(1) y0(1) R(1)})) end | R = 25 -25 x0 = 2 2 y0 = -3 -3 F = x^2-4*x-612+y^2+6*y |
Вычисление пределов. Для вычисления пределов при числе членов последовательности, стремящемся к бесконечности, есть функция limit(функция, имяПеременной, пределПоследовательности). Так, например, выражение limit(f1,’n’,inf) это поиск предела последовательности при n стремящемся к бесконечности.
| function Start_sym6 f1=sym('((n+1)^3-(n-1)^3)/((n+1)^2+(n-1)^2)'); a1=limit(f1,'n',inf) end | a1= 3 |
Отдельно рассматривается ее применение для нахождения пределов функций. Так, например, выражение limit(f,’x’,3) означает что найден предел функции при Х стремящемся к 3. А вот выражение limit(1+1/x,x,inf) означает что найден предел функции при Х стремящемся к бесконечности.
Совершенно так же решаются и все неопределенности. Если же надо найти односторонний предел, то пишут с какой стороны его искать (справа или слева).
| function Start_sym7 f=sym('2^(1/(x^2-4))'); a1= limit(f,x,2,'right') a2= limit(f,x,2,'left') f=sym('3*x+1'); a3= limit(f,'x',3) syms x a4= limit(1+1/x,x,inf) end | a1 = Inf a2 = 0 a3 = 10 a4 = 1 |
Вычисление производной. Символьное дифференцирование выполняет команда diff(функция, имяПеременной, порядокПроизводной).
Если нет имени, то по умолчанию будет выбрана первая по алфавиту переменная. По умолчанию вычисляется первая производная.
Подставить значение переменной в найденную формулу производной можно с помощью subs(функция, имяПеременной, ееЗначение).
| function Start_Sym8 g=diff('5*(sin(x)^2)',x,1) a1= subs(g,x,pi/4) end | a1 = 5 g = 10*sin(x)*cos(x) |
Вычисление интеграла. Для неопределенного интеграла есть функция int(функция, переменная). Для определенного интеграла еще приписывают пределы интегрирования в список аргументов.
Для несобственного интеграла один из пределов равен бесконечности.
| function Start_Sym9 a1=int('cos(x)',x) f=sym('(sin(x)^2)/(cos(x)+5)'); a2=int(f,x,0,pi) a3= int('1/(x^2)',x,1,inf) end | a1 = sin(x) a2 = 5*pi-2*6^(1/2)*pi a3 = 1 |
Числовые ряды. Ряд Тейлора. Для вычисления суммы ряда есть функция symsum(общийЧленРяда, переменная, пределыЕеИзменения).
| function Start_Sym10 f=sym('1/(n^2)'); a1= symsum(f,'n',1,inf) end | a1 = 1/6*pi^2 |
Для разложения в ряд Тейлора (ряд Маклорена его частный случай) есть функция taylor(функция, номер), где номер означает, до какого члена ряда выполняется разложение. По умолчанию до шестого члена ряда.
Если же надо разложить в ряд Тейлора в окрестности точки А, то ее надо указать в списке аргументов taylor(функция, точкаА, номер).
| function Start_Sym11 g=taylor(exp(x),'a',3) a1=subs(g,a,4) end | g = exp(a)+exp(a)*(x-a)+1/2*exp(a)*(x-a)^2 a1 = exp(4)+exp(4)*(x-4)+1/2*exp(4)*(x-4)^2 |
Дифференциальные уравнения. Их и их системы решает функция dsolve(список уравнений, список граничных (начальных) условий, независимая переменная).
По умолчанию имя переменной считается t. Имя переменной нельзя начинать с D или d так как это означает производную.
| function Start_Sym12 a1=dsolve('Dy-y/(1-x^2)=1+x','y(0)=1','x') a2= dsolve('D2y=x*Dy+y+1') [x,y]=dsolve('D2y=x','D2x=y') a3=dsolve('Dy=(y+1)/x') end | a1 = (1/2*x*(1-x^2)^(1/2)+1/2*asin(x)+1) *(1+x)/(1-x^2)^(1/2) a2 = exp((1/2*x+1/2*(x^2+4)^(1/2))*t)*C2+exp((1/2*x-1/2*(x^2+4)^(1/2))*t)*C1-1 x = C1*exp(-t)+C2*exp(t)-C3*sin(t)-C4*cos(t) y = C1*exp(-t)+C2*exp(t)+C3*sin(t)+C4*cos(t) a3 = -1+exp(1/x*t)*C1 |
 2020-10-10
2020-10-10 177
177








